pytorch自动求梯度
自动求梯度
在深度学习中,我们经常需要对函数求梯度(gradient)。PyTorch提供的autograd包能够根据输入和前向传播过程自动构建计算图,并执行反向传播。本节将介绍如何使用autograd包来进行自动求梯度的有关操作。
1.1 概念
上一节介绍的Tensor是这个包的核心类,如果将其属性.requires_grad设置为True,它将开始追踪(track)在其上的所有操作(这样就可以利用链式法则进行梯度传播了)。完成计算后,可以调用.backward()来完成所有梯度计算。此Tensor的梯度将累积到.grad属性中。
注意在y.backward()时,如果y是标量,则不需要为backward()传入任何参数;否则,需要传入一个与y同形的Tensor。
1.2 Tensor
创建一个 Tensor 并设置 requires_grad=True
import torch
x = torch.ones(2,2,requires_grad = True)
print(x)
print(x.grad_fn)
输出
tensor([[1., 1.],
[1., 1.]], requires_grad=True)
None
再做一下运算操作:
y = x + 2
print(y)
print(y.grad_fn)
输出结果
tensor([[3., 3.],
[3., 3.]], grad_fn=<AddBackward>)
<AddBackward object at 0x1100477b8>
注意x是直接创建的,所以它没有grad_fn, 而y是通过一个加法操作创建的,所以它有一个为的grad_fn。
像x这种直接创建的称为叶子节点,叶子节点对应的grad_fn是None。
print(x.is_leaf,y.is_leaf)
# True False
再来点复杂度运算操作:
z = y * y * 3
out = z.mean()
print(z,out)
输出结果:
tensor([[27., 27.],
[27., 27.]], grad_fn=<MulBackward0>) tensor(27., grad_fn=<MeanBackward0>)
通过 .requires_grad_() 来用in-place的方式改变requires_grad属性
a = torch.randn(2,2) # 缺失情况下默认requires_grad = False
a = ((a*3)/(a-1))
print(a.requires_grad) # False
a.requires_grad_(True)
print(a.requires_grad) # True
b = (a * a).sum()
print(b.grad_fn) # 1.3 梯度
因为out是一个标量,所以调用backward()时不需要指定求导变量
out.backward() # 等价于out.backward(torch.tensor(1.))
print(x.grad)
#tensor([[4.5000, 4.5000],
# [4.5000, 4.5000]])
# 再来反向传播一次,注意grad是累加的
out2 = x.sum()
out2.backward()
print(x.grad)
out3 = x.sum()
x.grad.data.zero_()
out3.backward()
print(x.grad)
输出结果:
tensor([[5.5000, 5.5000],
[5.5000, 5.5000]])
tensor([[1., 1.],
[1., 1.]])
为什么在y.backward()时,如果y是标量,则不需要为backward()传入任何参数;否则,需要传入一个与y同形的Tensor? 简单来说就是为了避免向量(甚至更高维张量)对张量求导,而转换成标量对张量求导。举个例子,假设形状为 m x n 的矩阵 X 经过运算得到了 p x q 的矩阵 Y,Y 又经过运算得到了 s x t 的矩阵 Z。那么按照前面讲的规则,dZ/dY 应该是一个 s x t x p x q 四维张量,dY/dX 是一个 p x q x m x n的四维张量。问题来了,怎样反向传播?怎样将两个四维张量相乘???这要怎么乘???就算能解决两个四维张量怎么乘的问题,四维和三维的张量又怎么乘?导数的导数又怎么求,这一连串的问题,感觉要疯掉…… 为了避免这个问题,我们**不允许张量对张量求导,只允许标量对张量求导,求导结果是和自变量同形的张量。**所以必要时我们要把张量通过将所有张量的元素加权求和的方式转换为标量,举个例子,假设y由自变量x计算而来,w是和y同形的张量,则y.backward(w)的含义是:先计算l = torch.sum(y * w),则l是个标量,然后求l对自变量x的导数。
x = torch.tensor([1.0, 2.0, 3.0, 4.0], requires_grad=True)
y = 2 * x
z = y.view(2, 2)
print(z)
输出结果
tensor([[2., 4.],
[6., 8.]], grad_fn=<ViewBackward>)
现在 z 不是一个标量,所以在调用backward时需要传入一个和z同形的权重向量进行加权求和得到一个标量。
v = torch.tensor([[1.0, 0.1], [0.01, 0.001]], dtype=torch.float)
z.backward(v)
print(x.grad)
# tensor([2.0000, 0.2000, 0.0200, 0.0020])
注意,x.grad 是和 x 同形的张量。
再来看看中断梯度追踪的例子:
x = torch.tensor(1.0,requires_grad = True)
y1 = x ** 2
with torch.no_grad():
y2 = x ** 3
y3 = y1 + y2
print(x.requires_grad)
print(y1,y1.requires_grad)
print(y2,y2.requires_grad)
print(y3,y3.requires_grad)
输出结果:
True
tensor(1., grad_fn=<PowBackward0>) True
tensor(1.) False
tensor(2., grad_fn=<AddBackward0>) True
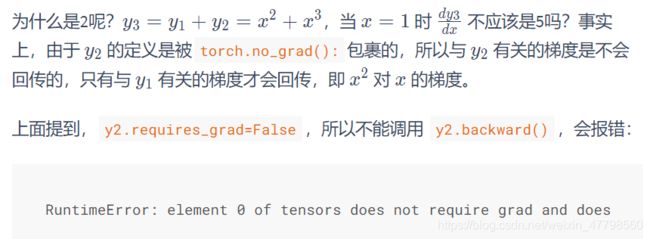
可以看到,上面的y2是没有grad_fn而且y2.requires_grad=False的,而y3是有grad_fn的。如果我们将y3对x求梯度的话会是多少呢?
y3.backward()
print(x.grad)
# tensor(2.)
此外,如果我们想要修改 tensor 的数值,但是又不希望被 autograd 记录(即不会影响反向传播),那么可以对 tensor.data 进行操作。
x = torch.ones(1,requires_grad = True)
print(x.data) # 还是一个tensor
print(x.data.requires_grad) # 但是已经是独立于计算图之外
y = 2 * x
x.data *= 100 # 只改变了值,不会记录在计算图,所以不会影响梯度传播
y.backward()
print(x) # 更改data的值也会影响tensor的值
print(x.grad)
输出结果:
tensor([1.])
False
tensor([100.], requires_grad=True)
tensor([2.])
练习
import numpy as np
from matplotlib import pyplot as plt
x = np.linspace(0,10,100)
x1 = torch.tensor(x,requires_grad = True,dtype=torch.float)
y1 = torch.sin(x1)
y1.sum().backward()
#print(x1.grad)
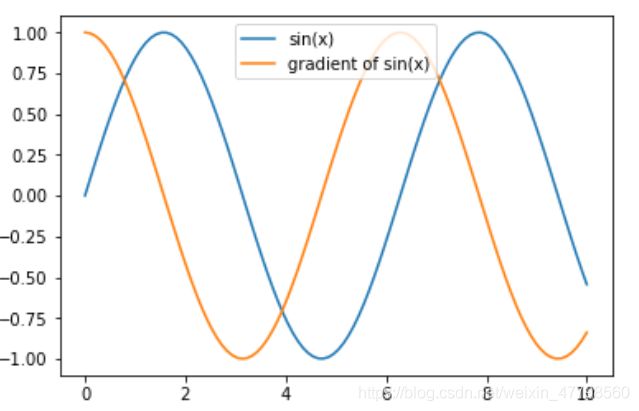
plt.plot(x,np.sin(x),label = 'sin(x)')
plt.plot(x,x1.grad,label = 'gradient of sin(x)')
plt.legend(loc = 'upper center')
plt.show()