【推荐系统多任务学习 MTL】PLE论文精读笔记（含代码实现）

论文地址：

1. Progressive Layered Extraction (PLE): A Novel Multi-Task Learning (MTL) Model for Personalized Recommendations

前言

PLE 为 Recsys 2020最佳长论文，出自腾讯的 PCG（Platform and Content Group） 推荐视频团队。PLE 是 MMoE （详见【推荐系统多任务学习MTL】MMOE论文精读笔记（含代码实现）
）的改进版，结构简单且效果好，PLE 主要是在 MMoE 的基础上，为每个任务增加了自己的 specific expert，仅由本任务对其梯度更新。

一、背景

多任务学习（multi-task learning，MTL）在推荐系统中已经有很多成功的应用，但是存在部分问题没有解决的很好。其中一个为负迁移（negative transfer），推荐系统中的任务通常是低相关甚至是相互冲突的，联合训练可能导致性能下降，称之为负迁移。

另一个是跷跷板现象（seesaw phenomenon），在全部任务中超越单任务模型是非常困难的，即使是一些很新的SOTA的模型在大量的实验中也没有处理好这个问题。当任务之间出现比较复杂的关系或者有样本之间的依赖关系时。目前的MTL模型很难同时在所有任务上超过single-task模型。

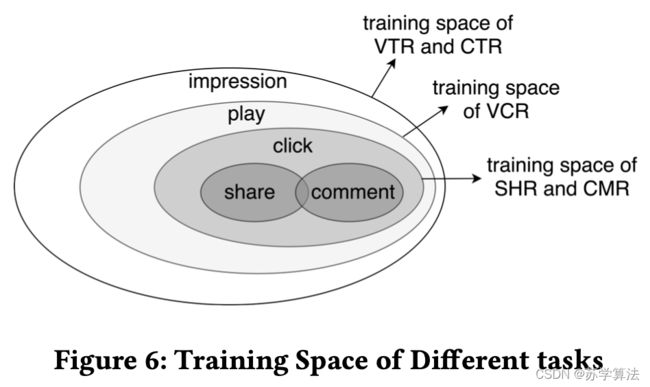
腾讯新闻的 MTL ranking system 简介：这是一个根据用户反馈进行 news 和 videos 推荐的内容平台。建模的目标包含用户的多种不同的行为：点击，分享，评论等等。每次请求，候选的排序分根据下面的公式计算：
$$score=p{VTR}^{wVTR}\times p{VCR}^{wVCR}\times p{SHR}^{wSHR}\times \dots \times p_{CMR}^{wCMR}\times f\left(vide{o}_{-}len\right)$$
其中，$w$ 表示每个预估行为的相对重要性，$f(vedi{o}_{l}en)$ 是一个非线性函数，例如 sigmoid、log 函数等。VTR（View- Through Rate）表示有效观看率，VCR（View Completion Ratio）表示完播率，SHR（Share Rate）表示分享率，CMR（Comment Rate）表示评论率。

其中 VTR 和 VCR 是最重要的两个在线指标，分别代表了 view-count 和 watch time。VCR 是使用 MSE 损失训练的回归任务，用于预测每个视频的完播率。 VTR 是一种用交叉熵损失训练的二元分类任务，用于预测有效播放的概率（超过一定观看时间阈值的播放认为是有效播放）。

从 VTR 和 VCR 定义可以看出两者之间有比较复杂的关系：

• VTR的 label 和 播放动作（play action） & VCR 有关系，因为只有 play action 并且观看时长大于阈值视为有效观看。
• play action 的分布十分复杂，因为WIFI环境下自动播放的概率明显比较高，相对地，其他需要手动点击播放的场景play的概率较低。

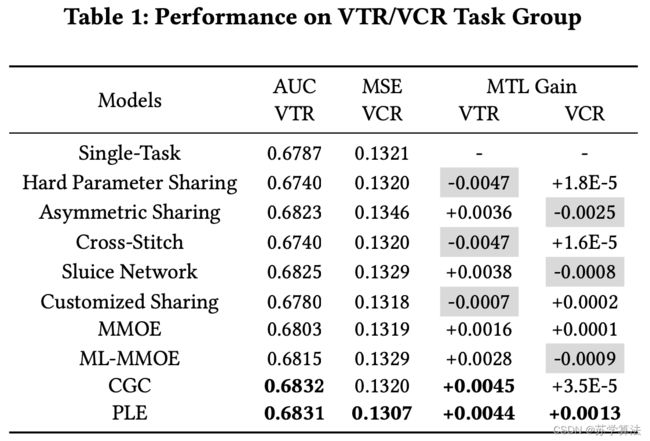
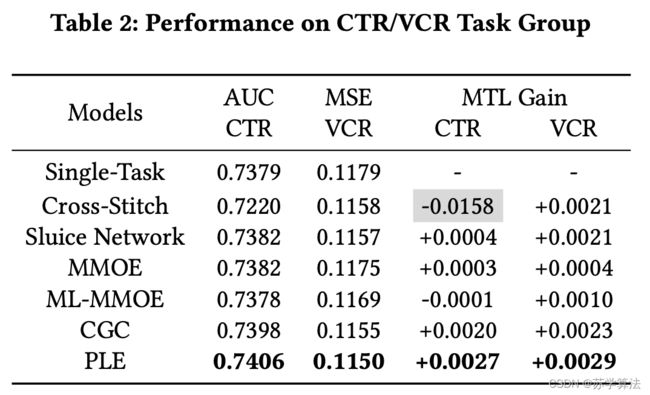
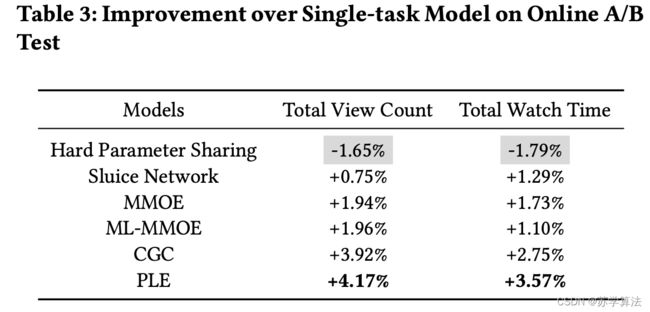
正因如此，同时对 VCR 和 VTR 进行建模使得“跷跷板现象”（seesaw phenomenon）比较明显。

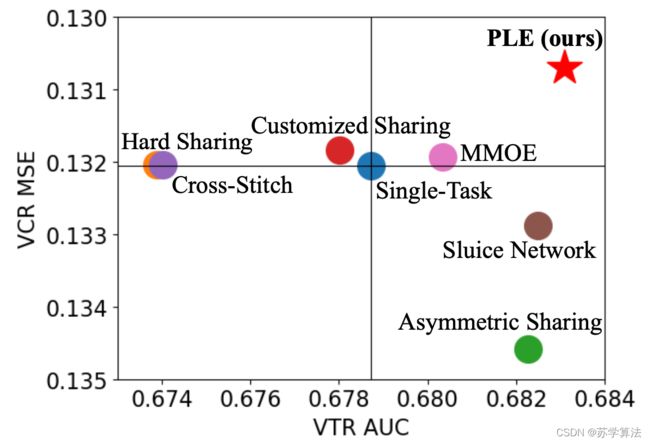
上图可以看出，以 single task 作为基线零点，同时在 VTR 和 VCR 两个任务中超过 single task 的只有 PLE，其他模型都有明显的跷跷板现象（或VTR比较差，或CVR比较差）

二、相关工作

Hard parameter sharing 是最简单的也是最容易受到 negative transfer 问题影响效果的MTL网络结构

在 MTL 中，前人做过很多工作用来处理 negative-transfer 问题，例如：cross-stitch network， sluice network 。用来学习如何把不同的 task 的 表达（representations） 线性地融合起来。 这里的组合方式是偏静态的方式，比如静态权重超参数。

但是这种将表达（representations）通过静态权重融合起来的方式并不合理，且跷跷板现象没有得到解决。

此外有一些利用门结构（gate structure）和注意力网络（attention network）来做信息融合的工作。关于门结构的使用，如 MMoE 模型。但是 MMoE 的所有 experts 会被上层不同的子任务共享，忽略了专家（experts）之间的差异（详见【推荐系统多任务学习MTL】MMOE论文精读笔记（含代码实现）。这一点作者已经证明了会造成跷跷板现象。本文的主要改动的 motivation 也来自于此。下面的右图是 multi-layer 的 MMoE

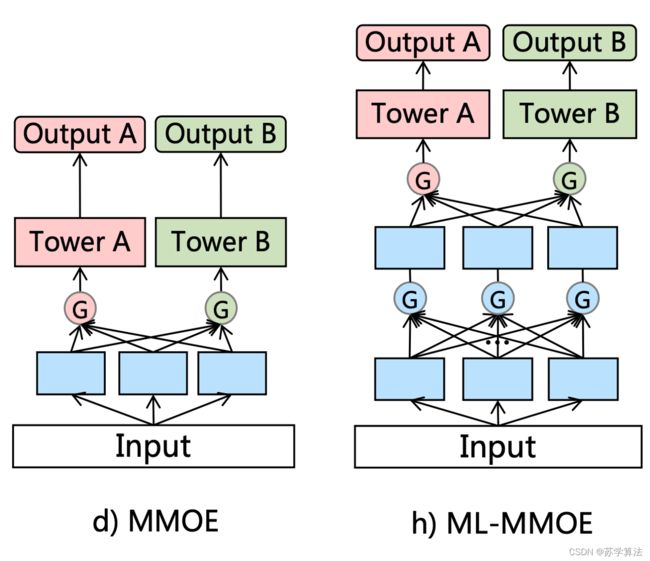
MRAN(Multiple Relational Attention Network for Multi-task Learning) 利用 multi-head self-attention 来学习不同 feature sets 的不同表达，不论是 MMOE 还是 MRAN 都没有task-specific 的概念，而是倾向于对所有信息做共享。

三、本文创新点

3.1 信息独享的其他方案

1. 非对称参数共享（Asymmetric Sharing）

下图是基于 hard-sharing 的非对称参数共享结构，有一部分信息可以被共享，另一部分信息被独享。其信息融合方式包括 concatenation，sum-polling，average-pooling

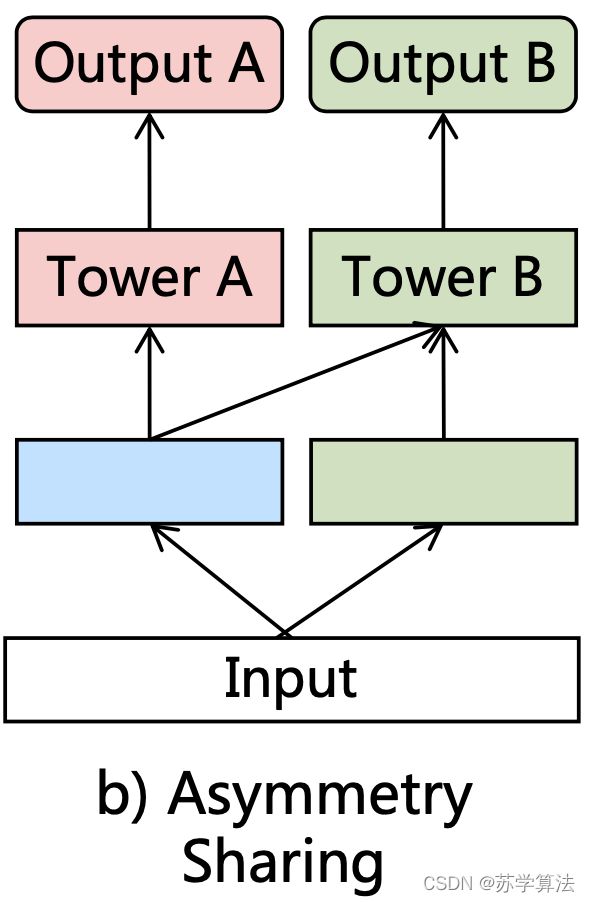
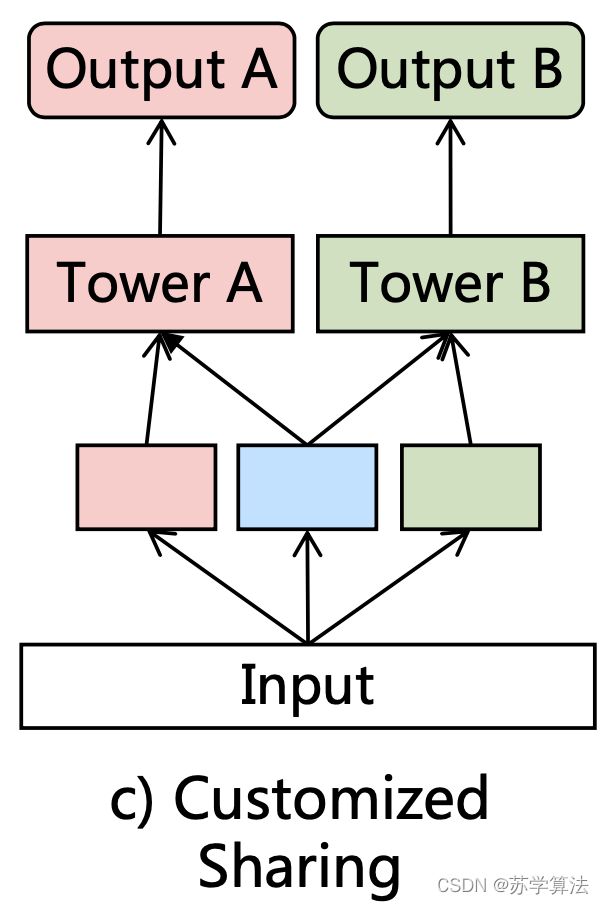
2. 定制分享（Customized Sharing）

下图的结构中，两个塔各自有一个独有的 expert，并且还有一个共享的 expert（浅蓝色）。显式分离 shared 和 task-specific 参数来避免可能存在的内在冲突和 negative transfer。对比 single-task 模型，增加了一个抽取共享信息的底层网络，并和 task-specific 层 concat 起来输入到各自的 tower layer

3.2 定制门控网络 （Customized Gate Control, CGC）

CGC 是 PLE 的基础网络。CGC 和上面的 Customized Sharing 网络的区别在于增加了一个门控网络，相似点在于也将 task-common 和 task-specific 分离。由第一节的“跷跷板现象”图中可以看到，Customized Sharing 网络的结果和 Single Task 很相近，因此可以使用 Customized Sharing 作为基础结构，以便于体现后面提到的 Task-specific 的作用。

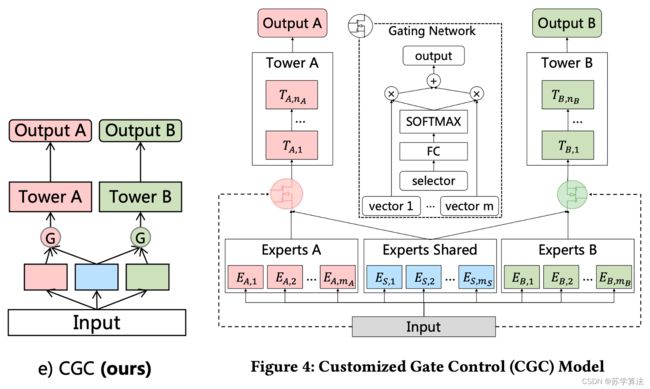
• 底层网络：包含一些 expert 模块, 每个expert 模块由若干子网络(sub-networks)构成，这些子网络称作 experts，每个模块包含多少个 expert 是可调节的超参。其中 shared experts 负责学习 shared patterns，task-specific experts负责学习task-specific patterns。
• 上层网络：一些 task-specific 塔 ，网络的宽度和深度都是可调节的超参。每个塔同时从 shared experts 和各自的task-specific experts 中学习知识。
• 门控网络：Shared experts 和 task-specific experts 的信息通过门控网络进行融合。门控网络的结构为单层的前向网络，激活函数为softmax 函数。

第 $k$ 个子任务的门控网络输出为：
$$g^k(x)=w^k(x)S^k(x)$$
其中 $x$ 是输入的向量表达（representations），$w^k(x)=\mathrm{softmax}\left(W_g^{k}x\right),W_g^k\in R^{\left(m_k+m_s\right)\times d}$

$S^k(x)$ 是一个选择矩阵，把 shared experts 和第 $k$ 个子任务的 specific experts 串接（concat）起来。
$$S^k(x)={\left[E_{(k,1)}^T,E_{(k,2)}^T,\dots \dots ,E_{\left(k,m_k\right)}^T,E_{(s,1)}^T,E_{(s,2)}^T,\dots \dots ,E_{\left(s,m_s\right)}^T\right]}^T$$

最终第 $k$ 个子任务的预估值为
$$y^k(x)=t^k\left(g^k(x)\right)$$
其中，$t^k$ 表示第 $k$ 个子任务的上层塔网络。

对比 MMoE，CGC 去掉了子任务塔和其他 task-specific experts 的连接，这就使得不同类型 experts 可以专注于更高效地学习不同的知识且避免不必要的交互。另外，得益于门控网络动态地融合输入，CGC可以更灵活地在不同子任务之间找到平衡且更好地处理任务之间的冲突和样本相关性问题（即前面提到的 VCR 和 VCR 的复杂关联）。

3.3 PLE(Progressive Layer Extraction)

PLE是CGC的一个多层拓展，还利用了一个新颖的 progressive seperation routing 机制。

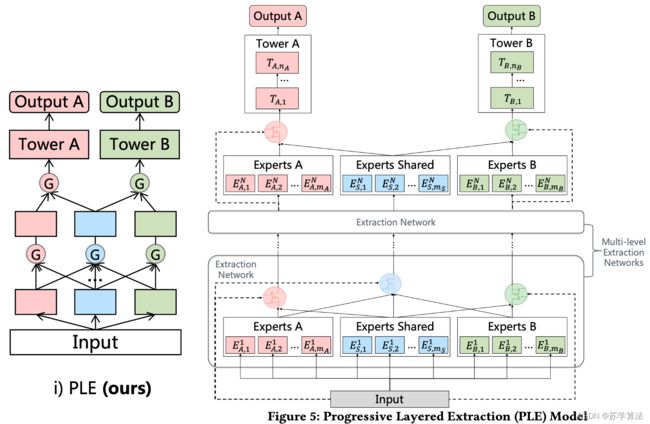
众所周知，越深的 MTL 网络可以渐进地学到更深的语义表达，一开始也不知道当前的特征表达应该作为 shared 还是 task-specific。于是CGC就扩展成了PLE，PLE利用多层网络抽取高阶的共享信息。除了 task-specific experts 有门控网络，抽取网络也对当前层所有的 experts 利用门控网络来融合得到新的 shared experts。因此，PLE的 early 层没有完全把子任务的参数区分开，而是在 upper 层逐渐地分离。底层的抽取网络对于高层的抽取网络来说，是代替CGC中原始输入的存在，而这个替代可以带来更多的信息有助于更高层网络的学习。

PLE 的第 $k$ 个子任务的第 $j$ 个提取网络中门控网络的定义：
$$g^{k,j}(x)=w^{k,j}\left(g^{k,j-1}(x)\right)S^{k,j}(x)$$
计算完所有的门控网络和 experts，PLE的第 $k$ 个子任务的最终输出为
$$y^k(x)=t^k\left(g^{k,N}(x)\right)$$

正因为有了多层的 experts 和 gating networks，PLE 可以抽取并融合每个子任务更深的表达来提升泛化性。

Routing 策略在 MMoE 中是全连接层，在 CGC 中是 early separation。PLE采用一种渐进式分离 routing 的方案来从所有的底层 experts 中获取信息，抽取成高阶的共享知识，并逐渐分离 task-specific 参数。

3.4 损失函数

一般来说，MTL 的损失函数的设计方式是，针对不同的子任务，设置不同的权重，而后再把所有子任务的损失按照权重加权得到。
$$L\left({\theta }_1,\dots \dots ,{\theta }_K,{\theta }_s\right)=\sum _{k=1}^K{\omega }_k{L}_k\left({\theta }_k,{\theta }_s\right)$$
其中，${\theta }_s$ 表示共享参数（shared parameters），$K$ 是子任务的个数。$L_k,{\omega }_k,{\theta }_k$ 分别表示第 $k$ 个任务的损失函数、损失函数的权重、task-specific 的参数。

但是在本场景中，采用这样的损失函数会存在问题，原因如下

• 解决样本空间不一致的问题。用户的行为有序列性导致样本空间是异构的（如上图，不同任务的样本空间不同），比如用户只有点击后才能进行分享和评论。解决样本空间不一致的问题，前面我们介绍过 ESMM 的方式（详见【推荐系统多任务学习MTL】ESSM 论文精读笔记（含代码实现））。而本文则是在 Loss 上进行一定的优化，联合训练这些任务，在计算每个任务的损失时需要把样本空间相同的合并，并忽略不在自己样本空间的样本，即不同的任务仍使用其各自样本空间中的样本。
  $$L_k\left({\theta }_k,{\theta }_s\right)=\frac{1}{{\sum }_i{\delta }_k^i}\sum _i{\delta }_k^i{\mathrm{loss}}_k\left({\hat{y}}_k^i\left({\theta }_k,{\theta }_s\right),y_k^i\right)$$
  其中 ${\delta }_k^i$ 取值为 0 或 1，表示第 $i$ 个样本是否属于第 $k$ 个任务的样本空间。

• 其次是不同任务之间权重的优化。MTL 模型的效果在训练过程中对损失的权重（loss weight）的选择敏感。不同子任务可能在不同的训练阶段有不同的重要性。关于MTL的权重设置，最常见的是人工设置，这需要不断的尝试来探索最优的权重组合，另一种则是阿里提出的通过帕累托最优来计算优化不同任务的权重。本文则使用动态调整的方式，首先对第 $k$ 个子任务设置一个初始值，之后每一步根据跟新率（updating ratio）${\gamma }_k$ 更新它的损失的权重（loss weight）
  $${\omega }_k^{(t)}={\omega }_{k,0}\times {\gamma }_k^t$$
  其中 $t$ 表示训练的 epoch，其他两个都是超参

四、实验结果

4.1 腾讯视频推荐数据集

数据集介绍：从线上抽取连续8天的用户行为日志，一共 46.926 百万用户，2.682 百万视频和9.95亿样本。建模的用户行为包括CTR，VCR，VTR，SHR，CMR

为了对比公平，作者也实现了multi-level 版的 MMOE

指标除了 AUC 和 MSE，还有个 MTL gain，定义如下
$$\text{ MTL gain }=\{\begin{array}{ll}{M}_{MTL}-M_{\text{single }},& M\text{ is a positive metric }\\ M_{\text{single }}-M_{MTL},& M\text{ is a negative metric }\end{array}$$

• 联合训练VTR和VCR任务（任务之间有复杂的联系）
  

• 联合训练CTR和VCR任务（任务之间是普通的联系）
  

• 线上AB实验的效果
  

• 联合训练三个以上任务的时候的效果
  

4.2 公开数据集

1. Synthetic Data:人工构造的数据集，参考 MMOE 论文，每个correlation构造了140万的两个连续label的样本
2. Census-income Dataset：从1994年人口普查数据库中抽取的299285个样本和40个特征，和MMOE论文中的实验一样，任务 1 预测人群中收入是否大于50k，任务 2 预测是否未婚
3. Ali-CCP Dataset：包含8.4千万个从淘宝推荐系统中抽取的样本。CTR和CVR是两个联合建模的任务
   
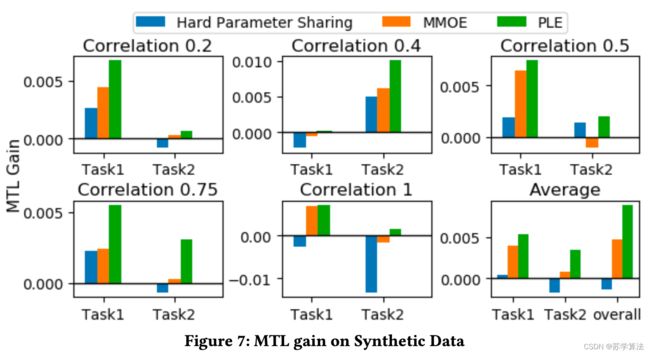
   Hard parameter sharing 和 MMOE 有时候遭遇跷跷板现象并在两个任务中失去平衡。PLE持续的表现最优，且相比 MMOE 平均在 MTL gain上提升87.2%
   
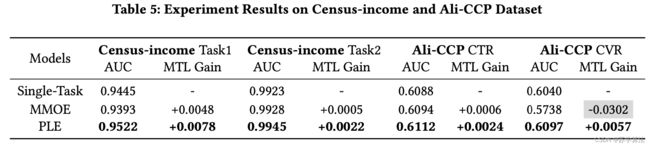
   在census-income和Ali-CCP数据集上，PLE都消除了跷跷板现象且相比 MMOE 和 single-task 都取得了最好的效果

4.3 Experts 利用率分析

为了探究不同的门如何聚合experts的信息，作者研究了建模VTR/VCR任务的模型中expert利用情况，为了实现方便和公平，每个expert都是一个一层网络，每个expert module都只有一个expert，每一层只有3个expert

柱子的高度和竖直短线分别表示权重的均值和方差。

可以看到，无论是 MMoE 还是 ML-MMoE，不同任务在三个 Expert 上的权重都是接近的，这其实更接近于一种 Hard Parameter Sharing 的方式，但对于 CGC & PLE 来说，不同任务在共享 Expert 上的权重是有较大差异的，其针对不同的任务，能够有效利用共享 Expert 和独有 Expert 的信息，这也解释了为什么其能够达到比 MMoE 更好的训练结果。

五、论文理解

PLE，主要是在MMoE的基础上，为每个任务增加了自己的specific expert，仅由本任务对其梯度更新。

在Share Bottom的结构中，整个共享参数矩阵如同质量较大的物体，在梯度更新的环节，两个loss反向计算的梯度向量分别是 $g_1$ 和 $g_2$，是这个物体受到的两个不同方向不同大小的力，这两个力同时来挪动这个物体的位置，如果在多次更新中两个力大概率方向一致，那么就能轻松达到和谐共存、相辅相成。反之，多个力可能出现彼此消耗、相互抵消，那么任务效果就会大打折扣。

MMoE 通过“化整为零”，把一个共享参数矩阵化成多个结合 gate 的共享 Expert，这样不同的 loss 在存在相互冲突的时候，在不同的expert上，不同loss可以有相对强弱的表达，那么出现相互抵消的情况就可能减少，呈现出部分 experts 受某子任务影响较大，部分 experts 受其他子任务主导，形成“各有所得”的状态。而 PLE 增加了spcific experts，能进一步保障“各有所得”，保证稳定优化。

六、代码实现

代码参考

1. github1
2. github2（浅梦学习笔记）5.9K star

PLE 的核心代码

class PleLayer(tf.keras.layers.Layer):
    '''
    @param n_experts: list,每个任务使用几个expert。[3,4]第一个任务使用3个expert，第二个任务使用4个expert。
    @param n_expert_share: int,共享的部分设置的expert个数。
    @param expert_dim: int,每个专家网络输出的向量维度。
    @param n_task: int,任务个数。
    '''
    def __init__(self,n_task,n_experts,expert_dim,n_expert_share,dnn_reg_l2 = 1e-5):
        super(PleLayer, self).__init__()
        self.n_task = n_task
        # 定义多个任务特定网络和1个共享网络
        self.E_layer = []
        for i in range(n_task):
            sub_exp = [Dense(expert_dim,activation = 'relu') for j in range(n_experts[i])]
            self.E_layer.append(sub_exp)
        self.share_layer = [Dense(expert_dim,activation = 'relu') for j in range(n_expert_share)]
        # 定义门控网络
        self.gate_layers = [Dense(n_expert_share+n_experts[i],kernel_regularizer=regularizers.l2(dnn_reg_l2),
                                  activation = 'softmax') for i in range(n_task)]
    def call(self,x):
        # 特定网络和共享网络
        E_net = [[expert(x) for expert in sub_expert] for sub_expert in self.E_layer]
        share_net = [expert(x) for expert in self.share_layer]
        # 【门权重】和【指定任务及共享任务输出】的乘法计算
        towers = []
        for i in range(self.n_task):
            g = self.gate_layers[i](x)
            g = tf.expand_dims(g,axis = -1) #维度 (bs,n_expert_share+n_experts[i],1)
            _e = share_net+E_net[i]  
            _e = Concatenate(axis = 1)([expert[:,tf.newaxis,:] for expert in _e]) #维度 (bs,n_expert_share+n_experts[i],expert_dim)
            _tower = tf.matmul(_e, g,transpose_a=True)
            towers.append(Flatten()(_tower)) #维度 (bs,expert_dim)
        return towers

参考：

1. Progressive Layered Extraction (PLE): A Novel Multi-Task Learning (MTL) Model for Personalized Recommendations
2. 大厂技术实现 | 多目标优化及应用（含代码实现）
3. 推荐系统遇上深度学习(九十二)-[腾讯]RecSys2020最佳长论文-多任务学习模型PLE