系统动力学学习日记

1. 系统动力学理论基本概念和构模主要过程与步骤

• 1.1 系统、模拟与模型

系统动力学中系统的定义：一个由相互区别、相互作用的诸元素有机地联结在一起，而具有某种功能的集合体。（系统为相互作用诸单元的复合体）

模拟是对真实客观事物内在结构及其运动、发展的动态行为的模仿。

系统动力学模型是按照系统动力学理论建立起来的数学模型，采用专用语言，借助数字计算机进行模拟分析研究，以处理行为随时间变化的复杂系统的问题。

• 1.2 反馈系统
• 1.2.1 定义

反馈是指信息的传输与回授。

反馈可以从单元或子块或系统的输出直接联至其相应的输入，也可以经由媒介——其他单元、子块，甚至其它系统实现。

• 1.2.2 反馈系统与反馈回路          

反馈系统是包含有反馈环节与其作用的系统。（闭环系统）

反馈回路是由一系列因果与相互作用链组成的闭合回路（由信息与动作构成的闭合路径）。

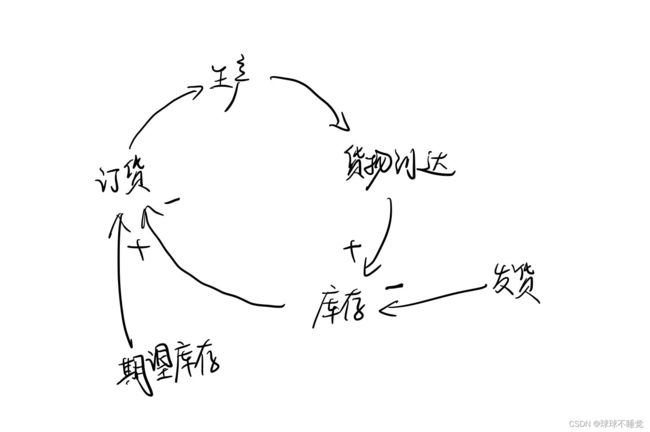
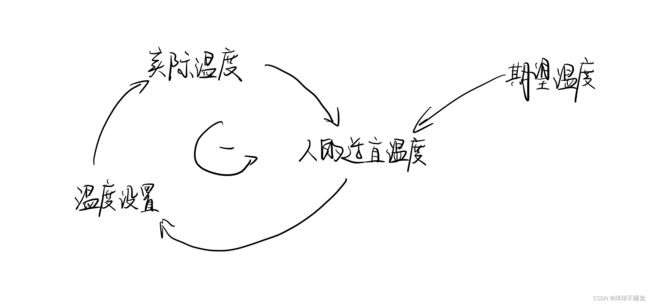
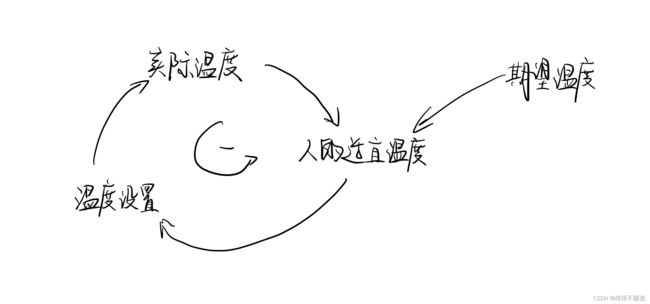
                     例1 恒温系统                                                   例2 库存-订货控制系统

• 1.2.3 反馈的作用与反馈系统的分类

没有反馈的系统（比如开环系统）不能检测到自身的行为，不能对其行为作出反应，也不能作自我调整。

正反馈特点：能产生自身运动的加强过程，在此过程中运动或动作所引起的后果将回授，使原来的趋势得到增强。

负反馈特点：能自动寻求给定的目标，未达到（或未趋近）目标时将不断作出回应。

具有正反馈特性的回路称为正反馈回路，具有负反馈特性的回路称为负反馈回路。分别以两种回路起主导作用的系统则称之为正反馈系统与负反馈系统。

                         例3 正反馈回路                                                      例4 负反馈回路

• 1.3 系统的结构与描述
• 1.3.1 系统的结构

结构包含两层意思，首先指组成系统的各单元，其次指各单元间的作用和关系。

系统动力学认为一阶反馈回路是构成系统的基本结构。

系统结构一般存在以下体系与层次：

（1）确定系统S范围的界限

（2）子系统或子结构Si(i=1,2,...,p)

（3）系统的基本单元，反馈回路结构Ej(j=1,2,...,m)

（4）反馈回路的组成与从属成分：

         反馈回路的主要变量——状态变量和变化率（速率）。

系统界限是指系统范围，规定了形成某特定动态行为所应包含的最小数量的单元。界限内为系统本身，界限外则为环境。

系统的基本结构是一阶反馈回路。对应于系统的三个组成部分是单元、运动和信息。状态变量的变化取决于决策或行动的结果。

决策的产生分为两种：一种是依靠信息反馈的自我调节（生物界、社会经济系统、机器系统），另一种是在一定条件下不依靠信息的反馈，而按照系统本身的某种特殊规律（非生物界）。

一个反馈回路就是由状态、速率、信息三个基本部分组成的基本结构。一个复杂系统则按一定的系统结构由若干个相互作用的反馈回路所组成。

o

                             系统的基本机构之一                                          系统的基本结构之二

• 1.3.2 系统的一般描述

（1）状态

          状态是完整地描述系统的时域行为的最小一组变量。给定t=t0时该组变量的值及t大于等于t0时的输入函数，则系统在t大于等于t0的任何瞬时行为就完全确定了。这样一组变量称为状态变量，组成的向量称为状态向量。

（2）状态空间

          以状态变量为坐标轴所张成的欧氏空间称为状态空间。各瞬刻系统的状态则构成状态空间中的一条轨线。

定常系统或时不变系统是时变系统的特殊情况。

当系统包含依赖于控制或扰动的项，不论是定常的或是非定常的，均称之为强制系统。

当系统的状态方程与输出方程不受控制或扰动的影响时，则此类系统称为自由系统。

• 1.3.3 系统动力学对系统的描述

系统动力学对系统的描述可归纳为如下两步。

（1）首先，根据分解原理把系统S划分为若干个相互关联的子系统Si。各子系统之间的相互关系可通过关系矩阵的非主导元反映出来。在实际问题中系统内的某子系统与其他子系统的直接联系是少量的、有限的，因此关系矩阵是分块对角优势的。

（2）其次，对子系统Si的描述。子系统由基本单元、一阶反馈回路组成，一阶反馈回路包含三种基本的变量：状态变量、速率变量和辅助变量。这三种变量可分别由状态方程、速率方程、辅助方程表示。

复杂系统中，机理尚不清楚，难于用数学描述表示的部分，称为不良结构。不良结构只能半定量、半定性或定性。近年的优化是将不良结构相对地良化，用近似的良结构代替不良结构，或定性与定量结合把一部分定性问题定量化，尚无定量化与半定量化的部分则以定性的方法处理。

• 1.4 系统动力学的基本观点

当系统行为出现指数规律增长趋势时，是因为系统中有起主导作用的一阶正反馈回路。当系统受到干扰偏离原来状态又能自动返回并趋向起始状态时，则表明系统中至少存在一个很强的一阶负反馈回路。系统发生振荡行为则表明系统存在二阶以上的反馈回路或者一个一阶负反馈回路加上一个一阶以上的延时环节。S形增长特性则是一阶正反馈回路与一阶负反馈回路由非线性环节相联结而产生的。

• 1.5 系统动力学分析、研究、解决问题的方法、主要过程与步骤
• 1.5.1 定性与定量结合，系统、分析、综合、推理的方法

系统动力学研究问题的方法是定量与定性相结合，系统、分析、综合与推理的方法。它是定性分析与定量分析的统一，以定性分析为先导，定量分析为支持，两者相辅相成，螺旋上身逐步深化、解决问题的方法。

• 1.5.2 系统动力学解决问题的主要步骤

（1）用系统动力学的理论、原理和方法对被研究的对象进行系统全面的了解、调查分析

（2）进行系统的结构分析，划分系统层次与子块，确定总体与局部的反馈机制

（3）运用软件建立定量、规范的软件

（4）以系统动力学理论为指导，借助模型进行模拟与政策分析，进一步剖析系统得到更多信息，发现新的问题并反过来修改模型。

（5）检验评估模型

• 2 系统动力学构模原理、方法和模型体系的演进
• 2.1 动力学问题

动力学问题包含两个特点：

（1）动态的，包含的量随着时间变化。

（2）包含了反馈概念。

• 2.2 系统的界限

在边界内部凡涉及与所研究的动态问题有重要关系的概念与变量均应考虑进模型。

按照SD的观点，正确地划出系统界限的一条准则是把系统中的反馈回路考虑成闭合的回路。

• 2.3 模型构思
• 2.3.1 构模原则

（1）明确建模的目的。

（2）集中于问题与矛盾，而不是整个系统。

（3）构模的另一条原则是系统动力学仅处理那些随时间而变化和源自反馈结构的问题。

• 2.3.2 动态地定义问题

参考模式：指用图形表示出重要变量，并用推论和绘出与这些最有关的其他重要的量，从而突出、集中地勾画出有待研究的问题的发展趋势与轮廓。可用来鉴定系统模型的有效性。

当没有参考模式时，提出关于变更政策的影响，有经验的构模者往往列举有可能的政策极其影响。

• 2.4 图像表示
• 2.4.1 系统框图

先粗后细，先主后次。

• 2.4.2 因果与相互关系回路图法

因果与相互关系回路图往往用于：

（1）构思模型的初始阶段

（2）非技术性地、直观地描述模型结构，便于与不熟悉系统动力学的人进行交流讨论。

普遍用于构思模型的初始阶段，成熟的构模者可以不做。

因果关系图的重要缺点：在因果关系图中，为了简便，忽略了信息反馈链与物质流的差别。

• 2.4.2.1 定义

图中的个别因果链可标明其影响作用的性质。正号表明，箭头指向的变量将随着箭头源发的变量的增加而增加、减少而减少；而负号表明变量间取与此相反的关系。但正负号并不表示变量间存在比例关系。

• 2.4.2.2 回路极性

确定回路极性的原则：

（1）若反馈回路包含偶数个负的因果链，则极性为正

（2）若反馈回路包含奇数个负的因果链，则极性为负

反馈回路的极性取决于回路中因果链符号的乘积。

• 2.4.3 流图法

速率或称变化率，随着时间的推移，使状态变量的值增或减。

仿真中云状的符号表示源(sources)与漏与沟(sinks)，它们代表输入与输出状态或称位(level)的一切物质。

流图能清楚区分信息流与物质流。信息流用虚线表示，物质流用实线表示。

• 2.4.4 混合图

混合图就是在因果关系图中，把状态和速率变量表示出来。混合图全部用实线表示。

• 2.4.5 图解分析法

图解法简单、形象、清晰，它最可贵的特点在于能够分析解决用一般线性分析解析方法无法解决的简单非线性系统的问题。图解法无法胜任对于复杂系统的分析研究任务。

• 3 Vensim建模基础
• 3.1 概述

变化速率随时间而变化时，计算机处理连续变量就是将它离散化，所以Vensim在模拟时会把连续的时间分割成小的时间间隔，在各小间隔内速率是固定的，然后逐段地加以计算，实际上是一个积分的过程。

• 3.2 变量与方程
• 3.2.1 变量

状态变量：积累变量，是最终决定系统行为的变量，随着时间的变化，当前时刻的值等于过去时刻的值加上这一段时间的变化量。

速率变量：是直接改变积累变量值的变量，反映积累变量输入或输出的速度，本质上和辅助变量没有区别。

辅助变量：辅助变量由系统中其他变量计算获得，当前时刻的值和历史时刻的值是相互独立的。

常量：常量值不随时间变化。

外生变量：随时间变化，但是这种变化不是由系统中其他变量引起的。

• 3.2.2 变量方程

（1）状态变量方程

（2）速率方程

（3）辅助方程

外生变量影响到其他系统内生变量但不受内生变量影响，所以往往是关于时间t的函数。如天气，就需要根据天气预报建立关于t的表函数。

• 3.2.3 表函数（lookup function)

模型中往往需要描述某些变量之间的非线性关系，这很难通过简单的变量之间运算组合来实现，比较方便的是能够以图形方式给出这种非线性关系。

建立表函数的一般步骤是：

（1）确定表函数中的自变量和因变量；

（2）明确变量的取值变化范围，通常通过历史数据和预测数据来确定；

（3）考虑曲线的形状和斜率，在什么范围内曲线是平缓的，什么范围内曲线坡度高，要符合自变量和因变量之间的影响关系，其中正斜率表示正反馈，负斜率表示负反馈；

（4）选取合适的曲线端点、驻点、拐点；

（5）作出图形，通常用x轴表示自变量，y轴表示因变量。

表函数曲线并不是一个光滑的曲线，它也是通过离散化来实现的。

简单例子：十个x对应十个y。建立这些点之间的连线就可以描述这两个变量之间的关系，在vensim中用Graph lookup editor 来实现这一功能。除了已给出的点，可用点之间的斜率求出。当自变量的值溢出表函数中的定义的范围，那么vensim会默认溢出的自变量值对应的因变量输出值为曲线的端点值，同时发出警告信息。解决这样的问题可以通过扩大取值范围来实现。

• 3.3 延迟、平滑和平滑函数
• 3.3.1 物质延迟

（1）DELAY1I：一阶延迟

DELAY1I形式为：DELAY1I(input,delay time,initial value)

DELAY1I=LV(t)/DT

LV(t)=LV(t0)+

LV(t0)=IVxDT

IV表示initial value，DT表示delay time.

以DELAY1I替代一组方程，使用方便，缺点是状态变量被隐含，不输出它的结果。

（2）DELAY3I：三阶延迟

（3）DELAY FIXED

• 3.3.2 物质延迟的阶次

一阶与三阶曲线差别很大，增长模式全然不同，但三阶曲线与六阶甚至十二阶曲线比无本质区别，只是程度上差异而已，同样是S形模式。Vensim中备有一阶函数和三阶函数，而无更高阶次的单个函数。若建模者认为确实有必要应用高于三阶的延迟函数，可以用两个三阶函数串成六阶函数。

• 3.3.3 平滑函数

SVAR(t)=SMOOTH[VAR(t),STIME]

其中，SVAR为平滑变量，VAR为待平滑变量，STIME为平滑时间。

• 3.3.4 信息延迟

类似于物质延迟。

• 3.4 函数
• 3.4.1 数学函数
• 3.4.2 逻辑函数

MAX, MIN, IF ELSE THEN

• 3.4.3 测试函数

（1）阶跃函数

（2）斜坡函数

（3）脉冲函数

（4）正弦函数

（5）正态分布函数

• 3.5 输出问题

动力学模拟软件可以提供的输出：

（1）时间序列的数据输出。

（2）时间序列的图形输出。

（3）变量之间的关系图。

（4）因果关系分析，以及反馈分析等静态分析的输出。

• 3.6 准确度与运行时间单位的选择

选择time step的经验法则是，取其值为（0.1~0.5）倍的模型最小时间常数，取小于0.5倍可防止出现不合理的计算结果，但若取小于0.1倍则对于计算的准确度提高不大，且耗费大量的计算机时。

如计算最小时间常数为1/CONST=1/0.2=5，time step=(0.1~0.5)*5=0.5~0.25（分）。

• 4 一阶系统
• 4.1 一阶系统的数学描述

一阶微分方程式等式右侧保留一项，为指数增长规律或自然增长规律。

一阶微分方程式等式右侧保留两项，曲线呈S形增长特性，通常称为Sigmoid或logistic曲线。

• 4.2 一阶系统的重要参数
• 4.2.1 指数增长及其参数

（1）指数增长方程式

其中，LEV(t)为状态在t时的值，LEV(0)为状态的初始值，CONST为比例常数。

（2）时间常数T

T=1/CONST,具有时间的量纲。

LEV(T)=2.73LEV(0),LEV(2T)=7.45LEV(0)

（3）倍增时间(doubling time)Td

倍增时间定义为变量由初始值倍增至二倍的初始值所需的时间。

推导可知，Td=0.69T，倍增时间约等于70%的时间常数T。

• 4.2.2 一阶负反馈系统的重要参数

（1）方程式的基本形式

其中，LEV(t)为状态在t时的值；LEV(0)为初始状态值；GL为目标值；CONST为比例常数。

（2）时间常数T

 

表明在时间t内，状态值与其目标值接近的程度。

表明在时间t内，状态值与目标值之差距。

经过3倍的时间常数T之后状态值接近目标值的程度已达大约95%，而经过4T后则约达99%。

（3）减半时间函数（或半衰期）（halving time)Th与时间常数T的关系

如果负反馈是指数衰减过程，状态值减半所需时间

减半时间Th约等于0.69倍的系统时间常数T。

• 4.3 正反馈系统
• 4.3.1 正反馈的一般结构

流图中的状态变量LEV为单向流的物质积累。任何有关状态数量上变动的信息，经速率RT控制进入LEV的流量。假定RT正比于LEV，RT等于LEV乘以常数CONST。若CONST=0.2，LEV的初始值为1，则系统的方程如下：

其中，DT为计算时间间隔（年）；CONST为常数（1/年）；LEV为状态变量（单位）；RT为速率（单位/年）。

• 4.3.2 正反馈系统特征

（1）在相当长的时间内增长极慢，然后突然爆炸性地增长上去。

（2）超指数增长。

• 4.4 负反馈结构
• 4.4.1 负反馈结构基本方程式

负反馈结构基本方程式：

其中，LEV为状态单位；RT为速率（单位/时间）；CONST为常数（1/时间）；DISC为偏差（单位）；GL为目标值（单位）。

• 4.4.2 系统特性

LEV随时间变化的曲线包括两个区段：瞬态和稳态。在瞬态区段中，LEV值与目标值GL不相等。此时LEV具有寻的与瞬变的特点。在稳态区则是接近或近似地达到目标值，稳定不变。RT也最终近似地达到0值。

• 4.5 负反馈系统的补偿特性

负反馈系统具有力图维持系统处于平衡状态的特性。在最简单的系统中，基于状态值与目标值之差的速率发挥调节作用，驱动系统状态趋向目标值。而时间常数决定系统对状态变化的反应速度。

4.6 S形增长的反馈结构

S形增长包含了指数与渐进两种增长过程。稳态区前的过渡区是由两种明显不同的增长过程组成，先是指数增长，继之渐近增长。前者是正反馈起主导作用，后者是由负反馈起主导作用。