算法及时间、空间复杂度

算法

算法是对问题求解过程的一种描述，是为解决一个或一类问题给出的一个确定的、有限长的操作序列。严格说来，一个算法必须满足以下5个重要特性：
（1）有穷性：对于任意一组合法的输入值，在执行有穷步骤之后一定能结束，即算法中的操作步骤为有限个，且每个步骤都能在有限时间内完成。
（2）确定性：对于每种情况下所应执行的操作，在算法中都有确切的规定，使算法的执行者和阅读者都能明确其含义及如何执行。并且在任何条件下，算法都只有一条执行路径。
（3）可行性：算法中的所有操作都必须足够基本，都可以通过已经实现的基本操作运算有限次实现。
（4）有输入：作为算法加工对象的量值，通常体现为算法中的一组变量。有些输入量需要在算法执行过程中输入，而有的算法表面上可以没有输入，实际上输入已被嵌入算法之中。
（5）有输出：它是一组与“输入”有确定关系的量值，是算法进行信息加工后得到的结果，这种确定关系即为算法的功能。

时间复杂度

算法的效率指的是算法的执行时间随问题规模的增长而增长的趋势。假如随着问题规模n的增长，算法执行时间的增长率和f(n)的增长率相同，则可记作：

T(n)=O(f(n))

称T(n)为算法的(渐近)时间复杂度。
T(n)表示代码执行的时间; n表示数据规模的大小; f(n) 表示每行代码执行的次数总和。因为这是一个公式，所以可以用f(n)来表示。公式中的O,表示的是代码的执行时间T(n)与f(n)表达式成正比。

当n很大时，你可以把它想象成999999、9999999999。 而公式中的低阶、常量、系数三部分并不左右增长趋势,所以都可以忽略。我们只需要记录一个最大量级就可以了。

比如：
T(n)=O(5n+5)，将它的系数和常量忽略，就可以看成是T(n)=O(n);
T(n)=O(5n²+5n+5)，将它的低阶、常量、系数三部分忽略后，就可以看成是T(n)=O(n²)。

复杂度分析法则：
（1）单段代码看高频：比如循环。
（2）多段代码取最大：比如一段代码中有单循环和多重循环，那么取多重循环的复杂度。
（3）嵌套代码求乘积：比如递归、多重循环等
（4）多个规模求加法：比如方法有两个参数控制两个循环的次数，那么这时就取二者复杂度相加。

时间复杂度分析：
只关注循环执行次数最多的一段代码
加法法则：总复杂度等于量级最大的那段代码的复杂度
乘法法则：嵌套代码的复杂度等于嵌套内外代码复杂度的乘积

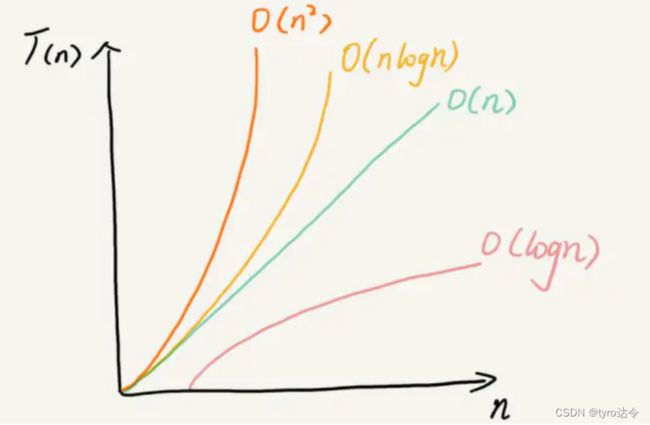
几种常见的时间复杂度：

如果一段代码的时间复杂度是O(logn) ，我们循环执行 n 遍，时间复杂度就是 O(nlogn) 。
多项式阶：随着数据规模的增长，算法的执行时间和空间占用，按照多项式的比例增长。包括，O(1)（常数阶）、O(logn)（对数阶）、O(n)（线性阶）、O(nlogn)（线性对数阶）、O(n²)（平方阶）、O(n³)（立方阶）
非多项式阶：随着数据规模的增长，算法的执行时间和空间占用暴增，这类算法性能极差。包括，O(2ⁿ)（指数阶）、O(n!)（阶乘阶）

求下列程序段的时间复杂度：

i=1;
while(i<=n) 
{
   i = i*3;
}

假设循环执行次数是k，则i=3^k-1。转化一下，有3^k-1<=n，解之得到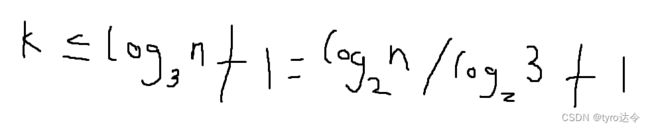
所以时间复杂度是O(logn)。

空间复杂度

算法的存储量指的是算法执行过程中所需的最大存储空间。算法执行期间所需要的存储量应该包括以下三部分：
(1)输入数据所占空间
(2)程序本身所占空间
(3)辅助变量所占空间

类似于算法的时间复杂度，通常以算法的空间复杂度作为算法所需存储空间的量度。定义算法空间复杂度为

S(n)=O(g(n))

表示随着问题规模n的增大，算法运行所需存储量的增长率与g(n)的增长率相同。

常见的空间复杂度就是O(1)、O(n)、O(n²)，像O(logn)、O(nlogn)这样的对数阶复杂度平时都用不到。

举例：

void print(int n) 
{
    int i=0;
    int[]a=new int[n];
    for (i;i<n;++i) 
    {
        a[i]=i*i;
    }
    for(i=n-1;i>=0;--i)
    {
        print out a[i]
    }
}

我们可以看到，第三行代码中，我们申请了一个空间存储变量i,但是它是常数阶的，跟数据规模n没有关系，所以我们可以忽略。第四行申请了一个大小为n的int类型数组，除此之外，剩下的代码都没有占用更多的空间，所以整段代码的空间复杂度就是O(n)。

复杂度分析的4个概念：
1.最坏情况时间复杂度：代码在最坏情况下执行的时间复杂度。
2.最好情况时间复杂度：代码在最理想情况下执行的时间复杂度。
3.平均时间复杂度：代码在所有情况下执行的次数的加权平均值。
4.均摊时间复杂度：在代码执行的所有复杂度情况中绝大部分是低级别的复杂度，个别情况是高级别复杂度且发生具有时序关系时，可以将个别高级别复杂度均摊到低级别复杂度上。基本上均摊结果就等于低级别复杂度。

三、如何分析平均、均摊时间复杂度？
1.平均时间复杂度
代码在不同情况下复杂度出现量级差别，则用代码所有可能情况下执行次数的加权平均值表示。
2.均摊时间复杂度
两个条件满足时使用：（1）代码在绝大多数情况下是低级别复杂度，只有极少数情况是高级别复杂度；（2）低级别和高级别复杂度出现具有时序规律。均摊结果一般都等于低级别复杂度。