机器学习笔记之概率图模型(四)基于贝叶斯网络的模型概述
机器学习笔记之概率图模型——基于贝叶斯网络的模型概述
- 引言
-
- 基于贝叶斯网络的模型
-
- 场景构建
- 朴素贝叶斯分类器
- 混合模型
- 基于时间变化的模型
- 特征是连续型随机变量的贝叶斯网络
- 动态概率图模型
- 总结
引言
上一节介绍了判别变量/特征之间是否具备条件独立性的方法—— D \mathcal D D划分,本节从贝叶斯网络整体出发,总结 贝叶斯网络家族 中包含哪些 模型(Representation)。
基于贝叶斯网络的模型
场景构建
数据集合 X \mathcal X X依然是包含 N N N个样本,并且每个样本均包含 p p p个维度的特征信息:
这里的样本特征是‘离散型随机变量’~
X = ( x 1 , x 2 , ⋯ , x p ) T = ( x 1 ( 1 ) , x 2 ( 1 ) , ⋯ , x p ( 1 ) x 1 ( 2 ) , x 2 ( 2 ) , ⋯ , x p ( 2 ) ⋮ x 1 ( N ) , x 2 ( N ) , ⋯ , x p ( N ) ) N × p x ( i ) ∈ R p ; i = 1 , 2 , ⋯ , N \mathcal X = \left(x_1,x_2,\cdots,x_p\right)^T = \begin{pmatrix} x_1^{(1)},x_2^{(1)},\cdots,x_p^{(1)} \\ x_1^{(2)},x_2^{(2)},\cdots,x_p^{(2)} \\ \vdots \\ x_1^{(N)},x_2^{(N)},\cdots,x_p^{(N)} \\ \end{pmatrix}_{N \times p} x^{(i)} \in \mathbb R^p;i=1,2,\cdots,N X=(x1,x2,⋯,xp)T=⎝ ⎛x1(1),x2(1),⋯,xp(1)x1(2),x2(2),⋯,xp(2)⋮x1(N),x2(N),⋯,xp(N)⎠ ⎞N×px(i)∈Rp;i=1,2,⋯,N
如果是监督学习,数据集合 X \mathcal X X对应的标签集合 Y \mathcal Y Y是一个 N × 1 N \times1 N×1的向量形式。而每个样本 x ( i ) ∈ X x^{(i)} \in \mathcal X x(i)∈X对应的标签结果 y ( i ) ∈ Y y^{(i)} \in \mathcal Y y(i)∈Y是一个 标量:
Y = ( y ( 1 ) , y ( 2 ) , ⋯ , y ( N ) ) T \mathcal Y = \left(y^{(1)},y^{(2)},\cdots,y^{(N)}\right)^T Y=(y(1),y(2),⋯,y(N))T
朴素贝叶斯分类器
从假设的角度观察,关于样本特征之间最简单的假设即朴素贝叶斯假设:在分类结果给定的条件下(假设共包含 k k k个分类),各分类下的样本集合 X l ( l = 1 , 2 , ⋯ , k ) \mathcal X_l(l = 1,2,\cdots,k) Xl(l=1,2,⋯,k)中的任意两个不同特征之间相互独立。数学符号表示如下:
x i ⊥ i j ∣ Y = l { i , j ∈ { 1 , 2 , ⋯ , p } ; i ≠ j ; l ∈ { 1 , 2 , ⋯ , k } ; x_i \perp i_j \mid \mathcal Y = l \quad \begin{cases} i,j \in \{1,2,\cdots, p\};\\ i \neq j;\\ l \in \{1,2,\cdots,k\};\end{cases} xi⊥ij∣Y=l⎩ ⎨ ⎧i,j∈{1,2,⋯,p};i=j;l∈{1,2,⋯,k};
对应的概率图模型是朴素贝叶斯分类器。其贝叶斯网络表示如下:
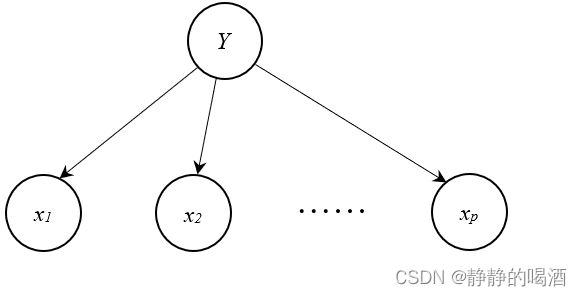
基于朴素贝叶斯假设的 概率分布 P ( X ∣ Y ) \mathcal P(\mathcal X \mid \mathcal Y) P(X∣Y)表示如下:
P ( X ∣ Y = l ) = P ( x 1 , ⋯ , x p ∣ Y = l ) = ∏ i = 1 p P ( x i ∣ Y = l ) l ∈ { 1 , 2 , ⋯ , k } \begin{aligned} \mathcal P(\mathcal X \mid \mathcal Y = l) & = \mathcal P(x_1,\cdots,x_p \mid \mathcal Y = l) \\ & = \prod_{i=1}^p \mathcal P(x_i \mid \mathcal Y = l) \quad l \in \{1,2,\cdots,k\} \end{aligned} P(X∣Y=l)=P(x1,⋯,xp∣Y=l)=i=1∏pP(xi∣Y=l)l∈{1,2,⋯,k}
从贝叶斯网络的角度观察朴素贝叶斯分类器的概率图模型:
- 上述贝叶斯网络中一共包含 p p p条有向边;
- 任意两条有向边都能组成同父结构(Common Parent);传送门
- 在 Y \mathcal Y Y给定的条件下,任意两个特征之间均条件独立。
混合模型
观察朴素贝叶斯假设,它的假设方式是单一的:给定标签特征 Y \mathcal Y Y的条件下,就已经将各样本特征 ( x 1 , x 2 , ⋯ , x p ) (x_1,x_2,\cdots,x_p) (x1,x2,⋯,xp)相互独立地划分开来:
x 1 ⊥ x 2 ⊥ ⋯ ⊥ x p ∣ Y x_1 \perp x_2 \perp \cdots \perp x_p \mid \mathcal Y x1⊥x2⊥⋯⊥xp∣Y
可能存在如下情况:单独观察各维度样本特征,可能无法观测到其独立性的表现;如果将各维度样本特征融合 → \to → 从样本的角度能够明显地观察其独立关系。
称这种模型为混合模型。其中混合模型最具代表性的是用作聚类任务的高斯混合模型(Gaussian Mixture Model,GMM)。其贝叶斯网络表示如下:

其中 Z \mathcal Z Z表示隐变量,是一个离散型随机变量:
其每个取值均对应一个分类;
Z ∈ { 1 , 2 , ⋯ k } \mathcal Z \in \{1,2,\cdots k\} Z∈{1,2,⋯k}
而数据集合 X \mathcal X X是 给定 Z \mathcal Z Z取值的条件下,从概率模型 P ( X ∣ Z ) \mathcal P(\mathcal X \mid \mathcal Z) P(X∣Z)中生成的样本:
X ∣ Z = l ∼ N ( μ l , Σ l ) l ∈ { 1 , 2 , ⋯ , k } \mathcal X \mid \mathcal Z= l \sim \mathcal N(\mu_l,\Sigma_l) \quad l \in \{1,2,\cdots,k\} X∣Z=l∼N(μl,Σl)l∈{1,2,⋯,k}
从贝叶斯网络角度观察,貌似该网络并不满足前面介绍的三种结构,为了更直观的表达高斯混合模型的假设,将上述贝叶斯网络修改为如下形式:

可以发现,隐变量 Z \mathcal Z Z各标签下的融合特征之间在给定 Z \mathcal Z Z条件下,属于同父结构。即 各标签条件下的各融合特征 ( x 1 , ⋯ , x p ) (x_1,\cdots,x_p) (x1,⋯,xp)之间均条件独立。
基于时间变化的模型
如果从时间或者序列角度观察,增加特征在时间上的变化信息,即:样本特征随着时间的变化发生变化。最具代表性的模型是马尔可夫链(MCMC方法中有介绍)(Markov Chain)。其贝叶斯网络表示如下:

其中结点中的 X i ( i = 1 , 2 , ⋯ , T ) \mathcal X_i(i=1,2,\cdots,T) Xi(i=1,2,⋯,T)表示如下:
X i = ( x 1 , x 2 , ⋯ , x p ) ∣ t = i i ∈ { 1 , 2 , ⋯ , T } \mathcal X_i = (x_1,x_2,\cdots,x_p)\mid_{t=i} \quad i \in \{1,2,\cdots,T\} Xi=(x1,x2,⋯,xp)∣t=ii∈{1,2,⋯,T}
而马尔可夫链满足马尔可夫性质。以一阶齐次马尔可夫假设为例,马尔可夫性质表示如下:
X i + 1 ⊥ X j ∣ X i s . t . { i , j ∈ { 1 , 2 , ⋯ , T } j < i \mathcal X_{i+1} \perp \mathcal X_{j} \mid \mathcal X_i \quad s.t. \begin{cases} i,j \in \{1,2,\cdots,T\} \\ j < i \end{cases} Xi+1⊥Xj∣Xis.t.{i,j∈{1,2,⋯,T}j<i
从贝叶斯网络的角度观察马尔可夫链,我们发现:任意三个连续结点之间均属于顺序结构。即:
X i − 1 ⊥ X i + 1 ∣ X i \mathcal X_{i-1} \perp \mathcal X_{i+1} \mid \mathcal X_i Xi−1⊥Xi+1∣Xi
于此同时,如果增加连续结点,如 X i − 2 , X i − 3 , ⋯ \mathcal X_{i-2},\mathcal X_{i-3},\cdots Xi−2,Xi−3,⋯,只要 X i \mathcal X_i Xi给定的条件下, X i − 1 , X i − 2 , X i − 3 , ⋯ \mathcal X_{i-1},\mathcal X_{i-2},\mathcal X_{i-3},\cdots Xi−1,Xi−2,Xi−3,⋯均和 X i + 1 \mathcal X_{i+1} Xi+1条件独立。这完全和齐次马尔可夫假设相吻合。
特征是连续型随机变量的贝叶斯网络
上面介绍的模型,它们的共同点是:随机变量 X \mathcal X X的特征均是离散型随机变量。具有代表性的是高斯网络(Gaussian Network)。而特征的连续性在有向图和无向图中均可以表示,我们将 特征连续性服从高斯分布的贝叶斯网络 称为高斯贝叶斯网络(Gaussian Bayessian Network,GBN)。
动态概率图模型
在概率模型背景的阶段性介绍中提到过,动态概率图模型是在 混合模型的基础上,增加变量在时间上的变化信息。即:隐变量 Z \mathcal Z Z随着时间的变化而变化,通过影响 Z \mathcal Z Z的变化,从而影响特征 X \mathcal X X的变化。
注意这里的描述,这里说的‘变量’不一定是指样本特征(观测变量),还有可能是‘隐变量’。这和‘马尔可夫链’的描述存在一些差异。
这里可以将动态概率模型看作是混合模型与基于时间变化模型的结合体。动态概率图模型中最具代表性的是隐马尔可夫模型。
隐马尔可夫模型的贝叶斯网络表示如下:
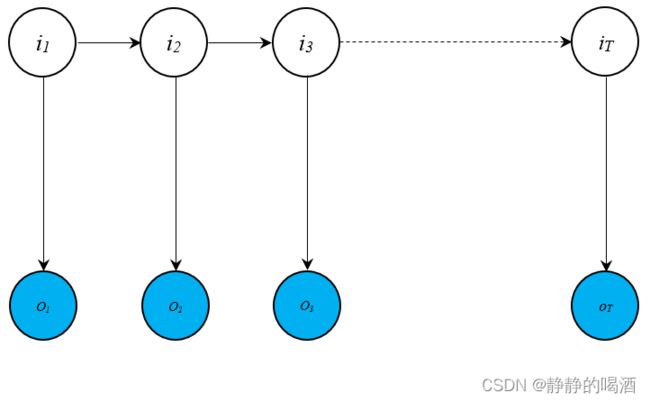
其中,模型中隐状态序列是一条马尔可夫链,并且隐状态 Z \mathcal Z Z中的各特征是离散型随机变量。
我们同样可以根据贝叶斯网络观察隐马尔可夫模型中的两条假设:
- 齐次马尔可夫假设。
该假设与上述‘马尔可夫链’中的假设描述完全相同,这里不多赘述。 - 观测独立性假设。即:某时刻观测变量 o t o_t ot的条件概率,只和当前时刻的状态变量 i t i_t it相关,与其他变量无关。数学符号表示如下:
P ( o t ∣ i t , i t − 1 , ⋯ , i 1 , o t − 1 , ⋯ , o 1 ) = P ( o t ∣ i t ) \mathcal P(o_t \mid i_t,i_{t-1},\cdots,i_1,o_{t-1},\cdots,o_1) = \mathcal P(o_t \mid i_t) P(ot∣it,it−1,⋯,i1,ot−1,⋯,o1)=P(ot∣it)
我们从上述贝叶斯网络中观察:
以 o 2 o_2 o2为例。与 o 2 o_2 o2相关联的结点子图 表示如下:
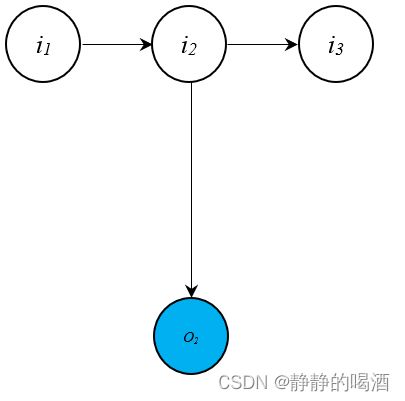
观察上述子图:
- i 1 , i 2 , o 2 i_1,i_2,o_2 i1,i2,o2三个结点之间构成顺序结构,在给定 i 2 i_2 i2的条件下, o 2 o_2 o2与 i 1 i_1 i1条件独立:
o 2 ⊥ i 1 ∣ i 2 o_2 \perp i_1 \mid i_2 o2⊥i1∣i2 - o 2 , i 2 , i 3 o_2,i_2,i_3 o2,i2,i3三个结点之间构成同父结构,在给定 i 2 i_2 i2的条件下, o 2 o_2 o2与 i 3 i_3 i3条件独立:
o 2 ⊥ i 3 ∣ i 2 o_2 \perp i_3 \mid i_2 o2⊥i3∣i2
同理,除去 o 2 , i 2 o_2,i_2 o2,i2的其他任意结点与 i 2 , o 2 i_2,o_2 i2,o2构建路径时, i 2 i_2 i2给定的条件下, o 2 o_2 o2与其他结点均条件独立。
总结
本节主要是从贝叶斯网络的图结构角度 认识相关的概率图模型。
基于贝叶斯网络的模型有如下总结:
- 从 单个特征的条件独立性到混合特征的条件独立性;
如高斯混合模型中的样本特征 ( x 1 , ⋯ , x p ) (x_1,\cdots,x_p) (x1,⋯,xp)只和 对应分类的隐变量标签相关联,与其他隐变量结果的结点条件独立:
( x 1 , ⋯ , x p ) ∣ Z = l ⊥ ( x 1 , ⋯ , x p ) ∣ Z = j l , j ∈ { 1 , 2 , ⋯ , k } ; l ≠ j (x_1,\cdots,x_p) \mid \mathcal Z = l \perp (x_1,\cdots,x_p) \mid \mathcal Z = j \quad l,j \in \{1,2,\cdots,k\};l \neq j (x1,⋯,xp)∣Z=l⊥(x1,⋯,xp)∣Z=jl,j∈{1,2,⋯,k};l=j - 从特征变量的离散到连续;
这里指朴素贝叶斯、混合模型等与高斯贝叶斯网络之间的区别。
‘高斯网络’在后续笔记中进行介绍。 - 从模型的静态到动态;
这里指混合模型(静态概率图模型)与动态概率图模型之间的区别。
这里忽略了一些细节。动态概率图模型中,隐马尔可夫模型(HMM)是最具有代表性的模型,其他模型如‘线性动态系统(Kalman Filter)、粒子滤波(Particle Filter)’,它们都属于‘动态模型’。并且它们与HMM共用同一个‘贝叶斯网络’。在后续笔记中进行介绍。
下一节将介绍马尔可夫随机场(Markov Random Field,MRF)。
相关参考:
机器学习-概率图模型4-贝叶斯网络-Representation-具体模型例子