李宏毅深度学习--《Network Compression》
Network Compression
- Network Pruning
- Practical Issue
- Knowledge Distillation
- Parameter Quantization
- Binary Weights
- Architecture Design
-
- Low rank approximation
- Depthwise Separable Convolution
- Dynamic Computation
D e e p n e u r a l n e t w o r k Deep\ neural\ network Deep neural network通常有很多的参数,这会占用大量的内存。而对于一些设备来说,内存空间、运算能力是十分有限的。
若想将 D e e p n e u r a l n e t w o r k Deep\ neural\ network Deep neural network在这些设备上运行,神经网络的压缩是一个可行的解决办法。
下面介绍 5 5 5种 N e t w o r k C o m p r e s s i o n Network\ Compression Network Compression:
- N e t w o r k P r u n i n g ( 网络修剪 ) Network\ Pruning(网络修剪) Network Pruning(网络修剪)
- K n o w l e d g e D i s t i l l a t i o n ( 知识蒸馏 ) Knowledge\ Distillation(知识蒸馏) Knowledge Distillation(知识蒸馏)
- P a r a m e t e r Q u a n t i z a t i o n ( 参数量化 ) Parameter\ Quantization(参数量化) Parameter Quantization(参数量化)
- A r c h i t e c t u r e D e s i g n ( 结构设计 ) Architecture\ Design(结构设计) Architecture Design(结构设计)
- D y n a m i c C o m p u t a t i o n ( 动态运算 ) Dynamic\ Computation(动态运算) Dynamic Computation(动态运算)
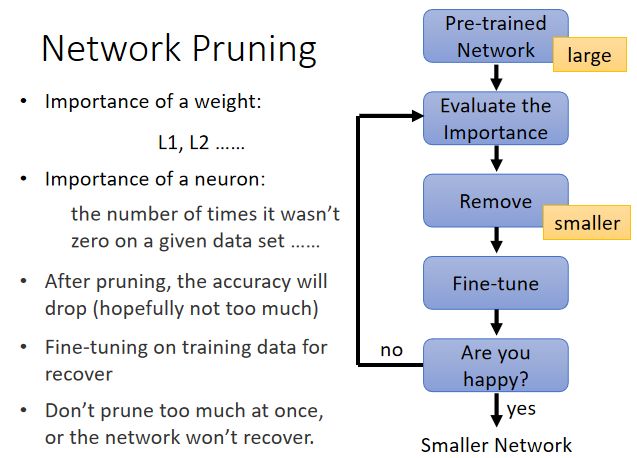
Network Pruning
网络通常过度参数化(存在大量冗余权重或神经元),如有的参数的值为 0 0 0或者是接近 0 0 0的数,对输出 o u t p u t output output没有贡献或者不会影响 o u t p u t output output的结果;对于这些权重或者神经元可以修剪掉。
N e t w o r k P r u n i n g Network\ Pruning Network Pruning流程:
- 对一个 P r e _ t r a i n e d N e t w o r k Pre\_trained\ Network Pre_trained Network进行修剪
- 对神经元/权重的重要性进行评估
- 对于权重的重要性评估,可以通过权重值来判断,越接近 0 0 0其重要性就越低;
- 对于神经结点的重要性评估,可以通过查看该神经结点在数据集的计算过程种输出为 0 0 0的次数作为重要性评判,若 0 0 0出现的次数过多,则该结点对数据的预测影响不大。
- 去掉不重要的神经元/权重
- F i n e − t u n e Fine-tune Fine−tune(微调)
- 修剪后,精度会下降,但希望不会降的太多。所以在修剪后可以进行一次参数的更新;微调是为了恢复因修剪而造成的预测精度丢失。
- 判断修剪后的 S m a l l e r N e t w o r k Smaller\ Network Smaller Network是否满足要求。不满足要求则回到第 2 2 2步;
W h y P r u n i n g ? Why\ Pruning? Why Pruning?
有一个疑问是:为什么不直接在小的网络上直接训练呢?而是先训练大网络再进行修剪。
原因一:
大网络通常会比小网络更容易训练。因为网络模型越大,解空间就会越大,就会更容易找到一个合适的局部最优解。而小网络较难训练,有时甚至无法收敛。
原因一的另一个观察角度:
- 小的网络解空间较小,和最优解的距离就会存在一段距离,因此在训练过程中很难找到合适的局部最优解。
- 对于大网络的训练,在找到局部最优解后,剪枝可能只是去掉了没有意义的解空间,跟最优解的距离不变。
原因二: L o t t e r y T i c k e t H y p o t h e s i s Lottery\ Ticket\ Hypothesis Lottery Ticket Hypothesis
L o t t e r y T i c k e t H y p o t h e s i s Lottery\ Ticket\ Hypothesis Lottery Ticket Hypothesis(大乐透假设)做了以下实验:
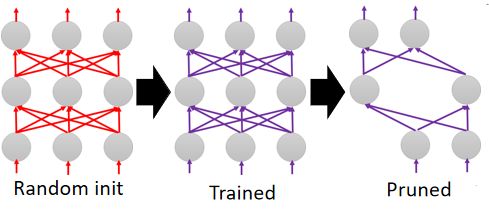
先随机初始化一个大网络 A A A,然后对大网络 A A A进行训练,训练后对 A A A进行修剪得到一个子网络 B B B;如下图:
- 红色箭头:随机初始化的参数
- 紫色箭头:训练后的权重
- 绿色箭头:另一个随机初始化参数(与红色箭头的参数不一样)
接下来对子网络 B B B进行初始化(红色箭头的初始化),即大网络 A A A的初始权重赋值到小网络 B B B上,再对 B B B进行训练, B B B会得到一个很好的训练结果。
而对子网络 B B B采用与大网络 A A A初始参数不同的另一组随机初始化参数,会发现子网络 B B B很难训练得到一个较好的结果。
所以猜测:对于网络模型的训练与初始值有关,就像买乐透一样。当你的参数越多,即买的越多,中将的几率就会越大。
个人理解:
参数越多,解空间越大,那中奖(找到合适解)的概率就会越大。
而小网络参数较少,解空间种的合适解有限,所以小概率中奖,难以训练收敛到局部最优。
然而在论文 R e t h i n k i n g t h e V a l u e o f N e t w o r k P r u n i n g Rethinking\ the\ Value\ of Network\ Pruning Rethinking the Value ofNetwork Pruning中,得出了与大乐透相矛盾的结论:
- 对大网络 A A A通过修剪得到了压缩网络 B B B后,相比使用来自大网络 A A A的初始权重(红色箭头)对压缩网络 B B B进行训练,直接随机初始化训练压缩网络 B B B可以得到更好的训练结果(需要更多的 e p o c h epoch epoch)。
- 所以剪枝算法可以被视为执行网络架构搜索
Practical Issue
在实际应用中,若我们采用 W e i g h t p r u n i n g Weight\ pruning Weight pruning会得到不规则的神经网络结构,如下图:
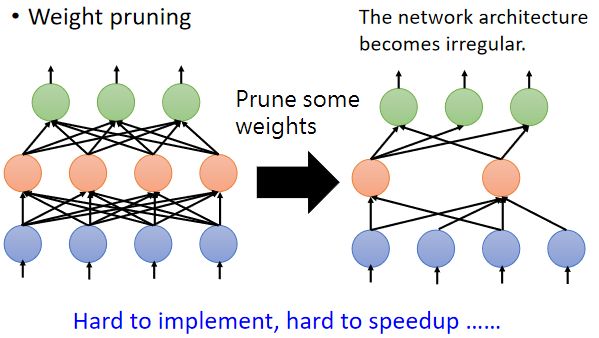
不规则的神经网络结构意味着难以实施,并且难以向量化,从而 G P U GPU GPU难以对其进行加速。
在实验中,我们可以将修剪掉的权重 w e i g h t weight weight设置为 0 0 0,这样可以确保能够进行向量化,可以使用 G P U GPU GPU加速。但是这样只是将 w e i g h t weight weight置0,并没有真正的修剪掉。
因为weight pruning的难以实施,所以通常采用的都是neuron pruning,便于实施且可以GPU加速。如下图:

Knowledge Distillation
知识蒸馏是指:
首先训练一个大网络 ( T e a c h e r N e t ) (Teacher\ Net) (Teacher Net),再用小网络 ( S t u d e n t N e t ) (Student\ Net) (Student Net)学习大网络。
即先使用大网络数据集进行打标签,然后使用这些标签对小网络进行训练;如下图:
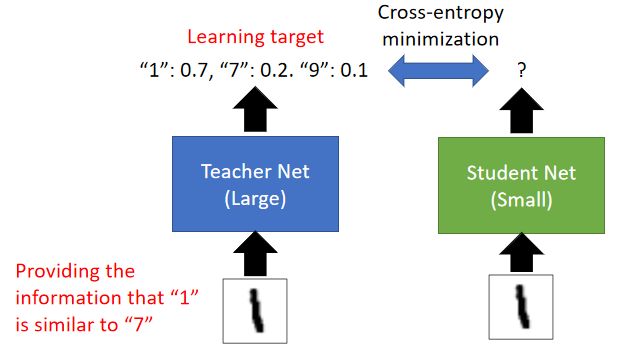
这样的好处在于:小网络可能会学大一些额外的知识。如对大网络输入一张 1 1 1的照片,大网络输出:"1"的概率是0.7,“7”的概率是0.2;小网络从这个概率中会学到 7 7 7和 1 1 1的概率是相对较接近的,所以 7 7 7和 1 1 1的图片是比较相似的。
该方法在实践中神奇之处是,对于某个模型在 t r a i n train train的时候没看过 7 7 7,但在预测的时候还是能得到正确的预测结果
大网络 ( T e a c h e r N e t ) (Teacher\ Net) (Teacher Net)可以是 E n s e m b l e Ensemble Ensemble的,这样小网络 ( S t u d e n t N e t ) (Student\ Net) (Student Net)可以凭借着简单的网络结构来学习到复杂的关系。如下图:
在多分类任务中,大网络 ( T e a c h e r N e t ) (Teacher\ Net) (Teacher Net)的最后一层会通过一个 s o f t m a x softmax softmax层, s o f t m a x softmax softmax函数如下:
y i = e x p ( x i ) ∑ j e x p ( x j ) y_i=\frac{exp(x_i)}{\sum_jexp(x_j)} yi=∑jexp(xj)exp(xi)
当 x 1 = 100 、 x 2 = 10 、 x 3 = 1 x_1=100、x_2=10、x_3=1 x1=100、x2=10、x3=1时,通过 s o f t m a x softmax softmax函数后,得到的值 y 1 ≈ 1 、 y 2 ≈ 0 、 y 2 ≈ 0 y_1≈1、y_2≈0、y_2≈0 y1≈1、y2≈0、y2≈0,此时标签集和 r e a l l a b e l real\ label real label一样了。对于小网络来说就很难学到额外的信息了。
对此可以添加一个参数 T T T,将 s o f t m a x softmax softmax函数改成:
y i = e x p ( x i / T ) ∑ j e x p ( x j / T ) y_i=\frac{exp(x_i/T)}{\sum_jexp(x_j/T)} yi=∑jexp(xj/T)exp(xi/T)
对于上述的 x x x,可以得到 y 1 ≈ 0.56 、 y 2 ≈ 0.23 、 y 2 ≈ 0.21 y_1≈0.56、y_2≈0.23、y_2≈0.21 y1≈0.56、y2≈0.23、y2≈0.21。此时小网络可以学到 y 1 y_1 y1可能和 y 2 、 y 3 y_2、y_3 y2、y3相差较大, y 2 、 y 3 y_2、y_3 y2、y3是比较类似的。
【但老师说该方法在实际运用中用处不大】
Parameter Quantization
该方法可总结为两句话:
- Weight clustering (权重聚类)
- Using less bits to represent a value(使用更少的编码表示权重)
如下图,有一个 4 × 4 4\times 4 4×4的权重矩阵,先对权重进行聚类(可以使用 K N N KNN KNN之类的聚类),图中是分成了 4 4 4类;然后使用2个bits的编码来分别表示这 4 4 4类,最后在通过一个表格映射从权重类别到权重值(即用一个值来近似一类权重的值)。表格中的权重值可以是该类权重值得平均。
可以使用 H u m f f m a n e n c o d i n g Humffman\ encoding Humffman encoding来优化上述过程。
Binary Weights
第二种参数量化方式是Binary Weights,即权重总是 − 1 -1 −1或者 1 1 1,这样参数只用一个单位就能表示了。
下面介绍一篇论文 B i n a r y C o n n e c t Binary\ Connect Binary Connect中的思路:
下图中的灰色点代表一组全为 − 1 、 1 -1、1 −1、1的参数,蓝色的点代表当前训练网络中的真实参数(即参数不一定是 − 1 、 1 -1、1 −1、1)。

首先算出最接近蓝色点的灰色结点,然后计算灰色结点的梯度方向(下图的红色箭头)。

随后将蓝色点参数向红色箭头方向进行梯度下降(参数更新),此时蓝色点走到了一个新的位置。如下图:

经过多轮迭代后,将距离蓝色点最近的灰色点(下图红色圈出的点)作为模型的参数:

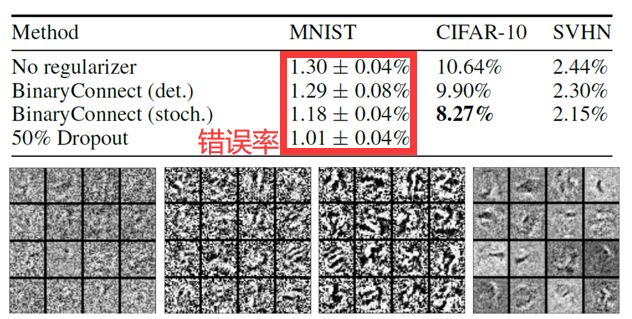
在论文中,该方法得到的模型比正常的神经网络模型表现更好,如下图。对于权重限制为+1或者-1,相当于加上了正则化。
Architecture Design
Low rank approximation
对于一个全连接层,可以通过添加一层 l i n e a r linear linear(线性层)来减少参数的个数。
如对于下图的普通全连接层,中间的权重矩阵的参数个数为: N × M N\times M N×M个。若 N N N和 M M M都是很大的一个数,那么 W W W矩阵将会很耗费内存空间。
接下来在中间加上一个 l i n e a r linear linear(没有激活函数)如下图;
假设 l i n e a r linear linear的维度是 K K K。此时的参数个数为: M × K + K × N M\times K+K\times N M×K+K×N。因为 K < M , N K

该方法将 W W W近似的转换成一个 U U U和一个 V V V矩阵的乘积,即 W ≈ U ∗ V W≈U* V W≈U∗V。
但因为 r a n k ( A B ) ≤ m i n ( r a n k ( A ) , r a n k ( B ) ) rank(AB)≤min(rank(A),rank(B)) rank(AB)≤min(rank(A),rank(B)),所以 r a n k ( W ) ≥ r a n k ( U ∗ V ) rank(W)≥rank(U*V) rank(W)≥rank(U∗V),这表示原来的全连接层能够表示更大的解空间,而添加线性层后只能表示小一些的空间了;即部分信息的丢失,这可能会对模型性能造成影响。
Depthwise Separable Convolution
C N N CNN CNN的卷积可以分成两步,从而减少参数个数。
首先先看常规的卷积操作:
- 卷积核的通道数要与输入的通道数一致
- 卷积核的个数即输出的通道数
如下图,假设有4个 3 × 3 × 2 3\times 3 \times 2 3×3×2的卷积核,参数个数为: 3 × 3 × 2 × 4 = 72 3\times 3 \times 2 \times 4=72 3×3×2×4=72

Depthwise Separable Convolution将卷积分成 D e p t h w i s e C o n v o l u t i o n Depthwise\ Convolution Depthwise Convolution和 P o i n t w i s e C o n v o l u t i o n Pointwise\ Convolution Pointwise Convolution两个步骤。
第一步: D e p t h w i s e C o n v o l u t i o n Depthwise\ Convolution Depthwise Convolution
D e p t h w i s e C o n v o l u t i o n Depthwise\ Convolution Depthwise Convolution要求:
- 卷积核的数量=输入的通道数
- 每个卷积核只考虑输入的一个通道
- 卷积核是一个 k × k k\times k k×k的矩阵
- 通道之间没有交互
如下图,每个 f i l t e r filter filter只会在一个通常上做点积,浅蓝色只负责在浅灰色的通道上做卷积,深蓝色的只负责在深蓝色的通道上做卷积。
因为输入的通道数是 2 2 2,所以这里只有两个 f i l t e r filter filter,分别负责一个输入通道。对于 6 × 6 × 2 6\times 6\times 2 6×6×2的输入数据,使用 3 × 3 3\times 3 3×3的卷积核进行 D e p t h w i s e C o n v o l u t i o n Depthwise\ Convolution Depthwise Convolution,输出是 4 × 4 × 2 4\times 4\times 2 4×4×2的矩阵。
第二步: P o i n t w i s e C o n v o l u t i o n Pointwise\ Convolution Pointwise Convolution
使用 4 4 4个 1 × 1 × 2 1\times 1\times 2 1×1×2的 f i l t e r filter filter对 D e p t h w i s e C o n v o l u t i o n Depthwise\ Convolution Depthwise Convolution的输出做标准的卷积。
4 4 4个 1 × 1 × 2 1\times 1\times 2 1×1×2的 f i l t e r filter filter:
- 4 4 4为输出通道的个数
- 1 × 1 1\times 1 1×1表示做 1 × 1 1\times 1 1×1的卷积操作
- 2 2 2为输入的通道数
如下图:
对于 4 × 4 × 2 4\times 4\times 2 4×4×2使用 4 4 4个 1 × 1 × 2 1\times 1\times 2 1×1×2做卷积后,得到 4 × 4 × 4 4\times 4\times 4 4×4×4的输出矩阵,和原来标准卷积的输出维度一致。
标准卷积与Depthwise Separable Convolution的比较:
标准的卷积可以看作:
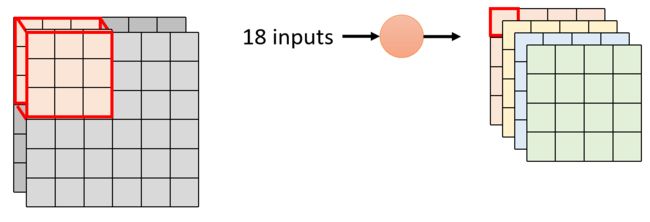
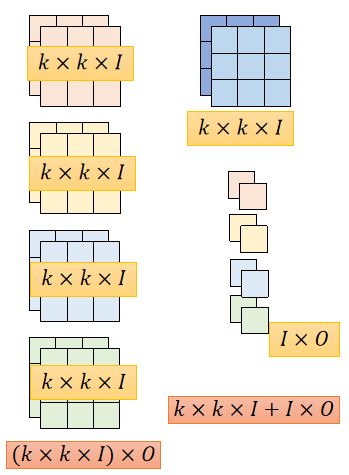
对于 3 × 3 × 2 3\times 3\times 2 3×3×2的卷积核可以看作是一个神经结点(卷积核的值即权重),总共 O = 4 O=4 O=4个卷积核,每个“神经结点”都要接收 k × k = 18 k\times k=18 k×k=18个 i n p u t s inputs inputs。对于其中一个卷积核的输出可以表示成下图;则标注卷积的参数维度是 k × k × I × O k\times k\times I \times O k×k×I×O
- k k k: k × k k\times k k×k的 f i l t e r filter filter
- I I I:输入的通道数
- O O O:输出的通道数
对于Depthwise Separable Convolution可以看作:
输出矩阵的第一个通道的左上角的元素,是由 D e p t h w i s e C o n v o l u t i o n Depthwise\ Convolution Depthwise Convolution输出结果的左上角的元素与 1 × 1 × 2 1\times 1\times 2 1×1×2的 f i l t e r filter filter做卷积得来的,而 D e p t h w i s e C o n v o l u t i o n Depthwise\ Convolution Depthwise Convolution输出结果是由输入矩阵与 2 2 2个 k × k k\times k k×k的 f i l t e r filter filter做点积得来的;如下图。
每个卷积核都看作一个神经元,可将上述过程抽象成下图:
Depthwise Separable卷积参数数量为: k × k × I + I × O k\times k\times I+I\times O k×k×I+I×O
标准卷积和Depthwise Separable卷积参数示意图如下:
左侧为标注卷积参数,右侧为Depthwise Separable卷积参数
将两者的参数数量做比值:
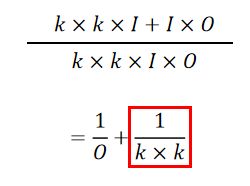
因为 O O O通常都比较大,所以着重关注 1 k × k \frac{1}{k\times k} k×k1。所以使用Depthwise Separable卷积参数数量缩小了 1 k × k \frac{1}{k\times k} k×k1倍。
Dynamic Computation
该方法的思想是:
如果当前设备的资源充足,如手机电源充足,那么算法就尽量做到最好,如使用更好的模型、训练的轮次更多些。
如果当前资源有限,如当前手机电量不足,那么算法可以减少运算量,算出一个还算过的去的输出结果。
该方法可行的方案有两种:
方案一:$ Train\ multiple\ classifiers$
训练多个模型,当资源不足的时候使用计算代价较小的模型进行运算,资源充足时使用最优的模型进行运算。
但多个模型意味着很多的参数,内存代价很大。
方案二: C l a s s i f i e r s a t t h e i n t e r m e d i a l a y e r Classifiers\ at\ the\ intermedia\ layer Classifiers at the intermedia layer
使用中间层输出,如我们在做分类任务时,可以在模型中间穿插一些 C l a s s i f i e r s Classifiers Classifiers,即只基于前几层的提取到的特征作为预测结果;如下图:
- 只使用前几层提取的特征做预测,预测的效果往往会不太好。
因为前几层可能只是提取了一些抽象、非具体的特征,用这些特征做预测并不能的到很好的效果。 - 由于中间接了 C l a s s i f i e r Classifier Classifier,会影响最终的分类结果,因为在训练的时候中间层就想要做分类,所以模型会促使参数在第一层就抽取一些具体的特征,从而导致部分具体特征的丢失,这样会使得后面的结果变差。