Spatiotemporal Adaptive Gated Graph Convolution Network for Urban Traffic Flow Forecasting
Spatiotemporal Adaptive Gated Graph Convolution Network for Urban Traffic Flow Forecasting
1.文章概述
当前方法不足:
- 交通数据实时变换,但大多数方法使用预定义图
- 道路的语义相似性没被考虑到
创新点:
- 通过寻找道路节点的空间邻域和语义邻域来构造动态加权图
- 多头自注意时间卷积网络被用来捕获历史观测中的局部和远程时间依赖关系
- 提出了一种自适应图门控机制
2. 问题定义
[ X t − T + 1 , ⋯ , X t ; G ] ⟶ f ( ⋅ ) [ X t + 1 , ⋯ , X t + M ] \left[\mathrm{X}^{t-T+1}, \cdots, \mathrm{X}^{t} ; \mathcal{G}\right] \stackrel{f(\cdot)}{\longrightarrow}\left[\mathrm{X}^{t+1}, \cdots, \mathrm{X}^{t+M}\right] [Xt−T+1,⋯,Xt;G]⟶f(⋅)[Xt+1,⋯,Xt+M]
给出前T个历史观察数据预测之后M个预测结果。
- Spatial Neighbor Subgraph
A i j s p = { 1 , v i and v j share the same intersection, 0 , otherwise A_{i j}^{s p}= \begin{cases}1, & v_{i} \text { and } v_{j} \text { share the same intersection, } \\ 0, & \text { otherwise }\end{cases} Aijsp={1,0,vi and vj share the same intersection, otherwise
- Semantic Neighbor Subgraph
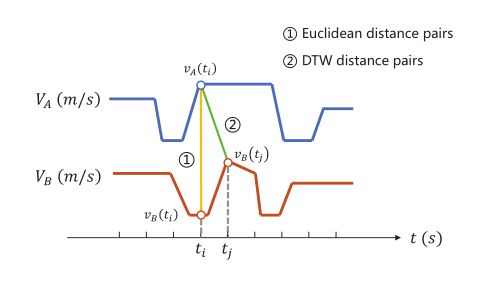
使用DTW算法计算两个时间序列的相似度,这里使用DTW算法是因为DTW算法计算的是两个序列距离并不是基于欧式距离的:
如上图所示,可以发现DTW算法所计算出来的距离更时候表示两个时间序列的相似度
语义邻接矩阵定义如下:
A i j s e = { 1 , DTW ( v i , v j ) > ϵ 0 , otherwise A_{i j}^{s e}= \begin{cases}1, & \operatorname{DTW}\left(v_{i}, v_{j}\right)>\epsilon \\ 0, & \text { otherwise }\end{cases} Aijse={1,0,DTW(vi,vj)>ϵ otherwise
3. 模型
模型框架如上所示,由三部分组成:自注意时间卷积网络、自适应门控图卷积网络和时空融合层
3.1 Self-Attention TCN
潜在子空间学习过程可以表示为:
Q = X W Q , K = X W K , V = X W V Q=X W^{Q}, \quad K=X W^{K}, \quad V=X W^{V} Q=XWQ,K=XWK,V=XWV
注意力计算公式如下:
Attention ( Q , K , V ) = softmax ( Q K T d k ) V \text { Attention }(Q, K, V)=\operatorname{softmax}\left(\frac{Q K^{T}}{\sqrt{d_{k}}}\right) V Attention (Q,K,V)=softmax(dkQKT)V
本文使用多头注意力机制:
MultiHead ( Q , K , V ) = Concat ( head 1 , … , head h ) W O where head i = Attention ( Q i , K i , V i ) \begin{aligned} \text { MultiHead }(Q, K, V) &=\text { Concat }\left(\text { head }_{1}, \ldots, \text { head }_{h}\right) W^{O} \\ \text { where head }_{i} &=\text { Attention }\left(Q_{i}, K_{i}, V_{i}\right) \end{aligned} MultiHead (Q,K,V) where head i= Concat ( head 1,…, head h)WO= Attention (Qi,Ki,Vi)
多头注意力网络的计算结果作为TCN网络的输入,其中TCN网络对于时刻t的节点i在p通道上TCN可以表示为:
y i , t , p = ∑ k = 1 K τ ∑ m = 1 M w k , m , p ⋅ x i , t − d ( k − 1 ) , m y_{i, t, p}=\sum_{k=1}^{K_{\tau}} \sum_{m=1}^{M} w_{k, m, p} \cdot x_{i, t-d(k-1), m} yi,t,p=k=1∑Kτm=1∑Mwk,m,p⋅xi,t−d(k−1),m
其中d为卷积扩张率, w k , m , p w_{k,m,p} wk,m,p是卷积核的元素。对整个TCN可表示为:
Y t c n = W ∗ d X \mathcal{Y}_{t c n}=\mathcal{W} *_{d} X Ytcn=W∗dX
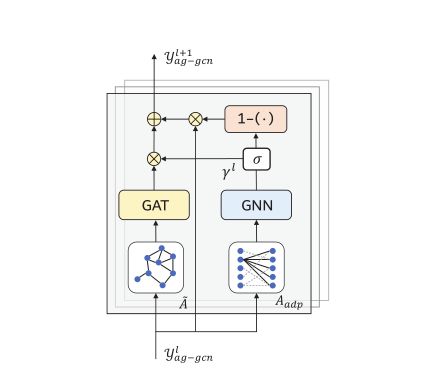
3.2 Adaptive Gated Graph Convolution Network (AG-GCN)
网络总框架中有两个AG-GCN模块,其差别在于输入数据一个是基于距离的关联矩阵,一个是基于语义信息的矩阵。在AG-GCN模块中,使用了两种不同的图形卷积方法,并使用一种自适应的图形门控机制将两种图形卷积的结果整合在一起,以实现知识的选择性更新和遗忘
-
Multi-head Graph Attention Network
该模块输入数据为: h = h 1 , h 2 , … , h N ∈ R D h={h_1,h_2,\ldots,h_N}\in R^D h=h1,h2,…,hN∈RD,输出为: h ′ = h 1 ′ , h 2 ′ , … , h N ′ ∈ R M h^{'}={h^{'}_1,h^{'}_2,\ldots,h^{'}_N}\in R^M h′=h1′,h2′,…,hN′∈RM
首先节点通过共享线性变换和多头注意力机制计算两节点之间的注意力系数:
e i j = a ( W h i , W h j ) , j ∈ N i e_{i j}=a\left(W h_{i}, W h_{j}\right), j \in \mathcal{N}_{i} eij=a(Whi,Whj),j∈Ni
α i j = softmax j ( e i j ) = exp ( e i j ) ∑ k ∈ N i exp ( e i k ) \alpha_{i j}=\operatorname{softmax}_{j}\left(e_{i j}\right)=\frac{\exp \left(e_{i j}\right)}{\sum_{k \in N_{i}} \exp \left(e_{i k}\right)} αij=softmaxj(eij)=∑k∈Niexp(eik)exp(eij)
K个独立的注意力机制结果concatenate形成最后的结果。
- Adaptive Graph Gating Mechanism
为了防止出现过平滑问题,本文提出了自适应图门控机制,此次使用两个可学习向量 E s , E t E_s,E_t Es,Et,获得自适应邻接矩阵:
A a d p = softmax ( ReLU ( E s E t T ) ) A_{a d p}=\operatorname{softmax}\left(\operatorname{ReLU}\left(E_{s} E_{t}^{T}\right)\right) Aadp=softmax(ReLU(EsEtT))
然后利用自适应邻接矩阵计算图形卷积的结果,得到门阈值 γ \gamma γ
γ = σ ( A a d p X Θ ) \gamma=\sigma\left(A_{a d p} X \Theta\right) γ=σ(AadpXΘ)
阈值 γ \gamma γ用来控制这一层保留多少信息, 1 − γ 1-\gamma 1−γ表示在下一层中忘记该层多少信息,并使用多少上一层的结果
y a g − g c n l = { X , l = 0 , γ l ⊙ g ( Z l ) + ( 1 − γ l ) ⊙ y a g − g c n l − 1 , l = 1 , 2 , … , L y_{a g-g c n}^{l}= \begin{cases}X, & l=0, \\ \gamma^{l} \odot g\left(Z^{l}\right)+\left(1-\gamma^{l}\right) \odot y_{a g-g c n}^{l-1}, & l=1,2, \ldots, L\end{cases} yag−gcnl={X,γl⊙g(Zl)+(1−γl)⊙yag−gcnl−1,l=0,l=1,2,…,L
3.3 Spatiotemporal Fusion Network
在获得时间、空间和语义域的高维特征后,如何聚合时空信息进行多步预测,本文探讨了三种融合机制机制:级联机制、最大池机制和LSTM注意机制
- Concatenation: c o n c a t e n a t e [ h i t p , h i s p , h i d t w ] concatenate[h_{i}^{t p}, h_{i}^{s p}, h_{i}^{d t w}] concatenate[hitp,hisp,hidtw],最直接保留最多原始时空特征
- Max-pooling: m a x [ h i t p , h i s p , h i d t w ] max[h_{i}^{t p}, h_{i}^{s p}, h_{i}^{d t w}] max[hitp,hisp,hidtw]
- LSTM-attention:
预测方法:
- auto-regressive prediction method
- Direct Multi-step Prediction