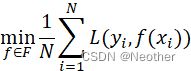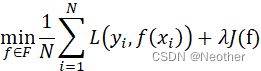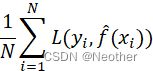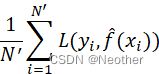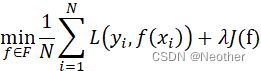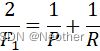第一章 统计学习方法概论

第一节 导论

一、监督学习

实现步骤

    （1）有限的训练数据集合（数据有label/有标注的数据）

    （2）确定模型的假设空间（所有的备选模型）

    （3）确定模型选择的准则（学习策略）

    （4）实现求解最优模型的算法

    （5）通过学习方法选择最优模型

    （6）利用最优模型对新数据进行预测或分析

二、统计学习的三要素

1、模型（假设空间）

1. 决策函数

F={f|Y=fθx,θ∈Rn}

1. 条件概率分布

P={P|PθY|X,θ∈Rn}

（Θ表示的某一个模型）

2、策略

损失函数——计算模型预测结果和实际结果的差距。几种损失函数：

1. 0-1损失函数

L(Y,f(X))=1,Y≠f(X)0,Y=f(X)

1. 平方损失函数

LY,fX=(Y-f(X))2

1. 绝对损失函数

LY,fX=|Y-f(X)|

1. 对数损失函数

LY,P(Y|X)=-log⁡P(Y|X)

1. 经验风险最小化

minf∈F1Ni=1NL(yi,f(xi))

1. 结构风险最小化

minf∈F1Ni=1NLyi,fxi+λJ(f)

        J(f),正则化，防止过拟合

3、算法

三、模型的评估与选择

训练误差（针对训练数据集）

1Ni=1NL(yi,f(xi))

测试误差（针对测试数据集）

1N'i=1N'L(yi,f(xi))

验证集

四、正则化与交叉验证

1. 结构风险最小化 正则化

minf∈F1Ni=1NLyi,fxi+λJ(f)

        J(f),正则化，防止过拟合

1. 交叉验证

数据集随机划分为3个部分：

    训练集

    测试集

    验证集

五、泛化能力

泛化误差上界

（1）介绍

泛化误差：

    一个机器学习模型的泛化误差（Generalization error），是一个描述学生机器在从样品数据中学习之后，离教师机器之间的差距的函数。使用这个名字是因为这个函数表明一个机器的推理能力，即从样品数据中推导出的规则能够适用于新的数据的能力。

泛化误差上界：

    泛化误差上界可理解为模型学习能力的“出错上限”，显然，当样本容量趋于无穷大时，泛化误差上界趋于0

（2）定理

    在二分类问题中，若假设空间为有限个函数的集合F=f1,f2,…,fd, 对于任意的f∈F,至少以概率1-δ，以下不等式成立：

Rf≤Rf+ϵ(d,N,δ)

其中，

Rf=ELY,fX:泛化误差（测试集上的期望风险）

Rf=1Ni=1NL(yi,f(xi))：训练集上的经验风险

ϵd,N,δ=12N(logd+log1δ)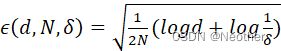:泛化误差与样本数量N成正比，与假设空间包含的函数数量d成反比。当样本数量越大时，泛化误差上界越小；当假设空间F包含的函数越多，泛化误差上界越大。

    （3）证明

    证明利用了Hoeffding不等式：

设Sn=i=1NXi,是独立随机变量X1,X2,…,Xn之和，Xi∈[ai,bi],则对任意t>0，以下不等式成立：

P(E(Sn)-Sn≥t)≤exp⁡(-2t2i=1n(bi-ai)2)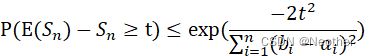

    ∵X=Snn  N=n

P(ESnn-Snn≥tn)≤exp⁡(-2(nt)2i=1n(bi-ai)2)

                   (不等式右边采用变量替换 t0=tn t=nt0)

    化简得：

P(E(Xn)-X≥t)≤exp⁡(-2n2t2i=1n(bi-ai)2)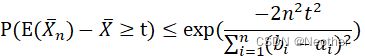

    在二分类问题中，显然ai=0，bi=1，上式可写为：

P(Rf-Rf≥ε)≤exp⁡(-2Nε2)

    从假设空间的全部函数上看，上式可写为：

P∃f∈F:Rf-Rf≥ε=P∪f∈F{Rf-Rf}≥ε≤dexp⁡(-2Nε2)

    考虑对立事件。对任意f∈F， 有：

PRf-Rf<ε≥1-dexp⁡(-2Nε2)

    令：

δ= dexp⁡(-2Nε2)

综上，至少以概率1-δ有Rf≤Rf+ϵ(d,N,δ)成立。

六、生成模型和判别模型

生成方法：PYX=P(X,Y)P(X)

判别方法：f(X)或者P(Y|X)

七、分类问题

评价指标

TP:将正类别预测为正类别

FN:将正类别预测为负类别

FP: 将负类别预测为正类别

TN: 将负类别预测为夫类别

精确率：预测为正类的样本中有多少是被分对的。

P=TPTP+FP

召回率：正类的样本中有多少是被预测为正类的。

R=TPTP+FN

F1值：

2F1=1P+1R

第二节 极大似然估计

极大似然估计：利用已知的样本结果信息，反推最具有可能（最大概率）导致这些样本结果出现的模型参数值。——“模型已定，参数未知”。（已知某个随机样本符合某种概率分布，但是其中某个具体参数θ不清楚，通过极大似然估计得到θ，该θ使这个随机样本出现的概率最大。

1、举例说明：

在0-1问题中，为1的概率是θ

（1）概率函数   

PX=x=θx(1-θ)1-x

（2）似然函数  

Lθ=PX1=x1θ…PXn=xnθ=i=1nθxi(1-θ)1-xi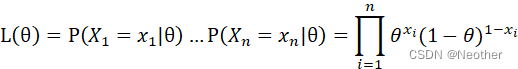

    为了防止下溢问题，改为求解对数函数:

maxlnLθ=i=1nx1lnθ+(1-x1)ln(1-θ)

    求导数:

∂lnLθ∂θ=i=1nx1θ-n-i=1nx11-θ=0

    估计值：

θ=i=1nx1n

当估计值（参数）是上述所求值时，出现已知现象的概率最大。

2、推广

（1）概率密度函数f(x)

（2）目标函数maxLθ=i=1nf(xi) 

（3）对似然函数取对数 maxlnLθ

（4）对θ求偏导数  ∂lnLθ∂θ

（5）解似然方程（组）  ∂lnLθ∂θ=0

第三节 梯度下降法

1、算法思路

输入：目标函数f(x),梯度函数gx=∆fx,计算精度ε，步长η。

输出：f(x)的极小值点x*。

(1)取初始值x0∈Rn,置k=0

(2)计算f(xk)

(3)计算梯度gk=g(x(k)),当gk<ε时，停止迭代，否则，xk+1=xk-η*gk,重新转至步骤(2)

2、总结

（1）梯度下降法在每一步时计算当前位置的梯度由此明白该往什么方向走能够使函数值下降。

（2）参数步长（0~1）决定了每步走的幅度。