【论文理解】Uncertainty-Aware Few-Shot Image Classification

---

前言

这篇论文是10月9号挂在arxiv上的，作者来自中科大。论文在少样本图像分类算法方面提出了一个独特的改进角度，个人认为比较有意思。我在读完之后，想要把论文的思想以及自己的理解记录下来，供大家参考。如有错误请大家指出哦~ 阅读本博文前，你可能需要掌握一些少样本学习的基本概念。

查看原文，请点这里。 博文中的图片来源于原文~

一、文章目的

1.背景

这篇论文的研究领域属于少样本图像分类，研究基础是基于度量学习的少样本学习算法。论文的改进算法依托于Prototype Net（一种基本的度量学习算法）的基本思想，即将support set中每一类图像的特征取均值，作为该类的类特征（prototype）。再计算query图像的特征和各个prototype的相似度（similarity），并将query分到相似度最大的那类。

这种度量方法也取得了很好的分类效果，但是作者发现这其中存在一个问题：观测噪声（observation noises）。

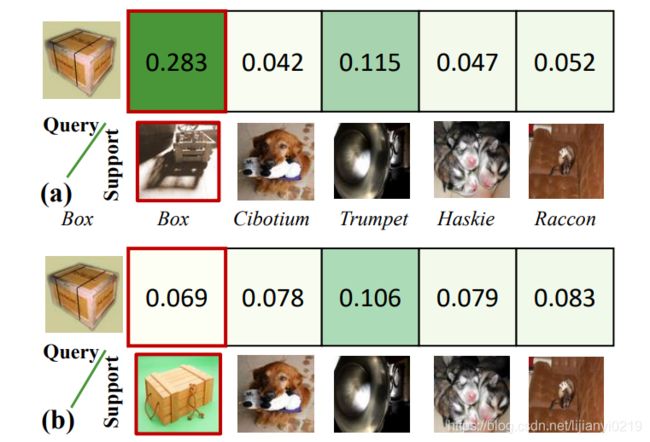
由于一个少样本分类任务中，query及support图像的质量参差不齐，可能有些query和support图像明明属于同一类，但由于拍摄角度不好或物体本身比较奇特，他们的外观就是差的比较多，比如下面这两张对比图：

同样是盒子，(a)中query和support的外观就差的远，(b)中二者就差不多。
那么外观相差大的图像的特征相似度比较低，但这两张图像确实属于同一类，因此这时就认为计出的相似度值的可信度低。反之，当同一类的两张图象外观接近时，他们的特征相似度高，这时计算得到的相似度的可信度就高。

这样就会带来一个观测噪声，它是由输入图像的质量来决定的。也就是说，我们计算获得的相似度的值是带有噪声的，我们不能完全相信这个值。它存在一个可信度，这个可信度根据输入图像的特点会有相应变化， 上图中(b)情况下获得的相似度的可信度就高，(a)情况下可信度就低。

那么问题来了，我们要怎么降低观测噪声对结果的影响呢？这就是作者要告诉我们的了。

2.目的

其实上面的这句话就是本文的目的：降低观测噪声在度量学习中的副作用。 它采用的途径是改进训练阶段的损失函数，使得损失函数就考虑到噪声的影响。这样在改进的损失函数下训练，就可以获得一个能更好应对observation noises的度量模型。即在不同质量的输入下，都具有很好鲁棒性的模型。

二、核心思想

前面我们了解到，由于observation noises的存在，相似度值是具有可信度的，那么我们在训练过程中，计算损失的时候就不能完全使用计算得到的相似度值，而是要根据其可信度去调整这个值。
当然了，为了“不在一棵树上吊si”，我们最好按照概率多取几个这样的调整值作为参考，共同计算损失。

这样，相当于将原来确定的相似度值，转换为了随机变量，并且使用在其概率分布下采样的值计算损失。这样获得的损失对相似度值具有统计意义，用来训练可以有效减轻observation noises的副作用。 这就是文章的关键点。
看到这里，我们就需要解决两个问题：

1. 如何获得相似度值的概率分布？
2. 如何进行采样？如何使用该分布下的多个采样值共同计算损失？

于是，我们来论文算法中寻找答案。

三、论文算法

1.基础框架

在讲解论文的改进算法前，我们先来介绍论文是基于哪种度量学习算法改进的。
作者的改进只在前期训练阶段进行，对训练时的损失函数进行了调整。之后的测试阶段没有任何改动。 我们就介绍一下前期训练阶段使用的baseline。

作者参考一篇新论文A new meta-baseline for few-shot learning的思想，在预训练时采用两个子阶段：

• Stage-1 基于分类的预训练，即在base classes上用分类任务训练网络，不过网络最后端的分类层按照cosine的方式计算相似度，取最大相似度对应的类别作为输出类别。因此最后分类层的权重可以看作prototypes。
• Stage-2 元学习，这一阶段就是常规的少样本学习的元训练算法了，我们以人造的假任务（FSL task）作为训练样本，在假任务的query set上计算损失。这里的网络框架和prtotypical net一样，通过计算类prototypes与query特征的相似度进行分类。

2.获得分布

简单起见，我们假设一张quey图像和某个类prototype的相似度值的分布符合高斯分布，即：

$z_i$表示一张query图像$x_i$的特征，$C$表示support set中$N$个类别的prototypes。
$s_{ij}$表示第$i$张query图像和第$j$类prototype的相似度。

分布的均值我们可以直接计算出来：（这是个向量内积）

方差如何计算呢？它可是非常重要的值，代表着这个$s_{ij}$的可信度，作者称之为uncertainty，即不确定度，记为${\sigma }_{ij}$。

3.计算方差

(1).确定方法

对于query图像$x_i$的分类结果，是由它和所有类特征的相似度值计算得到的，即

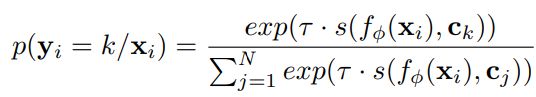
这个式子的计算结果表示图像$x_i$属于第$k$类的概率值，再用这个值计算CE损失。

因此，当我们计算$x_i$和某一类特征$c_j$的相似度的不确定度时，要综合考虑$x_i$和其他类特征的相似度值，共同计算出结果。这时，我们就可以采用图神经网络。
图神经网络的一大特点就是能加权融合不同节点的特征，符合要求。

(2).图卷积求解

文中作者采用了基本的GCN。

建图

首先明确，一张graph代表的是 一个query图像$x_i$和全部类特征 间相似度值及关系。

节点： 每个节点$v_{ij}$特征表示$x_i$和每个类特征$c_j$的相似度。由于一般方法计算出的相似度是一个标量，不适合作为一个节点的特征，我们就把它进行扩展，对$x_i$特征和$c_j$进行分段，再对每一段都计算一个相似度，最后组合成一个向量，作为节点特征。这里分成$L$段，每段相似度表示为$r_{ij}^l$。

边： 以边连接的两节点特征的相似度作为这条边的权重，最终可以获得一个邻接矩阵。

图卷积

这个过程和一般的GCN一样，本质都是根据邻接矩阵去融合节点信息。$G_i$表示规范化的邻接矩阵；$W_{..}$表示网络参数。


最终GCN输出的节点特征是一维的，即每个节点输出一个标量值，${\mathbf{u}}_i$的第$j$个值就是前面提到的不确定度${\sigma }_{ij}$。

这样，我们就获得了每个相似度值的不确定度。接下来需要利用这个不确定度去改进损失函数啦！

4.基于不确定度的优化

通常情况下，我们对一个query计算CE损失时，会直接根据计算得到的相似度值计算出一个结果，作为其损失。
现在，为了实现损失在相似度值上的统计性，我们依据前面获得的相似度分布，计算损失在相似度上的期望。但由于在这么多分布上计算积分太过复杂，我们通过蒙特卡洛采样的方式，获取$T$个符合分布的相似度值，对这些值计算其损失，再求损失均值，就可以近似于对于相似度的概率分布求了期望。

最终一张query图像$x_i$损失的形式变为：

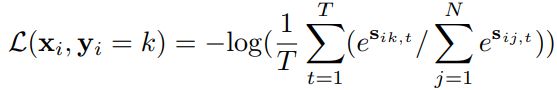
这里为了使得采样值是可微的，作者采用了re-parameterizing的方法，即先在标准正态分布上采样一个中间值，再利用统计学中的性质获得符合相似度分布的采样值：

以上四部分即概括了论文的全部（应该是的吧==）算法思想，大家可以结合其核心思想再做思考~

整体框图如下：

四、实验结果

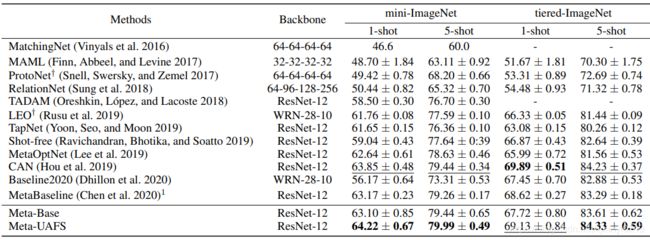
这里我就放一张总的实验结果，作者还做了一些对比实验，有兴趣的话可以去原文查阅。

总的来说，使用两阶段的预训练比单使用其中一阶段的效果要好；训练时加入不确定性的考虑能提升算法性能。

下面的图就直观表现了不确定值的意义，当query和同类support的外观差距大时，获得的相似度的不确定值就高，也就是可信度低。

---

总结

这篇论文的核心就是要通过将度量学习中的相似度值由确定值变为随机变量，来减轻输入图像observation noises带来的副作用。

我想来谈一下我认为的，作者设计的损失函数能减缓这种副作用的原因。
当query图像和它对应的support set中的类特征相差较远时，计算得到的相似度会很低，那么这张query产生的损失会很大。可以任务这个损失是带有噪声的，即观测噪声。这种损失可能会极大拉偏梯度下降的方向，使得训练不易收敛。
那么，给定相似度一个概率分布，我们在这个分布上采样，可能会将这个相似度调整的更符合实际，也可能获得一个更离谱的相似度。但没关系，我们对他们的损失值求平均，获得统计结果。这样在训练的时候，可以一定程度上弱化原来不合理的相似度带来的噪声，减少梯度下降方向的偏移度，更有利于训练。

文章中还有一段对于Deep Learning不确定度的分类描述，个人想要收藏一下，就列在这里：

For deep neural network, there are two main types of uncertainty that can be modeled: aleatoric uncertainty, and epistemic uncertainty . Epistemic uncertainty captures model-related stochasticity, including parameters choices, architecture, etc. Aleatoric uncertainty captures the noise inherent in the observations (Kendall and Gal 2017; Gal 2016; Kendall, Gal, and Cipolla 2018). The aleatoric uncertainty can be further divided into two sub-categories. Heteroscedastic uncertainty, as a sub-category of aleatoric uncertainty, is data-dependent, which depends on the input data of the model, with some noisy inputs or rarely seen inputs potentially having lower confidence on the output/prediction. For per-pixel semantic segmentation and depth regression tasks, input-dependent heteroscedastic uncertainty are considered as loss attenuation for better optimization . In contrast, homoscedastic uncertainty is a quantity which is the same for all input data and varies between different tasks. It is thus also described as task-dependent uncertianty. It has been adopted in weighting the loss function for multi-task learning.
论文中描述的不确定度属于Heteroscedastic uncertainty，是依赖于数据的。