EM算法和变分自编码器（VAE）的联系

两种常用的推断方法：期望最大化算法（Expectation Maximaization, EM)和变分自编码器（Variational autoencoders, VAE），都是可以通过近似逼近来优化目标函数。直观上来说，在优化目标函数上，EM是在可能的模型中交替寻找最大化，而VAE是根据梯度的采样估计进行梯度下降。那么他们之间是否有一些联系呢？今天我们来探索下。

EM算法简介

EM算法是一种含有隐变量的模型中搜索参数的最大似然估计或最大后验估计的算法。也就是说，它可以用来估计含有隐变量的概率分布中的未知参数。

给定观察数据集$X$，隐变量数据或缺失值$Z$，和未知的参数$\theta$，EM算法迭代更替下面两步：
E步（Expectation）：计算期望，给定$X$和当前参数${\theta }^{(}t)$的估计值，计算关于当前$Z$的条件分布的对数似然函数：
$$Q(\theta \mid {\theta }^{(t)})=E_{Z\mid X,{\theta }^{(}t)}[log\mathcal{L}(\theta ;X,Z)]$$
M步（Maximaization）：寻找使得似然函数最大化的参数：
$${\theta }^{(t+1)}={\mathrm{argmax}}_{\theta }Q(\theta \mid {\theta }^{(t)})$$
M步学习到的参数估计值又被用于下一个E步的估计，这个过程不断地交替着，直到收敛为止。

VAE算法简介

VAE是2014年由Kingma和Welling在深度学习的背景下提出的。自编码器跟压缩（compression）相关。如下图所示，JPEG将图像压缩为编码形式，这样可以使用较少的内存，我们可以解压缩来恢复图像，但会丢失一些分辨率。

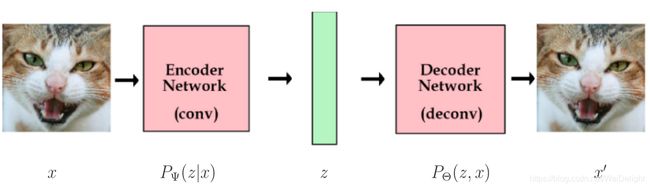
从信息论上来说，压缩比较贴近于对分布的建模。香农的源编码定理（Shannon’s source coding theorem）阐释了对于任意的概率分布，例如，在“自然”图像上的分布，可以使用每个元素的多个比特（bits）来对元素进行编码，这等价于信息理论中分布的熵。在上图中，中间压缩形式的平均比特数应该等于图像上概率分布的熵。

但是变分自编码器并没有直接解决压缩问题，而是侧重于拟合分布$P_{\Theta }(z,x)$中的参数$\Theta$，从而最大化给定样本集$x$（比如一些点的集合或者一组图像集合）的边缘概率$P_{\Theta }(x)$。编码仅仅是一个工具来更有效地拟合这些参数。

EM和VAE的联系

从上面的介绍，我们可以直到，VAE解决的问题跟EM解决的问题是一样的：都是在给定含有隐变量的模型对应的数据下，拟合概率分布的参数。具体来说，EM和VAE都是根据$P_{\Psi }(z\mid y)$(编码)和$P_{\Theta }(y,z)$（定义了P(z)和P(y\mid z)的模型）这两个分布的目标函数而制订的：
$$\begin{gathered} {\Psi }^{\ast },{\Theta }^{\ast }={\mathrm{argmax}}_{\Psi ,\theta }\sum _y\mathcal{L}(\Psi ,\Theta ,y)， \\ \mathcal{L}(\Psi ,\Theta ,y)=E_{z\sim P_{\Psi }(z\mid y)}\ln P_{\Theta }(z,y)+H(P_{\Psi }(z\mid y))(1) \\ =\ln P_{\Theta }(y)-KL(P_{\Psi }(z\mid y),P_{\Theta }(z\mid y))。(2) \end{gathered}$$
其中，$y$表示训练数据。公式（1）和（2）的等价性提供了目标函数的不同形式。这个等价性隐含在下面的式子中：

从EM角度

从上面式子可以看到，EM可以被定义为对${\sum }_y\mathcal{L}(\Psi ,\Theta ,y)$的迭代优化，公式（2）表示了对参数$\Psi$的优化（E步），公式（1）表示对参数$\Theta$的优化（M步）。EM适用于能精确有效地通过这两步的不断交替迭代估计得到的模型。对于估计到的模型中每个M步，EM保证提升${\sum }_y\ln P_{\Theta }(y)$的值。对于这些模型，这种交替优化的方式通常远远优于任何形式的对${\sum }_y\ln P_{\Theta }(y)$的梯度下降。

从VAE角度

VAE用于不能以闭集形式有效地进行交替优化的模型中。 VAE在公式（1）上进行梯度下降，其中通过从编码器采样来估计梯度。这通常涉及“重新参数化技巧（reparameterization trick）”。如果用$z=g_{\Psi (y,\eta )}$来表示$P_{\Psi }(z\mid y)$，其中$\eta$是固定分布的随机变量，那么，我们可以将公式（1）重写为：
$$\mathcal{L}(\Psi ,\Theta ,y)=E_{\eta }\ln P_{\Theta }(g_{\Psi }(y,\eta ),y)+H(P_{\Psi }(g_{\Psi }(y,\eta )\mid y))。(3)$$

常见的做法就是，将$P(\eta )$，$P_{\Psi }(z\mid y)$，$P_{\Theta }(z)$和$P_{\Theta }(y\mid z)$看成是所有高维的高斯分布，每个用均值和方差表示。在求$P_{\Psi }(z\mid y)$，$P_{\Theta }(z)$和$P_{\Theta }(y\mid z)$通过深度网络计算的均值和方差时，将噪声变量$\eta$看成是固定的零均值各向同性高斯分布。我们就可以给定任意$\eta$的样本下，计算公式（3）的梯度了。

学习资源

不同编程语言的VAE实现代码：
MATLAB https://github.com/peiyunh/mat-vae
Chainer https://github.com/pfnet/chainer/tree/master/examples/vae
Edward (Tensorflow) https://github.com/blei-lab/edward/blob/master/examples/vae.py
https://github.com/blei-lab/edward/blob/master/examples/vae_convolutional.py
Keras (Theano and Tensorflow) https://github.com/fchollet/keras/blob/master/examples/variational_autoencoder.py
Tensorflow https://github.com/y0ast/VAE-TensorFlow
Tensorflow https://jmetzen.github.io/2015-11-27/vae.html
Theano https://github.com/y0ast/Variational-Autoencoder
Torch https://github.com/y0ast/VAE-Torch

参考资料：

1. Expectation–maximization algorithm
2. Tutorial on Variational Autoencoders
3. VAE = EM