【深度学习实战】从零开始深度学习（五）：生成对抗网络——深度学习中的非监督学习问题

参考资料：

1. 《PyTorch深度学习》（人民邮电出版社）第7章 生成网络
2. PyTorch官方文档
3. 廖星宇著《深度学习入门之Pytorch》第6章 生成对抗网络
4. 其他参考的网络资料在文中以超链接的方式给出

1. 生成模型（Generative Model）

生成模型是指一些列用于随机生成可观测数据的模型，并使“生成”的样本和“真实”样本尽可能地相似。这个概念属于概率统计和机器学习。生成模型的两个主要功能就是学习概率分布P_model(X)和生成数据。

前面介绍的CNN和RNN等网络，大多应用于监督学习的任务，生成模型的目的之一就是希望能让无监督学习取得比较大的进展。

概率生成模型，简称生成模型（Generative Model），是概率统计和机器学习中的一类重要模型，指一系列用于随机生成可观测数据的模型 。生成模型的应用十分广泛，可以用来不同的数据进行建模，比如图像、文本、声音等。比如图像生成，我们将图像表示为一个随机向量X，其中每一维都表示一个像素值。假设自然场景的图像都服从一个未知的分布pr(x)，希望通过一些观测样本来估计其分布。高维随机向量一般比较难以直接建模，需要通过一些条件独立性来简化模型。深度生成模型就是利用深层神经网络可以近似任意函数的能力来建模一个复杂的分布。方法：从统计的角度表示数据的分布情况，能够反映同类数据本身的相似度；生成方法还原出联合概率分布，而判别方法不能；生成方法的学习收敛速度更快、即当样本容量增加的时候，学到的模型可以更快地收敛于真实模型；当存在隐变量时，仍可以用生成方法学习，此时判别方法不能用。 ——百度百科

这里我们介绍两个最简单的生成模型—— 自编码器（Autoencoder） 和 变分自编码器（Variational AutoEncoder）。

1.1 自编码器（Autoencoder）

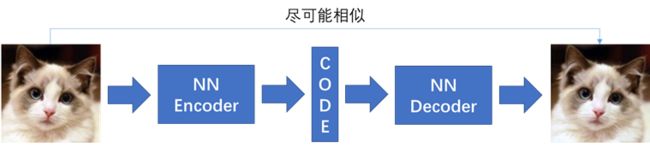
自编码器包括两个部分，第一部分是编码器(encoder)，第二部分是解码器(decoder)，编码器和解码器都可以是任意的模型，通常我们可以使用神经网络作为我们的编码器和解码器，输入的数据经过神经网络（NN Encoder）降维到一个编码（Code），然后又通过另外一个神经网络解码（NN Decoder）得到一个与原始数据一模一样的生成数据，通过比较原始数据和生成数据，希望他们尽可能接近，所以最小化他们之间的差异来训练网络中编码器和解码器的参数。

我们接下来可以使用PyTorch实现一个简单的自编码器

数据准备

我们还是使用MNIST手写数据集

im_tfs = tfs.Compose([
    tfs.ToTensor(),
    tfs.Normalize((0.1307,), (0.3081,)) 
])

train_set = MNIST('./mnist', transform=im_tfs, download=True)
train_data = DataLoader(train_set, batch_size=128, shuffle=True)

构建模型

我们定义一个简单的4层网络作为编码器，中间使用ReLU激活函数；解码器同样使用简单的4层网络，前面三层采用ReLU激活函数，最后一层采用Tanh函数。

class autoencoder(nn.Module):
    def __init__(self):
        super(autoencoder, self).__init__()
        
        self.encoder = nn.Sequential(
            nn.Linear(28*28, 128),
            nn.ReLU(True),
            nn.Linear(128, 64),
            nn.ReLU(True),
            nn.Linear(64, 12),
            nn.ReLU(True),
            nn.Linear(12, 3) # 输出的 code 是 3 维，便于可视化
        )
        
        self.decoder = nn.Sequential(
            nn.Linear(3, 12),
            nn.ReLU(True),
            nn.Linear(12, 64),
            nn.ReLU(True),
            nn.Linear(64, 128),
            nn.ReLU(True),
            nn.Linear(128, 28*28),
            nn.Tanh()
        )

    def forward(self, x):
        encode = self.encoder(x)
        decode = self.decoder(encode)
        return encode, decode

开始训练

net = autoencoder()
    
criterion = nn.MSELoss(size_average=False)
optimizer = torch.optim.Adam(net.parameters(), lr=1e-3)

def to_img(x):
    '''
    定义一个函数将最后的结果转换回图片
    '''
    x = 0.5 * (x + 1.)
    x = x.clamp(0, 1)
    x = x.view(x.shape[0], 1, 28, 28)
    return x

# 开始训练自动编码器
for e in range(100):
    for im, _ in train_data:
        im = im.view(im.shape[0], -1)
        im = Variable(im)
        # 前向传播
        _, output = net(im)
        loss = criterion(output, im) / im.shape[0] # 平均
        # 反向传播
        optimizer.zero_grad()
        loss.backward()
        optimizer.step()
    
    if (e+1) % 20 == 0: # 每 20 次，将生成的图片保存一下
        print('epoch: {}, Loss: {:.4f}'.format(e + 1, loss.data[0]))
        pic = to_img(output.cpu().data)
        if not os.path.exists('./simple_autoencoder'):
            os.mkdir('./simple_autoencoder')
        save_image(pic, './simple_autoencoder/image_{}.png'.format(e + 1))

我们看一下生成的图片，效果还是很不错的：

使用更复杂一点的网络

class conv_autoencoder(nn.Module):
    def __init__(self):
        super(conv_autoencoder, self).__init__()
        
        self.encoder = nn.Sequential(
            nn.Conv2d(1, 16, 3, stride=3, padding=1),  # (b, 16, 10, 10)
            nn.ReLU(True),
            nn.MaxPool2d(2, stride=2),  # (b, 16, 5, 5)
            nn.Conv2d(16, 8, 3, stride=2, padding=1),  # (b, 8, 3, 3)
            nn.ReLU(True),
            nn.MaxPool2d(2, stride=1)  # (b, 8, 2, 2)
        )
        
        self.decoder = nn.Sequential(
            nn.ConvTranspose2d(8, 16, 3, stride=2),  # (b, 16, 5, 5)
            nn.ReLU(True),
            nn.ConvTranspose2d(16, 8, 5, stride=3, padding=1),  # (b, 8, 15, 15)
            nn.ReLU(True),
            nn.ConvTranspose2d(8, 1, 2, stride=2, padding=1),  # (b, 1, 28, 28)
            nn.Tanh()
        )

    def forward(self, x):
        encode = self.encoder(x)
        decode = self.decoder(encode)
        return encode, decode

conv_net = conv_autoencoder()

criterion = nn.MSELoss(size_average=False)
if torch.cuda.is_available():
    conv_net = conv_net.cuda()
optimizer = torch.optim.Adam(conv_net.parameters(), lr=1e-3, weight_decay=1e-5)

我们使用一个更加复杂一点的网络——多层卷积神经网络构建编码器；解码器使用了nn.ConvTranspose2d()，相当于卷积的反操作。

我们可以对比下两个模型的训练效果：

可以看到，同样是训练40轮，卷积模型生成的图片更清晰一些。

1.2 变分自编码器（Variational AutoEncoder，VAE）

变分自编码器是自动编码器的升级版本，它的结构和自动编码器非常相似。与自动编码器不同的是，在编码过程中增加一些限制，使其生成的隐含向量能够粗略地遵循一个标准正态分布；这样只要给它一个标准正态分布的随机隐含向量，通过解码器就能够生成想要的图片，而不需要先给它一张原始图片编码。

因此，我们的编码次每次生成的不是一个隐含向量，而是一个均值和一个标准差。

同样可以利用PyTorch实现变分自编码器的结构：

完整代码

reconstruction_function = nn.MSELoss(size_average=False)

def loss_function(recon_x, x, mu, logvar):
    """
    recon_x: generating images
    x: origin images
    mu: latent mean
    logvar: latent log variance
    """
    MSE = reconstruction_function(recon_x, x)
    # loss = 0.5 * sum(1 + log(sigma^2) - mu^2 - sigma^2)
    KLD_element = mu.pow(2).add_(logvar.exp()).mul_(-1).add_(1).add_(logvar)
    KLD = torch.sum(KLD_element).mul_(-0.5)
    # KL divergence
    return MSE + KLD

class VAE(nn.Module):
    def __init__(self):
        super(VAE, self).__init__()

        self.fc1 = nn.Linear(784, 400)
        self.fc21 = nn.Linear(400, 20) # mean
        self.fc22 = nn.Linear(400, 20) # var
        self.fc3 = nn.Linear(20, 400)
        self.fc4 = nn.Linear(400, 784)

    def encode(self, x):
        h1 = F.relu(self.fc1(x))
        return self.fc21(h1), self.fc22(h1)

    def reparametrize(self, mu, logvar):
        std = logvar.mul(0.5).exp_()
        eps = torch.FloatTensor(std.size()).normal_()
        if torch.cuda.is_available():
            eps = Variable(eps.cuda())
        else:
            eps = Variable(eps)
        return eps.mul(std).add_(mu)

    def decode(self, z):
        h3 = F.relu(self.fc3(z))
        return torch.tanh((self.fc4(h3)))

    def forward(self, x):
        mu, logvar = self.encode(x) # 编码
        z = self.reparametrize(mu, logvar) # 重新参数化成正态分布
        return self.decode(z), mu, logvar # 解码，同时输出均值方差

可以把VAE的结果和自动编码器的结果进行对比：

2. 生成对抗网络（Generative Adversarial Networks，GAN）

生成对抗网络由两部分组成——生成+对抗。第一部分是生成模型，类似自动编码器的解码部分；第二部分是对抗模型，可以看成是一个判断真假图片的判别器。生成对抗网络就是让两个网络相互竞争，通过生成网络来生成假的数据，对抗网络通过判别器判别真伪，最后希望生成网络生成数据能够以假乱真骗过判别器。

下面这张图表示生成对抗网络生成数据过程。

2.1 生成对抗网络模型概述

生成模型

在生成对抗网络中，不再是将图片输入编码器得到隐含向量然后生成图片，而是随机初始化一个隐含向量，根据变分自编码器的特点，初始化一个正态分布的隐含向量，通过类似解码的过程，将它映射到一个更高的维度，最后生成一个与输入数据相似的数据，这就是假的图片。生成对抗网络会通过对抗过程来计算出这个损失函数。

对抗模型

对抗模型简单来说就是一个判断真假的判别器，相当于一个二分类问题，真的图片输出1，假的图片输出0。对抗模型不关心图片的分类（例如，是猫还是狗），只关心图片的真假（不管是猫的图片还是狗的图片，对抗模型都会认为它是真的图片）。

生成对抗网络的训练

生成对抗网络在训练的时候，先训练判别器，将假的数据和真的数据都输入给判别模型，并优化这个判别器模型，希望它能够准确地判断出真的数据和假的数据。具体而言，是希望假数据尽可能得到标签0。

然后，开始训练生成器，希望它生成的假数据能够骗过已经经过优化的判别器。在这个阶段，将判别器的参数固定，通过反向传播优化生成器的参数，希望生成器得到的数据经过判别之后的标签尽可能是1（即为真数据）。

2.2 生成对抗网络的数学原理

这一节涉及到比较多的数学推理，但是对理解生成对抗网络很有帮助

推荐阅读：
生成对抗网络(GAN) 背后的数学理论

2.2.1 预备知识

KL散度

相对熵（relative entropy），又被称为Kullback-Leibler散度（Kullback-Leibler divergence）或信息散度（information divergence），是两个概率分布（probability distribution）间差异的非对称性度量。

KL散度是统计学中的一个概念，用于衡量两种概率分布的相似程度，数值越小，表示两种概率分布越接近。

假设$P(x)$和$Q(x)$是两个概率分布。若$P(x)$和$Q(x)$是离散的概率分布，则它们的KL散度定义为
$$D_{KL}(P||Q)=\sum _{i}P(i)\log \frac{P(i)}{Q(i)}$$

若$P(x)$和$Q(x)$是连续概率分布，则他们的KL散度定义为
$$D_{KL}(P||Q)={\int }_{-\infty }^{\infty }p(x)\log \frac{p(x)}{q(x)}dx$$

举个例子，假设有两个分布$A$和$B$，它们出现0和1的概率分别为
$$A(0)=\frac{1}{2},A(1)=\frac{1}{2},B(0)=\frac{1}{3},B(1)=\frac{2}{3}$$

那么，这两个概率分布的KL散度为
$$D_{KL}(P||Q)=\sum _{i}P(i)\log \frac{P(i)}{Q(i)}=A(0)\log \frac{A(0)}{B(0)}+A(1)\log \frac{A(1)}{B(1)}=\frac{1}{2}\log \frac{3}{2}+\frac{1}{2}\log \frac{3}{4}$$

极大似然估计

推荐阅读/参考文献：
一文搞懂极大似然估计
极大似然估计详解

极大似然估计，通俗理解来说，就是利用已知的样本结果信息，反推最具有可能（最大概率）导致这些样本结果出现的模型参数值！
换句话说，极大似然估计提供了一种给定观察数据来评估模型参数的方法，即：“模型已定，参数未知”。

我们先来看一下贝叶斯决策：
$$P(\omega |x)=\frac{P(x|\omega )P(\omega )}{P(x)}$$
其中$P(\omega )$为先验概率，即每种类别分布的概率；$P(x)$为某件事情发生的概率；$P(x|\omega )$为类条件概率，即某种类别前提下，某事发生的概率；$P(\omega |x)$为后验概率，即某事发生了，并且它属于某一类别的概率。后验概率越大，说明某事物属于这个类别的可能性越大，我们越有理由把它归到这个类别下。

实际问题中，我们可能只有样本数据，先验概率$P(\omega )$和类条件概率$P(x|\omega )$都是未知的。那么我们怎么根据仅有的样本数据进行分类呢？一种可行的办法就是对先验概率$P(\omega )$和类条件概率$P(x|\omega )$进行估计，然后再套用上述公式进行分类。

对先验概率$P(\omega )$的估计是比较简单的，我们可以利用经验或者依据数据样本中各类别出现的频率进行估计。

而对类条件概率$P(x|\omega )$的估计就难得多。原因包括：概率密度函数包含了一个随机变量的全部信息；样本数据可能不多；特征向量x的维度可能很大等等。一个解决的方法就是把概率密度$p(x|{\omega }_i)$的估计转化为参数估计问题（参数估计方法）。比如可以假设为正态分布，那么需要估计的参数就是$\sigma$和$\mu$。当然，概率密度分布$p(x|{\omega }_i)$非常重要。同时，采用这种参数估计的方法，要求数据满足“独立同分布”的假设，并且要保证样本量充足。

那么，假设我们已经确定了概率密度分布的模型，我们怎么确定哪些参数组合时最好的呢？这就是“极大似然估计”的目的。

最大似然估计的目的就是：利用已知的样本结果，反推最有可能（最大概率）导致这样结果的参数值。

原理：极大似然估计是建立在极大似然原理的基础上的一个统计方法，是概率论在统计学中的应用。极大似然估计提供了一种给定观察数据来评估模型参数的方法，即：“模型已定，参数未知”。通过若干次试验，观察其结果，利用试验结果得到某个参数值能够使样本出现的概率为最大，则称为极大似然估计。

假设已知的样本集为$D=\{x_1,x_2,...,x_n\}$，需要估计的参数向量为$\theta$，则相对于$\{x_1,x_2,...,x_n\}$的$\theta$的似然函数（likehood function）为其联合概率密度函数$P(D|\theta )$，可以理解为在参数为$\theta$的条件下$D=\{x_1,x_2,...,x_n\}$发生的概率（数据样本服从独立同分布）：
$$l(\theta )=P(D|\theta )=p(x_1,x_2,...,x_n|\theta )=\prod _{i=1}^{n}p(x_i|\theta )$$

这样一来，要使似然函数最大（即在参数为$\theta$的条件下$D=\{x_1,x_2,...,x_n\}$发生的概率最大），就是求似然函数$l(\theta )$的极值$\hat{\theta }$，$\hat{\theta }$称作极大似然函数估计值
$$\hat{\theta }=arg\underset{\theta }{\max }l(\theta )=arg\underset{\theta }{\max }\prod _{i=1}^{n}p(x_i|\theta )$$

为了便于分析，定义似然函数的对数
$$H(\theta )=\ln l(\theta )$$
$$\hat{\theta }=arg\underset{\theta }{\max }H(\theta )=arg\underset{\theta }{\max }\ln l(\theta )=arg\underset{\theta }{\max }\sum _{i=1}^N\ln p(x_i|\theta )$$

求极值自然就是求导了。

1. 如果$\theta$为标量，则在似然函数满足连续、可微的正则条件下，极大似然估计量是下面微分方程的解
   $$\frac{\mathrm{d}l(\theta )}{\mathrm{d}\theta }=0或者等价于\frac{\mathrm{d}H(\theta )}{\mathrm{d}\theta }=\frac{\mathrm{d}\ln l(\theta )}{\mathrm{d}\theta }=0$$

2. 如果未知参数有很多个，即$\theta$为向量，则可以对每个参数求偏导数，得到梯度算子
   $$\theta =[{\theta }_1,{\theta }_2,...,{\theta }_s{]}^T$$
   $${\nabla }_{\theta }=[\frac{\partial }{\partial {\theta }_1},\frac{\partial }{\partial {\theta }_2},...,\frac{\partial }{\partial {\theta }_s}]$$
   若似然函数满足连续可导的条件，则最大似然估计量就是如下方程的解。
   $${\nabla }_{\theta }H(\theta )={\nabla }_{\theta }\ln l(\theta )=\sum _{i=1}^N{\nabla }_{\theta }\ln P(x_i|\theta )=0$$

2.2.2 生成对抗网络的数学原理

我们再回到我们的生成对抗网络。

我们想要将一个随机高斯噪声$z$通过一个生成网络$G$得到一个和真实数据分布$P_{data}(x)$差不多的生成分布$P_G(x;\theta )$，其中参数$\theta$是 网络的参数，并且我们希望$\theta$可以使$P_G(x;\theta )$尽可能和$P_{data}(x)$接近。

我们从真实数据分布$P_{data}(x)$中取样$m$个点，$\{x^1,x^2,...x^m\}$。根据给定的参数$\theta$可以计算概率$P_G(x^i;\theta )$，那么生成$m$个样本数据的似然就是
$$L=\prod _{i=1}^m{P}_G(x^i;\theta )$$

则极大似然函数估计值$\hat{\theta }$为
$$\begin{array}{rl}\hat{\theta }& =arg\underset{\theta }{\max }\prod _{i=1}^m{P}_G(x^i;\theta )=arg\underset{\theta }{\max }\ln \prod _{i=1}^m{P}_G(x^i;\theta )=arg\underset{\theta }{\max }\sum _{i=1}^N\ln P_G(x_i|\theta )\\ & \approx arg\underset{\theta }{\max }{E}_{x\sim P_{data}}[\ln P_G(x;\theta )]\\ & \iff arg\underset{\theta }{\max }{\int }_x{P}_{data}(x)\ln P_G(x;\theta )\mathrm{d}x-{\int }_x{P}_{data}(x)\ln P_{data}(x;\theta )\mathrm{d}x\\ & =arg\underset{\theta }{\max }{\int }_x{P}_{data}(x)\ln \frac{P_G(x;\theta )}{P_{data}(x)}\mathrm{d}x\\ & =arg\underset{\theta }{\min }KL(P_{data}(x)||P_G(x;\theta ))\end{array}$$
也就是说，极大似然的另一个角度就是使KL散度极小。其中
$$P_G(x)={\int }_x{P}_{prior}(x)I_{[G(z)=x]}\mathrm{d}z$$
里面的$I$表示指示性函数，即
$$I_{G(z)=x}=\{\begin{array}{ll}0,& G(z)\ne x\\ 1,& G(z)=x\end{array}$$

也就是说，我们希望得到一组模型参数$\hat{\theta }$，使得其随机生成的向量的概率分布$P_G(x;\theta )$与真实向量的概率分布$P_{data}(x;\theta )$之间的KL散度最小（KL散度用于衡量两种概率分布的相似程度，数值越小，表示两种概率分布越接近）。

那么，我们怎么得到$P_G(x;\theta )$呢？在生成对抗网络中，生成器（生成模型，Generator，G）的作用就是将服从正态分布的样本得到输出集合，通过计算输出集合中各类样本的频次，会得到一个概率分布，这个概率分布就是$P_G(x;\theta )$。这里的$\theta$就是生成器的神经网络模型的参数。换句话说，机器学习的任务就是不断地训练、学习参数$\theta$，使得$P_G(x;\theta )$与$P_{data}(x;\theta )$之间的KL散度最小。而判别器（对抗模型，Discriminator，D）的作用就是衡量$P_G(x;\theta )$与$P_{data}(x;\theta )$之间的差距。

我们知道，判别器的作用其实是一个二分类问题，那么我们可以定义判别器的目标函数$V(G,D)$为
$$V(G,D)=E_{x\sim P_{data}}[\ln D(X)]+E_{x\sim P_G}[\ln (1-D(X))]$$
这个函数和逻辑回归的目标函数的形式是一样的。

我们的目标是找到一个合适的判别器$D$，使得${\max }_{D}V(G,D)$。为什么呢？因为我们希望判别器能够判断哪个是真，哪个是假，自然是他们之间的差距越大越好。由
$$\begin{array}{rl}V(G,D)& =E_{x\sim P_{data}}[\ln D(X)]+E_{x\sim P_G}[\ln (1-D(X))]\\ & ={\int }_x{P}_{data}(x)\ln D(x)\mathrm{d}x+{\int }_x{P}_G(x)\ln (1-D(x))\mathrm{d}x\\ & ={\int }_x[P_{data}(x)\ln D(X)+P_G(x)\ln (1-D(X))]\mathrm{d}x\end{array}$$

那么，
$$\begin{array}{rl}\underset{D}{\max }V(G,D)& =\underset{D}{\max }{\int }_x[P_{data}(x)\ln D(X)+P_G(x)\ln (1-D(X))]\mathrm{d}x\\ & \iff \underset{D}{\max }[P_{data}(x)\ln D(X)+P_G(x)\ln (1-D(X))]\end{array}$$

在给定生成器$G$的前提下，$P_{data}(x)$与$P_G(x)$都可以看成是常数，分别用$a$和$b$来表示，那么，等价于求解$f(D)$的极值，$f(D)$为
$$\begin{array}{r}f(D)=a\ln (D)+b\ln (1-D)\\ \frac{\mathrm{d}f(D)}{\mathrm{d}D}=a\times \frac{1}{D}+b\times \frac{1}{1-D}\times (-1)=0\\ \Rightarrow a\times \frac{1}{D^{\ast }}=b\times \frac{1}{1-D^{\ast }}\\ \Rightarrow a\times (1-D^{\ast })=b\times D^{\ast }\\ D^{\ast }(x)=\frac{a}{a+b}=\frac{P_{data}(x)}{P_{data}(x)+P_G(x)}\end{array}$$

这样就求得了在给定$G$的前提下，使得$V(D)$取得最大值的$D$。将$D$带回到$V(D)$，得到

$$\begin{array}{rl}\max V(G,D)& =V(G,D^{\ast })\\ & =E_{x\sim P_{data}}[\ln \frac{P_{data}(x)}{P_{data}(x)+P_G(x)}]+E_{x\sim P_G}[\ln \frac{P_G(x)}{P_{data}(x)+P_G(x)})]\\ & ={\int }_x{P}_{data}\log \frac{\frac{1}{2}{P}_{data}(x)}{\frac{P_{data}(x)+P_G(x)}{2}}\mathrm{d}x+{\int }_x{P}_G\log \frac{\frac{1}{2}{P}_G(x)}{\frac{P_{data}(x)+P_G(x)}{2}}\mathrm{d}x\\ & =-2\log 2+KL(P_{data}(x)||\frac{P_{data}(x)+P_G(x)}{2})+KL(P_G(x)||\frac{P_{data}(x)+P_G(x)}{2})\\ & =-2\log 2+2JSD(P_{data}(x)||P_G(x))\end{array}$$

其中$JSD(\ast )$为JS散度，定义为
$$JSD(P||Q)=\frac{1}{2}D(P||M)+\frac{1}{2}D(Q||M)M=\frac{1}{2}(P+Q)$$

这也就是为什么我们再训练生成对抗网络的时候，先训练判别器。因为我们首先希望得到判别器的参数${\theta }_D$，使其能够将真假图片最大化，以得到较优的判别器。

然后我们在这个较优判别器的基础上，再训练生成器，我们希望得到生成器的参数${\theta }_G$，能够和真实数据之间的概率分布的KL散度最小，即整体的优化目标是
$$G^{\ast }=arg\underset{G}{\min }\underset{D}{\max }V(G,D)$$

3 【案例一】利用PyTorch实现GAN【生成新的图片】

完整代码

在这个案例里面，我们同样是希望能够生成手写数字的图片。数据集是MNIST。

3.1 模型构建

构建判别器——对抗模型

判别器的结构非常简单，由三层全连接神经网络构成，中间使用了斜率为0.2的LeakyReLU激活函数。 leakyrelu 是指 f(x) = max($\alpha$ x, x)。

class discriminator(nn.Module):
    def __init__(self):
        super().__init__()
        self.net = nn.Sequential(nn.Linear(784, 256),
                                 nn.LeakyReLU(0.2),
                                 nn.Linear(256, 256),
                                 nn.LeakyReLU(0.2),
                                 nn.Linear(256, 1)
                                 )
    
    def forward(self, x):
        x = self.net(x)
        return x

构建生成器——生成模型

生成网络的结构也很简单，最后一层的激活函数选择tanh()函数的目的是将图片规范化到-1~1之间。

class generator(nn.Module):
    def __init__(self, input_size):
        super(generator, self).__init__()
        self.gen =nn.Sequential(
                nn.Linear(input_size, 1024),
                nn.ReLU(True),
                nn.Linear(1024, 1024),
                nn.ReLU(True),
                nn.Linear(1024, 784),
                nn.Tanh()
                )
    
    def forward(self, x):
        x = self.gen(x)
        return x

3.2 损失函数和优化器

bce_loss = nn.BCEWithLogitsLoss()

def discriminator_loss(logits_real, logits_fake): # 判别器的 loss
    size = logits_real.shape[0]
    true_labels = Variable(torch.ones(size, 1)).float().cuda()
    false_labels = Variable(torch.zeros(size, 1)).float().cuda()
    loss = bce_loss(logits_real, true_labels) + bce_loss(logits_fake, false_labels)
    return loss

def generator_loss(logits_fake): # 生成器的 loss  
    size = logits_fake.shape[0]
    true_labels = Variable(torch.ones(size, 1)).float().cuda()
    loss = bce_loss(logits_fake, true_labels)
    return loss

# 使用 adam 来进行训练，学习率是 3e-4, beta1 是 0.5, beta2 是 0.999
def get_optimizer(net):
    optimizer = torch.optim.Adam(net.parameters(), lr=3e-4, betas=(0.5, 0.999))
    return optimizer

3.3 训练模型

def train_a_gan(D_net, G_net, D_optimizer, G_optimizer, discriminator_loss, generator_loss, show_every=250, 
                noise_size=NOISE_DIM, num_epochs=10):
    iter_count = 0
    for epoch in range(num_epochs):
        for x, _ in train_data:
            bs = x.shape[0]
            # 判别网络
            real_data = Variable(x).view(bs, -1).cuda() # 真实数据
            logits_real = D_net(real_data) # 判别网络得分
            
            sample_noise = (torch.rand(bs, noise_size) - 0.5) / 0.5 # -1 ~ 1 的均匀分布
            g_fake_seed = Variable(sample_noise).cuda()
            fake_images = G_net(g_fake_seed) # 生成的假的数据
            logits_fake = D_net(fake_images) # 判别网络得分

            d_total_error = discriminator_loss(logits_real, logits_fake) # 判别器的 loss
            D_optimizer.zero_grad()
            d_total_error.backward()
            D_optimizer.step() # 优化判别网络
            
            # 生成网络
            g_fake_seed = Variable(sample_noise).cuda()
            fake_images = G_net(g_fake_seed) # 生成的假的数据

            gen_logits_fake = D_net(fake_images)
            g_error = generator_loss(gen_logits_fake) # 生成网络的 loss
            G_optimizer.zero_grad()
            g_error.backward()
            G_optimizer.step() # 优化生成网络

            if (iter_count % show_every == 0):
                print('Iter: {}, D: {:.4}, G:{:.4}'.format(iter_count, d_total_error.item(), g_error.item()))
                imgs_numpy = deprocess_img(fake_images.data.cpu().numpy())
                show_images(imgs_numpy[0:16])
                plt.show()
                print()
            iter_count += 1

训练结果如下：

可以看到，在iteration=4000的时候，隐约有了手写数字的样子。

3.4 采用不同的loss函数

Least Squares GAN
比最原始的 GANs 的 loss 更加稳定。我们可以定义一下loss函数：

def ls_discriminator_loss(scores_real, scores_fake):
    loss = 0.5 * ((scores_real - 1) ** 2).mean() + 0.5 * (scores_fake ** 2).mean()
    return loss

def ls_generator_loss(scores_fake):
    loss = 0.5 * ((scores_fake - 1) ** 2).mean()
    return loss

再次训练，可以比较一下采用不同的loss函数的结果：

3.5 使用更复杂的卷积神经网络

前面只是使用了简单的全连接网络来构建生成器和判别器，我们同样可以使用更复杂的卷积神经网络来构建生成器和判别器。

判别器

class build_dc_classifier(nn.Module):
    def __init__(self):
        super(build_dc_classifier, self).__init__()
        self.conv = nn.Sequential(
            nn.Conv2d(1, 32, 5, 1),
            nn.LeakyReLU(0.01),
            nn.MaxPool2d(2, 2),
            nn.Conv2d(32, 64, 5, 1),
            nn.LeakyReLU(0.01),
            nn.MaxPool2d(2, 2)
        )
        self.fc = nn.Sequential(
            nn.Linear(1024, 1024),
            nn.LeakyReLU(0.01),
            nn.Linear(1024, 1)
        )
        
    def forward(self, x):
        x = self.conv(x)
        x = x.view(x.shape[0], -1)
        x = self.fc(x)
        return x

生成器

class build_dc_generator(nn.Module): 
    def __init__(self, noise_dim=NOISE_DIM):
        super(build_dc_generator, self).__init__()
        self.fc = nn.Sequential(
            nn.Linear(noise_dim, 1024),
            nn.ReLU(True),
            nn.BatchNorm1d(1024),
            nn.Linear(1024, 7 * 7 * 128),
            nn.ReLU(True),
            nn.BatchNorm1d(7 * 7 * 128)
        )
        
        self.conv = nn.Sequential(
            nn.ConvTranspose2d(128, 64, 4, 2, padding=1),
            nn.ReLU(True),
            nn.BatchNorm2d(64),
            nn.ConvTranspose2d(64, 1, 4, 2, padding=1),
            nn.Tanh()
        )
        
    def forward(self, x):
        x = self.fc(x)
        x = x.view(x.shape[0], 128, 7, 7) # reshape 通道是 128，大小是 7x7
        x = self.conv(x)
        return x

开始训练

训练结果与简单全连接神经网络的对比如下：

可以看到，采用卷积神经网络训练的效果要好很多很多。

4. 【案例二】使用语言模型生成新的文本

上面一个案例主要是关于新图片的生成，而也有很多深度学习任务的数据集是和文本有关的。我们同样可以利用LSTM来创建新的文本序列。简单来说，我们希望模型能够根据给定的上下文预测下一个词。生成序列化数据这一能力在很多领域都有应用，比如图像标注、语音识别、语言翻译、自动回复邮件等等。

github：Word-level language modeling RNN