关联规则挖掘(Apriori算法和FP-Growth算法)
一、关联规则概述
1.关联规则分析用于在一个数据集中找出各种数据项之间的关联关系,广泛用于购物篮数据、个性化推荐、预警、时尚穿搭、生物信息学、医疗诊断、网页挖掘和科学数据分析中
2.关联规则分析又称购物篮分析,最早是为了发现超市销售数据库中不同商品之间的关联关系。
3.常用的关联规则分析算法

二、几个概念
1.项目:一个字段,比如一次交易订单中的一个商品
2.项集:包含若干个项目的集合,项目数量为k,则称为k项集
3.事务:一次交易中所有项目的集合
4.关联规则的表示形式:
(1)支持度:支持度为某项集在数据集中出现的频率。即项集在记录中出现的次数,除以数据集中所有记录的数量。
(2)置信度:关联规则{AB}中,置信度为A与B同时出现的次数,除以A出现的次数。
(3)提升度:关联规则{AB}中,提升度为{AB}的置信度,除以B的支持度。
5.频繁项集:满足最小支持度阈值与最小置信度阈值的项集称为频繁项集
(1)频繁项集具有强关联规则
6.闭项集:对于项集X来说,若数据集中不存在与项集X相同支持度的项集Y,那么项集X可称为闭项集X
7.频繁闭项集:对于频繁项集X来说,若数据集中不存在与频繁项集X相同支持度的频繁项集Y,那么频繁项集X可称为频繁闭项集X
8.极大项集:若项集X包含的项目数量最多,那么称项集X为极大项集。
9.极大频繁项集:若频繁项集X包含的项目数量最多,那么称项集X为极大频繁项集。
三、Apriori算法:通过限制候选产生发现频繁项集
1.定义
1994年,Rakesh Agrawal和Ramakrishnan Srikant 在Fast algorithms for mining association rules in large databases一文中正式提出Apriori算法用于挖掘数据库中频繁项集,是布尔关联规则挖掘频繁项集的原创性算法,通过限制候选集产生发现频繁项集。Apriori算法使用一种称为逐层搜索的迭代方法,其中k项集用于探索(k+1)项集。具体过程描述如下:首先扫描数据库,累计每个项的计数,并收集满足最小支持度的项找出频繁1项集记为L1,然后使用L1找出频繁2项集的集合L2,使用L2找出L3,迭代直到无法再找到频繁k项集为止,找出每个Lk需要一次完整的数据库扫描。
逐层搜索图例
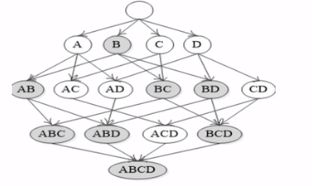
2.先验性质:
(1)如果项集L1不是频繁项集,那么项集L1的超项集L2也不可能是频繁项集
(2)如果项集L5是频繁项集,那么频繁项集L5的派生项集L4和L1一定是频繁项集
3.Apriori算法的步骤
(1)找出所有支持度大于等于最小支持度阈值的频繁项集。
(2)由频繁模式生成满足可信度阈值的关联规则。
4.连接+剪枝


(1)C:候选集
(2)L:频繁项集的集合
5.由频繁项集产生关联规则
(1)例子


置信区间与置信度的关系:当样本量给定时,置信区间的宽度随着置信水平的增大而增大;当置信水平固定时,置信区间的宽度随样本量的增大而减小,也就是说,较大的样本所提供的有关总体的信息要比较小的样本多。
置信度与精度的关系:当样本量给定时,误差范围随着置信度的增大而增大,即精度随置信度的增加而减小;当置信度固定时,误差范围随着样本量的增大而减小。因此,可通过增加样本量来提高精度。
给定的置信度在医学领域应该约高越好,理应在99%以上。
6.总结Apriori算法的一般过程
(1) 收集数据:使用任意方法。
(2) 准备数据:任何数据类型都可以,因为我们只保存集合。
(3) 分析数据:使用任意方法。
(4) 训练算法:使用Apriori算法来找到频繁项集。
(5) 测试算法:不需要测试过程。
(6) 使用算法:用于发现频繁项集以及物品之间的关联规则。
7.Apriori算法的优缺点
优点:易编码实现。
缺点:在大数据集上可能较慢。
适用数据类型:数值型或者标称型数据。
8.解决方法
(1)缩小产生的候选集
(2)改进对候选集支持度计算方法
四、FP-Growth算法:使用FP-growth算法来高效发现频繁项集
FP-growth算法只需要对数据库进行两次扫描,而Apriori算法对于每个潜在的频繁项集都会扫描数据集判定给定模式是否频繁,因此FP-growth算法的速度要比Apriori算法快。在小规模数据集上,这不是什么问题,但当处理更大数据集时,就会产生较大问题。FP-growth只会扫描数据集两次,它发现频繁项集的基本过程如下:
(1) 构建FP树
(2) 从FP树中挖掘频繁项集
1.定义:频繁模式增长(FP-growth)是一种基于Apriori的改进算法,优点是不产生候选频繁项集
2.算法原理:它采用分治策略(Divide and Conquer),在经过第一遍扫描之后,把代表频繁项集的数据库压缩进一棵频繁模式树(FP-tree),同时依然保留其中的关联信息,然后将FP-tree分化成一些条件库,每个库和一个长度为1的项集相关,再对这些条件库分别进行递归挖掘(降低了I/O开销)。
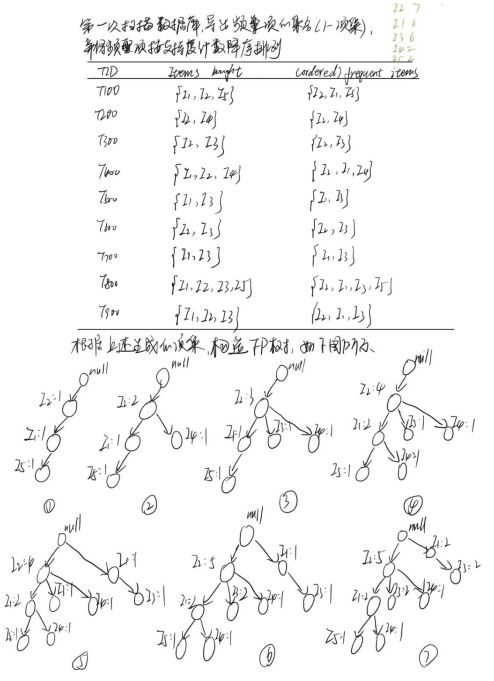
3.例子
(1)构造FP-tree
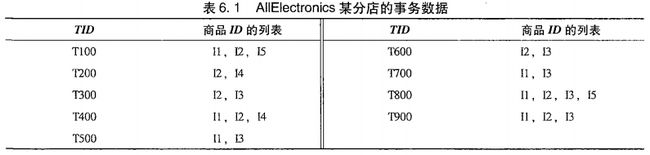
(2)创建项表头,使每个项目通过节点链指向它在树种的位置
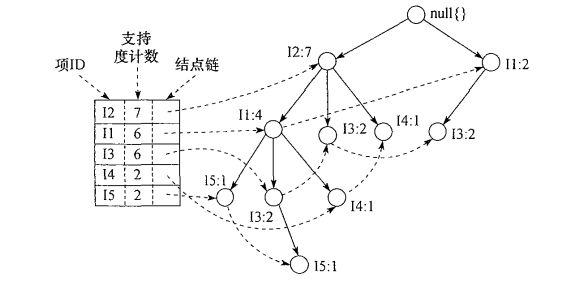
(3)FP-tree挖掘
I.从项头表开始挖掘,由频率低的结点开始
II.根据FP-tree得出各个项目(节点)的条件模式基(节点为叶子的生成子树)
例如:I5的条件模式基{I2,I1:1},{I2,I1,I3:1}
III.根据各个节点的条件模式基构造条件FP树(所有祖宗节点计数均变为叶子节点计数,再删除低于支持度的结点)
例如:结点I4的条件模式基{I2,I1:1},{I2:1},则结点I4的条件FP树如下图所示:
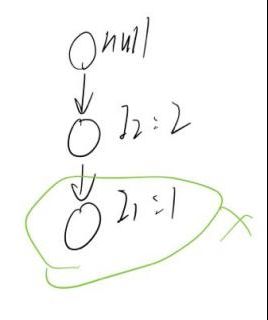
关于结点I4的频繁项集为{I2,I4}

FP- growth方法将发现长频繁模式的问题转换成在较小的条件数据库中递归地搜索一些较短模式,然后连接后缀。它使用最不频繁的项作后缀,提供了较好的选择性。该方法显著地降低了搜索开销。
对FP-groith方法的性能研究表明:对于挖掘长的频繁模式和短的频繁模式,它都是有效的和可伸缩的,并且大约比Apriori 算法快一个数量级。
4.FP-growth算法优缺点
优点:一般要快于Apriori。
缺点:实现比较困难,在某些数据集上性能会下降。
适用数据类型:标称型数据。
5.总结FP-growth的一般流程
(1) 收集数据:使用任意方法。
(2) 准备数据:由于存储的是集合,所以需要离散数据。如果要处理连续数据,需要将它们量化为离散值。
(3) 分析数据:使用任意方法。
(4) 训练算法:构建一个FP树,并对树进行挖据。
(5) 测试算法:没有测试过程。
(6) 使用算法:可用于识别经常出现的元素项,从而用于制定决策、推荐元素或进行预测等应用中。
五、基于Python实现Apriori算法
Python代码如下:
#-*- coding: utf-8 -*-
import os
import time
#python进度条库
from tqdm import tqdm
begin_time =time.time()
def load_data(path):#根据路径加载数据集
ans=[]#将数据保存到该数组
if path.split(".")[-1]==("xls" or "xlsx"):#若路径为药方.xls
from xlrd import open_workbook
# import xlwt
workbook=open_workbook(path)
sheet=workbook.sheet_by_index(0)#读取第一个sheet
for i in range(1,sheet.nrows):#忽视header,从第二行开始读数据,第一列为处方ID,第二列为药品清单
temp=sheet.row_values(i)[1].split(";")[:-1]#取该行数据的第二列并以“;”分割为数组
if len(temp)==0: continue
temp=[j.split(":")[0] for j in temp]#将药品后跟着的药品用量去掉
temp=list(set(temp))#去重,排序
temp.sort()
ans.append(temp)#将处理好的数据添加到数组
elif path.split(".")[-1]=="csv":
import csv
with open(path,"r") as f:
reader=csv.reader(f)
for row in reader:
row=list(set(row))#去重,排序
row.sort()
ans.append(row)#将添加好的数据添加到数组
return ans#返回处理好的数据集,为二维数组
def save_rule(rule,path):#保存结果到txt文件
with open(path,"w") as f:
f.write("index confidence"+" rules\n")
index=1
for item in rule:
s=" {:<4d} {:.3f} {}=>{}\n".format(index,item[2],str(list(item[0])),str(list(item[1])))
index+=1
f.write(s)
f.close()
print("result saved,path is:{}".format(path))
class Apriori():
def create_c1(self,dataset):#遍历整个数据集生成c1候选集
c1=set()
for i in dataset:
for j in i:
item = frozenset([j])
c1.add(item)
return c1
def create_ck(self,Lk_1,size):#通过频繁项集Lk-1创建ck候选项集
Ck = set()
l = len(Lk_1)
lk_list = list(Lk_1)
for i in range(l):
for j in range(i+1, l):#两次遍历Lk-1,找出前n-1个元素相同的项
l1 = list(lk_list[i])
l2 = list(lk_list[j])
l1.sort()
l2.sort()
if l1[0:size-2] == l2[0:size-2]:#只有最后一项不同时,生成下一候选项
Ck_item = lk_list[i] | lk_list[j]
if self.has_infrequent_subset(Ck_item, Lk_1):#检查该候选项的子集是否都在Lk-1中
Ck.add(Ck_item)
return Ck
def has_infrequent_subset(self,Ck_item, Lk_1):#检查候选项Ck_item的子集是否都在Lk-1中
for item in Ck_item:
sub_Ck = Ck_item - frozenset([item])
if sub_Ck not in Lk_1:
return False
return True
def generate_lk_by_ck(self,data_set,ck,min_support,support_data):#通过候选项ck生成lk,并将各频繁项的支持度保存到support_data字典中
item_count={}#用于标记各候选项在数据集出现的次数
Lk = set()
for t in tqdm(data_set):#遍历数据集
for item in ck:#检查候选集ck中的每一项是否出现在事务t中
if item.issubset(t):
if item not in item_count:
item_count[item] = 1
else:
item_count[item] += 1
t_num = float(len(data_set))
for item in item_count:#将满足支持度的候选项添加到频繁项集中
if item_count[item] >= min_support:
Lk.add(item)
support_data[item] = item_count[item]
return Lk
def generate_L(self,data_set, min_support):#用于生成所有频繁项集的主函数,k为最大频繁项的大小
support_data = {} #用于保存各频繁项的支持度
C1 = self.create_c1(data_set) #生成C1
L1 = self.generate_lk_by_ck(data_set, C1, min_support, support_data)#根据C1生成L1
Lksub1 = L1.copy() #初始时Lk-1=L1
L = []
L.append(Lksub1)
i=2
while(True):
Ci = self.create_ck(Lksub1, i) #根据Lk-1生成Ck
Li = self.generate_lk_by_ck(data_set, Ci, min_support, support_data) #根据Ck生成Lk
if len(Li)==0:break
Lksub1 = Li.copy() #下次迭代时Lk-1=Lk
L.append(Lksub1)
i+=1
for i in range(len(L)):
print("frequent item {}:{}".format(i+1,len(L[i])))
return L, support_data
def generate_R(self,dataset, min_support, min_conf):
L,support_data=self.generate_L(dataset,min_support)#根据频繁项集和支持度生成关联规则
rule_list = []#保存满足置信度的规则
sub_set_list = []#该数组保存检查过的频繁项
for i in range(0, len(L)):
for freq_set in L[i]:#遍历Lk
for sub_set in sub_set_list:#sub_set_list中保存的是L1到Lk-1
if sub_set.issubset(freq_set):#检查sub_set是否是freq_set的子集
#检查置信度是否满足要求,是则添加到规则
conf = support_data[freq_set] / support_data[freq_set - sub_set]
big_rule = (freq_set - sub_set, sub_set, conf)
if conf >= min_conf and big_rule not in rule_list:
rule_list.append(big_rule)
sub_set_list.append(freq_set)
rule_list = sorted(rule_list,key=lambda x:(x[2]),reverse=True)
return rule_list
if __name__=="__main__":
##config
filename="groceries.csv"
min_support=25#最小支持度
min_conf=0.7#最小置信度
#获取当前路径
current_path=os.getcwd()
#若找不到次路径,添加log文件
if not os.path.exists(current_path+"/log"):
os.mkdir("log")
#数据集存放路径
path=current_path+"/dataset/"+filename
#结果存放路径
save_path=current_path+"/log/"+filename.split(".")[0]+"_apriori.txt"
#加载数据
data=load_data(path)
print(data)
# #调用写好的Apriori类
apriori=Apriori()
rule_list=apriori.generate_R(data,min_support=15,min_conf=0.7)
save_rule(rule_list,save_path)
end_time = time.time()
run_time = end_time-begin_time
print ('该循环程序运行时间:{:.2f}s'.format(run_time)) #该循环程序运行时间:
六、基于Python实现FP-Growth算法
Python代码如下:
#-*- coding: utf-8 -*-
import os
import time
from tqdm import tqdm
begin_time =time.time()
#第一次扫描数据集
def load_data(path):#根据路径加载数据集
ans=[]#将数据保存到该数组
if path.split(".")[-1]==("xls" or "xlsx"):#若路径为药方.xls
from xlrd import open_workbook
import xlwt
workbook=open_workbook(path)
sheet=workbook.sheet_by_index(0)#读取第一个sheet
for i in range(1,sheet.nrows):#忽视header,从第二行开始读数据,第一列为处方ID,第二列为药品清单
temp=sheet.row_values(i)[1].split(";")[:-1]#取该行数据的第二列并以“;”分割为数组
if len(temp)==0: continue
temp=[j.split(":")[0] for j in temp]#将药品后跟着的药品用量去掉
temp=list(set(temp))#去重,排序
temp.sort()
ans.append(temp)#将处理好的数据添加到数组
elif path.split(".")[-1]=="csv":
import csv
with open(path,"r") as f:
reader=csv.reader(f)
for row in reader:
row=list(set(row))#去重,排序
row.sort()
ans.append(row)#将添加好的数据添加到数组
return ans#返回处理好的数据集,为二维数组
def save_rule(rule,path):#保存结果到txt文件
with open(path,"w") as f:
f.write("index confidence"+" rules\n")
index=1
for item in rule:
s=" {:<4d} {:.3f} {}=>{}\n".format(index,item[2],str(list(item[0])),str(list(item[1])))
index+=1
f.write(s)
f.close()
print("result saved,path is:{}".format(path))
class Node:
def __init__(self, node_name,count,parentNode):
self.name = node_name
self.count = count
self.nodeLink = None#根据nideLink可以找到整棵树中所有nodename一样的节点
self.parent = parentNode#父亲节点
self.children = {}#子节点{节点名字:节点地址}
class Fp_growth():
#更新头结点
def update_header(self,node, targetNode):#更新headertable中的node节点形成的链表
while node.nodeLink != None:
node = node.nodeLink
node.nodeLink = targetNode
#更新树的分支
def update_fptree(self,items, node, headerTable):#用于更新fptree
if items[0] in node.children:
# 判断items的第一个结点是否已作为子结点
node.children[items[0]].count+=1
else:
# 创建新的分支
node.children[items[0]] = Node(items[0],1,node)
# 更新相应频繁项集的链表,往后添加
if headerTable[items[0]][1] == None:
headerTable[items[0]][1] = node.children[items[0]]
else:
self.update_header(headerTable[items[0]][1], node.children[items[0]])
# 递归
if len(items) > 1:
self.update_fptree(items[1:], node.children[items[0]], headerTable)
#创建树
def create_fptree(self,data_set, min_support,flag=False):#建树主函数
'''
根据data_set创建fp树
header_table结构为
{"nodename":[num,node],..} 根据node.nodelink可以找到整个树中的所有nodename
'''
item_count = {}#统计各项出现次数
for t in data_set:#第一次遍历,得到频繁一项集
for item in t:
if item not in item_count:
item_count[item]=1
else:
item_count[item]+=1
headerTable={}
for k in item_count:#剔除不满足最小支持度的项
if item_count[k] >= min_support:
headerTable[k]=item_count[k]
freqItemSet = set(headerTable.keys())#满足最小支持度的频繁项集
if len(freqItemSet) == 0:
return None, None
for k in headerTable:
headerTable[k] = [headerTable[k], None] # element: [count, node]
tree_header = Node('head node',1,None)
if flag:
ite=tqdm(data_set)
else:
ite=data_set
for t in ite:#第二次遍历,建树
localD = {}
for item in t:
if item in freqItemSet: # 过滤,只取该样本中满足最小支持度的频繁项
localD[item] = headerTable[item][0] # element : count
if len(localD) > 0:
# 根据全局频数从大到小对单样本排序
order_item = [v[0] for v in sorted(localD.items(), key=lambda x:x[1], reverse=True)]
# 用过滤且排序后的样本更新树
self.update_fptree(order_item, tree_header, headerTable)
return tree_header, headerTable
def find_path(self,node, nodepath):
'''
递归将node的父节点添加到路径
'''
if node.parent != None:
nodepath.append(node.parent.name)
self.find_path(node.parent, nodepath)
#找出条件模式基
def find_cond_pattern_base(self,node_name, headerTable):
'''
根据节点名字,找出所有条件模式基
'''
treeNode = headerTable[node_name][1]
cond_pat_base = {}#保存所有条件模式基
while treeNode != None:
nodepath = []
self.find_path(treeNode, nodepath)
if len(nodepath) > 1:
cond_pat_base[frozenset(nodepath[:-1])] = treeNode.count
treeNode = treeNode.nodeLink
return cond_pat_base
#条件树
def create_cond_fptree(self,headerTable, min_support, temp, freq_items,support_data):
# 最开始的频繁项集是headerTable中的各元素
freqs = [v[0] for v in sorted(headerTable.items(), key=lambda p:p[1][0])] # 根据频繁项的总频次排序
for freq in freqs: # 对每个频繁项
freq_set = temp.copy()
freq_set.add(freq)
freq_items.add(frozenset(freq_set))
if frozenset(freq_set) not in support_data:#检查该频繁项是否在support_data中
support_data[frozenset(freq_set)]=headerTable[freq][0]
else:
support_data[frozenset(freq_set)]+=headerTable[freq][0]
cond_pat_base = self.find_cond_pattern_base(freq, headerTable)#寻找到所有条件模式基
cond_pat_dataset=[]#将条件模式基字典转化为数组
for item in cond_pat_base:
item_temp=list(item)
item_temp.sort()
for i in range(cond_pat_base[item]):
cond_pat_dataset.append(item_temp)
#创建条件模式树
cond_tree, cur_headtable = self.create_fptree(cond_pat_dataset, min_support)
if cur_headtable != None:
self.create_cond_fptree(cur_headtable, min_support, freq_set, freq_items,support_data) # 递归挖掘条件FP树
#根据条件树,挖掘频繁项
def generate_L(self,data_set,min_support):
freqItemSet=set()
support_data={}
tree_header,headerTable=self.create_fptree(data_set,min_support,flag=True)#创建数据集的fptree
#创建各频繁一项的fptree,并挖掘频繁项并保存支持度计数
self.create_cond_fptree(headerTable, min_support, set(), freqItemSet,support_data)
max_l=0
for i in freqItemSet:#将频繁项根据大小保存到指定的容器L中
if len(i)>max_l:max_l=len(i)
L=[set() for _ in range(max_l)]
for i in freqItemSet:
L[len(i)-1].add(i)
for i in range(len(L)):
print("frequent item {}:{}".format(i+1,len(L[i])))
return L,support_data
#挖掘关联规则
def generate_R(self,data_set, min_support, min_conf):
L,support_data=self.generate_L(data_set,min_support)
rule_list = []
sub_set_list = []
for i in range(0, len(L)):
for freq_set in L[i]:
for sub_set in sub_set_list:
if sub_set.issubset(freq_set) and freq_set-sub_set in support_data:#and freq_set-sub_set in support_data
conf = support_data[freq_set] / support_data[freq_set - sub_set]
big_rule = (freq_set - sub_set, sub_set, conf)
if conf >= min_conf and big_rule not in rule_list:
# print freq_set-sub_set, " => ", sub_set, "conf: ", conf
rule_list.append(big_rule)
sub_set_list.append(freq_set)
rule_list = sorted(rule_list,key=lambda x:(x[2]),reverse=True)
return rule_list
if __name__=="__main__":
#config
filename="groceries.csv"
min_support=25#最小支持度
min_conf=0.7#最小置信度
spend_time=[]
current_path=os.getcwd()
if not os.path.exists(current_path+"/log"):
os.mkdir("log")
path=current_path+"/dataset/"+filename
save_path=current_path+"/log/"+filename.split(".")[0]+"_fpgrowth.txt"
#加载数据集
data_set=load_data(path)
# print(data_set)
#调用Fp_growth算法
fp=Fp_growth()
#生成关联规则
rule_list = fp.generate_R(data_set, min_support, min_conf)
#保存文件
save_rule(rule_list,save_path)
end_time = time.time()
run_time = end_time-begin_time
print ('该循环程序运行时间:{:.2f}s'.format(run_time)) #该循环程序运行时间:
七、结论与建议
(一)结果分析
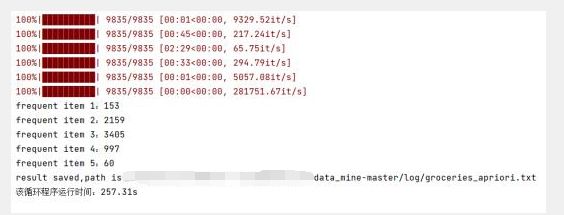
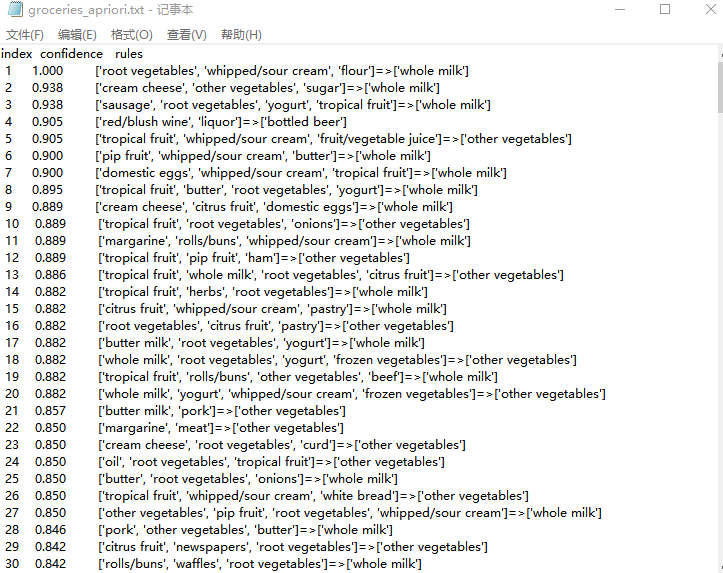
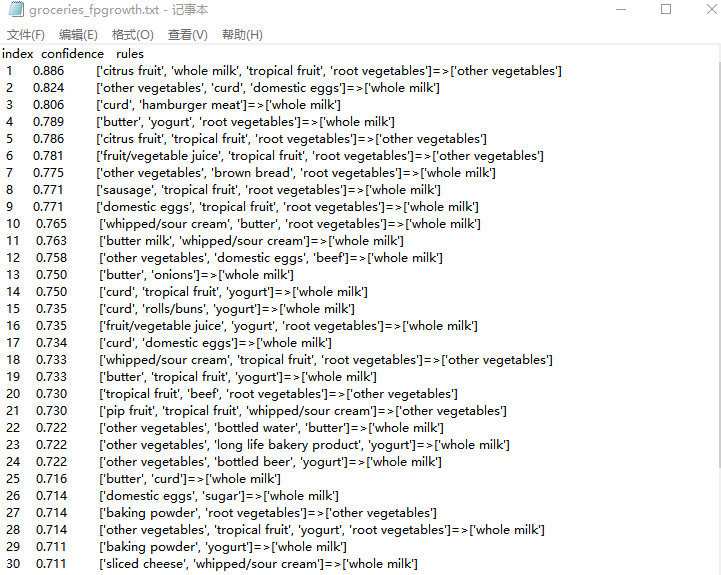
本例探究了顾客在杂货店购买商品时是否存在关联规则的情况,基于groceries.csv数据集,并将最小支持度设置为25,最小置信度设置为0.7。使用Apriori算法进行关联规则分析,输出了300条关联规则,其中当客户购买[‘root vegetables’, ‘whipped/sour cream’, ‘flour’]这三种商品时购买[‘whole milk’]的置信度是1;使用FP-growth算法进行关联规则分析,输出了36条关联规则,其中当客户购买[‘citrus fruit’, ‘whole milk’, ‘tropical fruit’, ‘root vegetables’]这三种商品时购买[‘other vegetables’]的置信度是0.886 ;店家可以根据分析情况摆放商品,将置信度高的商品摆放一起可以增加客户的购买力。
(二)结果比较

由图可知,FP-growth算法比Apriori算法快一个数量级,在空间复杂度方面也比Apriori也有数量级级别的优化。
我们发现Apriori算法的频繁项集的方式是:先产生低阶频繁项集(从1开始的)的,再由低阶频繁项集产生高阶候选项集,高阶候选项集经过支持度的度量筛选产生,最后生成同阶频繁项集。这是不断重复的“产生-测试”的过程。而FP-growth算法采用是完全不同的方式,算法的第一个核心是压缩数据集,采用的是FP_tree这样的一个数据结构来完全表示了所有的事务,第二个核心是采用了“分而治之”的思想,用递归的方式将挖掘频繁项集一步步分成各自的子问题来解决。对比于Apriori算法,FP-growth算法的特点是只需要扫描两次数据集和无需产生候选项集。
关联规则挖掘是个值得深入研究的研究。本文通过对经典算法的研究,实现对经典算法的初步实现。但是还有许多值得深入研究的地方:
(1)数据挖掘的基本问题在于数据的处理,数据结构的优化和挖掘算法效率的提高,是今后不断需要努力的地方。
(2)采用多层关联规则和多维关联规则分析技术挖掘更多的潜在信息。