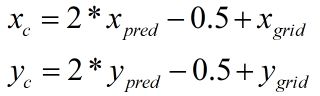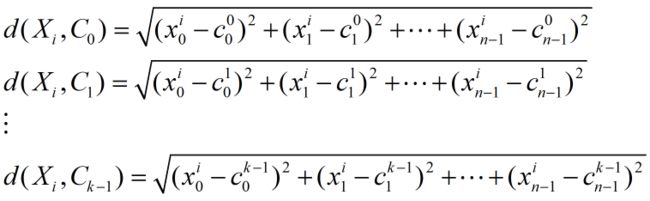基于libtorch的yolov5目标检测网络实现(3)——Kmeans聚类获取anchor框尺寸
算上这一篇,yolov5目标检测框架我们已经更新到第3篇了,前面两篇分别讲解了coco数据集json标签文件的解析,以及yolov5网络的网络结构与实现:
基于libtorch的yolov5目标检测网络实现——COCO数据集json标签文件解析
基于libtorch的yolov5目标检测网络实现(2)——网络结构实现
在本文中,我们主要讲目标检测中anchor框的概念以及使用kmeans聚类算法获取anchor框尺寸的原理与实现。
01
上篇文章所讲的CSP1_n和CSP2_n结构有误,在此做出纠正
上篇文章中,我们讲到CSP1_n和CSP2_n的结构中都包含了若干个ResUnit_n模块,其中每个ResUnit_n模块又包含了若干个CBL模块,如下图所示:
ResUnit_n结构
CSP1_n和CSP2_n的错误结构
其实上图的CSP1_n和CSP2_n结构是不对的,实际上每个CSP1_n或CSP2_n仅包含一个ResUnit_n模块,而不是多个。其中n值决定了ResUnit_n模块中CBL模块的个数,也即输入的n值确定了CSP1_n和CSP2_n中CBL模块的个数为2n。如下图所示:
CSP1_n和CSP2_n的正确结构
02
预测目标框回归原理
当我们初次看到“预测目标框回归”这个字眼的时候,往往是懵逼的,其实它也没有那么玄乎,这就是一个把网络的预测信息转换为实际目标框信息的操作。那么问题来了,为什么需要一个转换操作呢?
假如让网络直接去预测目标框的位置坐标和宽高,坐标与宽高的取值范围都太广泛了,这无疑增大了网络的训练时间和学习难度,导致网络的不稳定,严重情况下甚至使网络在错误的学习方向上渐行渐远。
为解决该问题,yolov5网络在预测信息中加入了目标框的先验信息。通俗理解,就是在网络训练之前,人为地先告诉网络目标框的信息范围,比如框中心坐标的取值范围、宽高的取值范围。然后网络在这个取值范围的基础上再去学习,以获得更精确的框信息。这样一来相当于对网络的学习方向作了限制,因此很大程度增加了网络的稳定性以及收敛速度。如下图所示:
具体做法:
-
框的中心坐标
我们在前文已经讲过,yolov5网络把640*640的图像划分成N*N(通常为80*80,或40*40,或20*20)的网格区域。网络的输出端则输出所有网格的预测信息,每个网格的预测信息包括目标的分类概率、置信度,以及目标框的x中心坐标、y中心坐标、长、宽(xpred、ypred、wpred、hpred)。对于每个网格,它预测目标框的位置就在该网格附近,因此x中心坐标、y中心坐标的大概范围是可以确定的,利用此特性可以对该网格预测的x中心坐标、y中心坐标作取值范围限制,如下式:
上式中,xgrid和ygrid为该网格的网格坐标(0≤xgrid
-
框的宽、高
预测目标框的宽、高也加入了先验信息:
上式中,wpred和hpred为网络输出的目标框宽、高预测值(0
那么wanchor和hanchor又是怎么事先得到的呢?这就需要对训练集包含的所有目标框的宽、高做统计分析了——统计训练集中所有目标框的宽、高,并从中提取出几个主要的宽、高组合,也即最具有代表性的宽、高组合,这几个宽高组合对应的几个方框,就是我们所说的anchor框。yolov5网络使用kmeans算法将训练集所包含所有目标框的宽、高进行聚类,得到9个最具有代表性的宽、高组合,也即9个anchor框,然后根据宽、高的大小把这9个anchor分成3组:
-
宽、高最小的3个anchor框分配给80*80网格的每一个格子
-
宽、高居中的3个anchor框分配给40*40网格的每一个格子
-
宽、高最大的3个anchor框分配给20*20网格的每一个格子
这与前文我们说的每一层网格输出信息就对应了起来,以下3*80*80、3*40*40、3*20*20中的数字3也即对应上方的3个anchor框:
-
80*80网格输出3*80*80个小尺寸检测目标的信息
-
40*40网格输出3*40*40个中尺寸检测目标的信息
-
20*20网格输出3*20*20个大尺寸检测目标的信息
03
Kmeans算法原理
跟我们前文讲过的DBSCAN聚类算法、AGNES聚类算法类似,kmeans也是一种常用的无监督聚类算法。
DBSCAN聚类算法的理解与应用
AGNES聚类算法的理解与应用
假设数据集有X0、X 1、X 2、…、X m-1这m个样本,其中每个样本Xi又是一个长度为n的一维向量:
那么Kmeans算法的基本步骤如下:
-
从m个样本中随机选择k个样本(C0、C 1、C 2、…、C k-1)作为中心点,这里的k为预先设定好的类别数,比如yolov5需要根据宽、高把训练集的所有目标框分成9类,那么k=9。
-
分别计算每个样本与k个中心点的距离,然后将该样本分配给距其最近的中心点。距离的度量通常使用欧式距离,比如对于任意样本Xi,分别计算其与C0、C 1、C 2、…、C k-1的欧式距离(如下式),然后比较d(Xi,C0)、d(Xi,C1)、d(Xi,C2)、…、d(Xi,Ck-1)得出距离样本Xi最小的中心点,并将样本Xi分配给该中心点。
-
经过步骤2,每个样本都被分配给距离它最近的1个中心点,分配到相同中心点的所有样本组成1个类别或簇,因此所有样本被分成了k个簇。然后计算k个簇的质心,作为新的k个中心点把原本中心点取代掉。比如某个簇包含3个样本Xt0、X t1、X t2,那么该簇的质心C i按下式计算:
-
判断步骤3得到的新中心点相对原中心点的的变化量是否小于设定阈值,小于阈值则停止计算。再判断2、3步骤的重复次数(迭代次数)是否超过设定次数,如果超过也停止计算。
04
Opencv3.4.1的Kmeans算法接口说明
Opencv3.4.1集成了Kmeans算法:
double kmeans(
InputArray data,
int K,
InputOutputArray bestLabels,
TermCriteria criteria,
int attempts,
int flags,
OutputArray centers = noArray()
);
参数说明:
| data | cv::Mat类型,为输入的数据样本,每行为一个样本,因此行数等于样本总数,列数等于每个样本的数据长度,仅支持float类型数据 |
| K | 聚类划分的类别数 |
| bestLabels | cv::Mat类型,输出的样本标签,行数等于样本总数,列数为1,每行的值表示其对应的样本被划分到哪个类别中 |
| criteria | TermCriteria类型,输入的算法终止条件,可以是超过指定迭代次数时终止,也可以是到达指定迭代精度时终止,或者两者兼顾 |
| attempts | Kmeans算法的计算次数,不同次计算得到的聚类结果可能时不一样的,选择最好的结果输出 |
| flags | 获取初始中心点的方法,支持:KMEANS_RANDOM_CENTERS、KMEANS_PP_CENTERS、KMEANS_USE_INITIAL_LABELS这三种方法,最常用的为KMEANS_RANDOM_CENTERS随机选取方法 |
| centers_ | cv:Mat类型,输出最终的中心点,行数为K,列数为每个样本的数据长度 |
测试代码:
void kmeans_test(void)
{
//10个待聚类样本,每个样本的数据长度为1
float buffer[10] = {0.1, 5.2, 10.35, 0.08, 4.9, 5.234, 11.0, 0.12, 9.89, 0.05};
Mat input(10, 1, CV_32FC1, buffer);
const int K = 3; //划分为3类
const int attemps = 300; //kmeans计算300次
//迭代终止条件
const cv::TermCriteria term_criteria = cv::TermCriteria(cv::TermCriteria::EPS + cv::TermCriteria::COUNT, 300, 0.01);
cv::Mat labels_, centers_;
cv::kmeans(input, K, labels_, term_criteria, attemps, cv::KMEANS_RANDOM_CENTERS, centers_);
cout << input << endl;
cout << endl << labels_ << endl;
cout << endl << centers_ << endl;
}
运行结果:
05
Kmeans聚类获取anchor框
yolov5使用Kmeans算法聚类训练集中所有目标框的宽、高,结果得到9个宽、高组合,也即得到9个anchor框。不过这里使用Kmeans算法的样本距离度量不是欧式距离,而是iou距离,因为yolo系列的作者认为当不同样本的宽、高差距比较大时,使用欧式距离会导致聚类结果误差很大,所以改为使用iou距离。下面我们介绍一下iou的概念。
iou是衡量两个方框相似度(包括位置、宽、高的相似度)的量,是两个方框相交区域面积与相并部分面积的比值,所以也称为交并比。
如上图所示,两个方框的宽、高分别为(w1,h1)和(w2,h2),红色区域为两个框的相交区域,其宽、高为(w,h),“蓝+红+灰”区域为两个框的相并区域,那么相交区域的面积为:
相并区域的面积为:
那么得到iou:
iou的取值范围为[0,1],当两个框没有相交区域时iou取0,当两个框完全重合时iou取1。所以iou值越大说明两个框的形状和位置越相似。为了使度量值与相似度负相关,也即度量值越小相似度越大,我们对iou值取个负值并加1,得到:
上式就是使用Kmeans算法聚类目标框宽、高时使用的距离度量。因为我们只关心框的宽、高,不关心它们的位置,所以假设两个框的中心点是重合的,如下图所示:
不过,如果我们使用Opencv的Kmeans算法来计算,存在一个问题,就是Opencv的Kmeans算法默认使用欧式距离衡量样本距离,不能使用iou度量,所以会存在上述说的不同样本宽、高差距大导致聚类结果误差大的问题。为了使用Opencv的Kmeans接口,又避免该问题,我们可以先对每个目标框的宽、高做一个归一化,使它们的值都在0~1范围之间,这样就不存在数值差别大的问题了。如下式,其中row、col分别为图像的高和宽:
最后聚类得到的结果,也是0~1之间的值,所以我们需要再乘以640,转换为640*640坐标系的宽、高。代码如下,其中json标签文件的解析,我们前文已经讲过:
void kmeans_antror(void)
{
json j;
//解析json标签文件,得到训练集包含的所有目标框的宽、高
ifstream jfile("D:/数据/coco/annotations_trainval2017/annotations/instances_train2017.json");
jfile >> j;
ns::coco_label cr;
ns::from_json(j, cr);
//每个样本的数据内容为宽、高,因此每个样本的数据长度为2
Mat input = Mat::zeros(cr.annotations_list.size(), 2, CV_32FC1);
for (int i = 0; i < cr.annotations_list.size(); i++)
{
cout << "i: " << i << endl;
//读取目标框对应的图像,得到图像的宽、高
Mat image = read_img_grom_id("F:/train2017/%012d.jpg", cr.annotations_list[i].image_id);
//对目标框的宽、高做归一化
float w = cr.annotations_list[i].bbox[2] / image.cols;// *640;
float h = cr.annotations_list[i].bbox[3] / image.rows;// *640;
//将目标框的宽、高写入Opencv的Mat中
input.ptr(i)[0] = w;
input.ptr(i)[1] = h;
}
const int K = 9; //聚类的类别数
const int attemps = 300; //kmeans算法的计算次数
//迭代的停止条件
const cv::TermCriteria term_criteria = cv::TermCriteria(cv::TermCriteria::EPS + cv::TermCriteria::COUNT, 300, 0.01);
cv::Mat labels_, centers_;
cv::kmeans(input, K, labels_, term_criteria, attemps, cv::KMEANS_RANDOM_CENTERS, centers_);
//将聚类得到的0~1结果乘以640转换得到640*640图像中的对应目标框宽、高
cout << centers_ * 640 << endl;
}
运行结果如下,从上到下就是9个anchor框的宽、高:
欢迎扫码关注本微信公众号,接下来会不定时更新更加精彩的内容,敬请期待~