梯度下降法——一元线性回归（实战）

import numpy as np
import matplotlib.pyplot as plt

# 载入数据
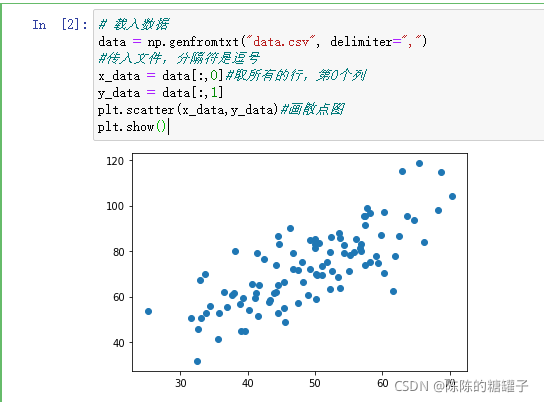
data = np.genfromtxt("data.csv", delimiter=",")
#传入文件，分隔符是逗号
x_data = data[:,0]#取所有的行，第0个列
y_data = data[:,1]
plt.scatter(x_data,y_data)#画散点图
plt.show()

# 学习率learning rate
lr = 0.0001
# 截距
b = 0 
# 斜率
k = 0 
# 最大迭代次数
epochs = 50

# 最小二乘法
def compute_error(b, k, x_data, y_data):
    totalError = 0
    for i in range(0, len(x_data)):
        totalError += (y_data[i] - (k * x_data[i] + b)) ** 2
        #真实值减去预测值，然后平方，累加
    return totalError / float(len(x_data)) / 2.0 
    #然后累加值除与样本个数*2

    
def gradient_descent_runner(x_data, y_data, b, k, lr, epochs):
    # 计算总数据量
    m = float(len(x_data))
    # 循环epochs次
    for i in range(epochs):
        b_grad = 0
        k_grad = 0
        # 计算梯度的总和再求平均
        for j in range(0, len(x_data)):
            #相当于对斜率和截距求导后循环将每个x值代入
            b_grad += (1/m) * (((k * x_data[j]) + b) - y_data[j])
            k_grad += (1/m) * x_data[j] * (((k * x_data[j]) + b) - y_data[j])
        # 更新b和k
        b = b - (lr * b_grad)
        k = k - (lr * k_grad)
        # 每迭代5次，输出一次图像
#        if i % 5==0:
#            print("epochs:",i)
#            plt.plot(x_data, y_data, 'b.')
 #           plt.plot(x_data, k*x_data + b, 'r')
#            plt.show()
    return b, k

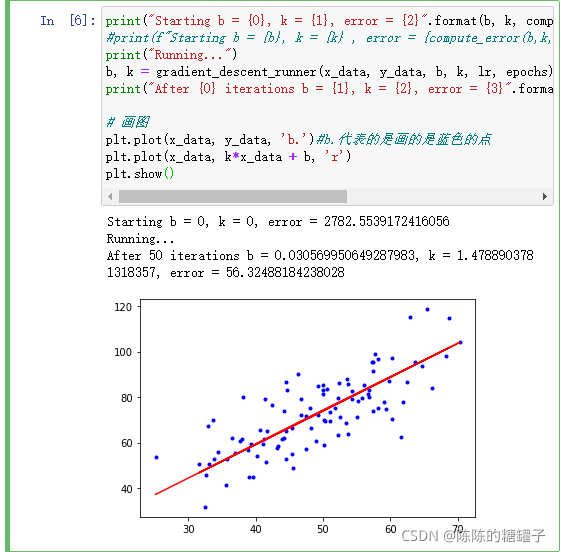
print("Starting b = {0}, k = {1}, error = {2}".format(b, k, compute_error(b, k, x_data, y_data)))
#print(f"Starting b = {b}, k = {k} , error = {compute_error(b,k,x_data,y_data)}" )
print("Running...")
b, k = gradient_descent_runner(x_data, y_data, b, k, lr, epochs)
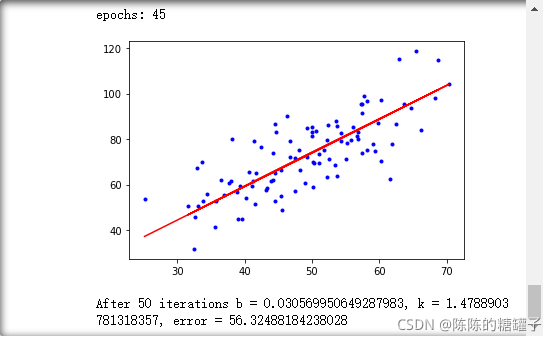
print("After {0} iterations b = {1}, k = {2}, error = {3}".format(epochs, b, k, compute_error(b, k, x_data, y_data)))

# 画图
plt.plot(x_data, y_data, 'b.')#b.代表的是画的是蓝色的点
plt.plot(x_data, k*x_data + b, 'r')
plt.show()

或者你想要更好地观察过程，可以让它每五次画图一次

# 学习率learning rate
lr = 0.0001
# 截距
b = 0 
# 斜率
k = 0 
# 最大迭代次数
epochs = 50

# 最小二乘法
def compute_error(b, k, x_data, y_data):
    totalError = 0
    for i in range(0, len(x_data)):
        totalError += (y_data[i] - (k * x_data[i] + b)) ** 2
        #真实值减去预测值，然后平方，累加
    return totalError / float(len(x_data)) / 2.0 
    #然后累加值除与样本个数*2

    
def gradient_descent_runner(x_data, y_data, b, k, lr, epochs):
    # 计算总数据量
    m = float(len(x_data))
    # 循环epochs次
    for i in range(epochs):
        b_grad = 0
        k_grad = 0
        # 计算梯度的总和再求平均
        for j in range(0, len(x_data)):
            #相当于对斜率和截距求导后循环将每个x值代入
            b_grad += (1/m) * (((k * x_data[j]) + b) - y_data[j])
            k_grad += (1/m) * x_data[j] * (((k * x_data[j]) + b) - y_data[j])
        # 更新b和k
        b = b - (lr * b_grad)
        k = k - (lr * k_grad)
        # 每迭代5次，输出一次图像
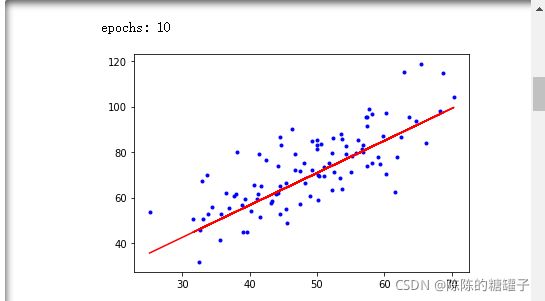
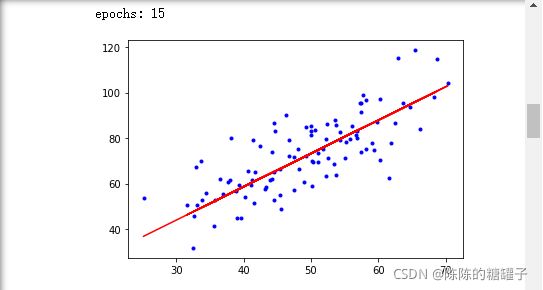
        if i % 5==0:
            print("epochs:",i)
            plt.plot(x_data, y_data, 'b.')
            plt.plot(x_data, k*x_data + b, 'r')
            plt.show()
    return b, k

print("Starting b = {0}, k = {1}, error = {2}".format(b, k, compute_error(b, k, x_data, y_data)))
#print(f"Starting b = {b}, k = {k} , error = {compute_error(b,k,x_data,y_data)}" )
print("Running...")
b, k = gradient_descent_runner(x_data, y_data, b, k, lr, epochs)
print("After {0} iterations b = {1}, k = {2}, error = {3}".format(epochs, b, k, compute_error(b, k, x_data, y_data)))

# 画图
# plt.plot(x_data, y_data, 'b.')#b.代表的是画的是蓝色的点
# plt.plot(x_data, k*x_data + b, 'r')
# plt.show()