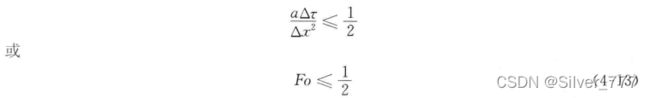用Matlab求解一维非稳态导热问题（有限差分法+显式离散）

章熙民的第六版《传热学》里，较为简单的介绍了非稳态导热的数值计算，本文根据此书，以计算一个可视为无限大平壁的复合墙体传热过程为例，讨论一维非稳态导热问题数值求解的问题。

这里把参考书目的PDF分享出来，希望可以帮助到大家学习传热学，里面有章熙民的第六版《传热学》和陶文铨的第二版《数值传热学》。

链接：https://pan.baidu.com/s/1vQFmnWrVXH-SKTTbPJhzZg 
提取码：bxgr 

一、问题描述与分析

初始条件：一个由四层材料构成的墙体（可视为无限大平壁），已知材料热工性质如下，该墙体的内表面换热系数为8.7W/(m^2*K)，外表面换热系数为23W/(m^2*K)，室内温度为20℃恒定不变，室外温度随昼夜变化。

现给出一星期的室外温度数据（每小时），求墙体内部温度场。

构造层	材料	干密度ρ-kg/m^3	导热系数λ-W/(m*K)	比热容c- J/(Kg*K)	厚度mm	热扩散率a=λ/(c*ρ) m^2/s
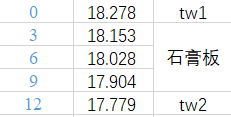
1	石膏板	1050	0.36	1050	12	3.2653E-07
2	钢筋混凝土	2500	2.04	920	120	8.8696E-07
3	聚苯乙烯泡沫板	20	0.046	1380	120	1.6667E-06
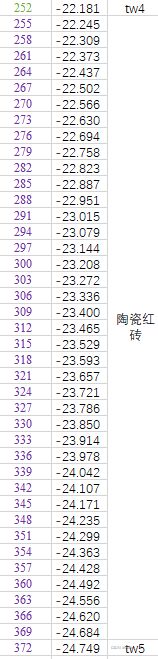
4	陶瓷红砖	1800	0.7	880	120	4.4192E-07

室外温度	第1天	第2天	第3天	第4天	第5天	第6天	第7天
0	-25.4	-24.5	-20.5	-19.8	-21	-23.5	-15.5
1	-25.4	-24.7	-21.3	-19.8	-23.1	-23.9	-15.9
2	-25.4	-25	-22	-19.8	-25.1	-24.4	-16.4
3	-25.4	-25.2	-22.9	-19.6	-24.4	-24.2	-17.5
4	-25.4	-25.5	-23.8	-19.4	-23.6	-24	-18.6
5	-25.4	-25.7	-24.7	-19.2	-22.9	-23.8	-19.7
6	-25.4	-26.4	-25.1	-19.2	-23.4	-23.2	-18
7	-25	-26.4	-25	-19	-23.5	-22.4	-15.6
8	-24	-25.4	-24.2	-18.5	-22.9	-21	-13.2
9	-22	-22.2	-22.3	-17.2	-20.4	-18.6	-11.6
10	-19.8	-18.9	-20.2	-15.7	-17.6	-15.8	-10.3
11	-17.8	-16.2	-18.2	-14.2	-14.9	-13.2	-9.2
12	-16.5	-15.6	-16.9	-13	-13.3	-11.2	-8.1
13	-15.8	-15.7	-16.2	-12.3	-12.7	-9.9	-7.4
14	-15.9	-16.3	-16.2	-12	-12.8	-9.5	-7.2
15	-17	-16.9	-17.1	-12.5	-14	-10.5	-7.7
16	-18.4	-17.7	-18.3	-13.3	-15.2	-12.1	-8.6
17	-20	-18.6	-19.4	-14.3	-16.2	-13.7	-9.9
18	-21.3	-19.4	-19.8	-15	-16.2	-13.9	-11.5
19	-22	-19.3	-19.7	-15.8	-16.8	-14.1	-13.4
20	-23	-19.6	-19.8	-16.5	-17.1	-14.4	-15.1
21	-23.4	-19.7	-19.8	-17.3	-19.1	-14.6	-15.8
22	-23.8	-19.7	-19.8	-18.2	-21	-14.8	-16.4
23	-24.2	-19.8	-19.8	-19	-23	-15	-17.1

问题分析

在《传热学》第四章第三节中，对什么是非稳态导热的给出了如下解释：

因此根据上述场景将该问题提炼为：一个两边是第三类边界条件的无限大平壁的一维非稳态导热问题。

二、节点方程式

在这里用的是有限差分法，节点方程式离散格式用的是显示离散格式（求解上更为简单，但是对步长要求较为严苛），数值求解过程参考章熙民《传热学》的第四章第三节。

内部节点方程式：

稳定条件：

边界节点方程式（第三类边界条件）：

 稳定条件：

网格划分

在经过多次试验之后，将该墙体按间距3mm划分为132层，取时间步长为1s，此时满足稳定条件。由于这里是复合墙体，因此后续计算时也要注意节点的热物性参数会相应改变。

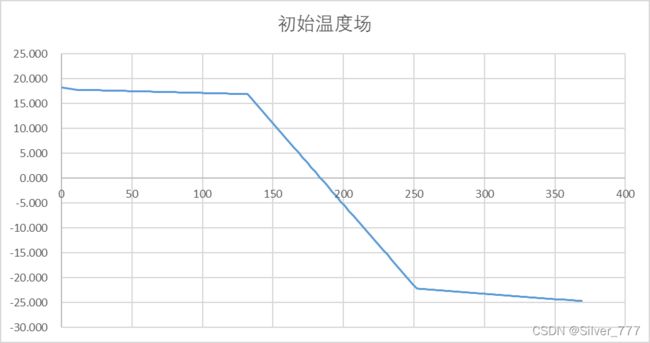
初始温度场设置

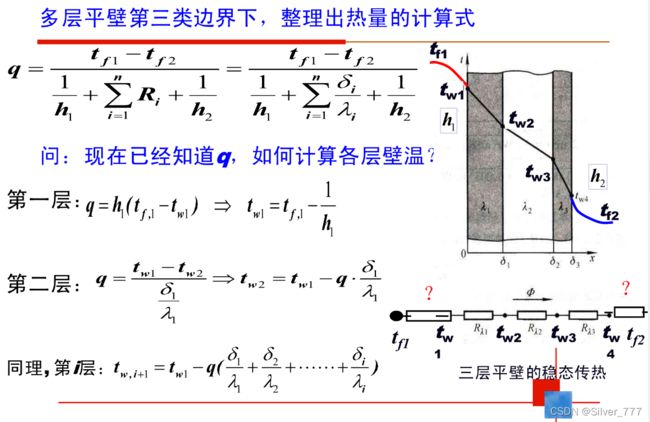
还有一个问题是墙体的初始温度场，显式离散格式的逻辑就是从初始温度出发逐个计算出各个时刻的温度。这里没有给，所以就用初始温度条件（室内20℃，室外-25.4℃）计算这一条件下的稳态温度。（注，其实根据周期性导热的规律，只要模拟的时间足够长，初始条件是什么并不重要，到最后墙体内部温度场都会是一个从外到内的、具有衰减性延时性的周期性温度波，这里将它的初始温度设置成这样是为了缩短模拟时长，让图像更好看）。复合平壁的稳态导热问题求解可以参考章熙民《传热学》的第二章第二节。

 根据上式求得墙体内初始温度场。

三、在Matlab中求解

在完成上述工作之后，便可以在Matlab中求解了。（注意室外温度outdoor_air和初始温度场wall都是自定义数组，运行本代码前需要在matlab里自己添加并定义这两个变量，我这里使用的值都在前面列出来了）。

clc;
clf;
format short e;
global N delta_x delta_t TN;

h1 = 8.7; %墙体内表面传热系数 W/(m^2*K)
h4 = 23; %墙体外表面传热系数 W/(m^2*K)
D = 0.332; %墙体厚度/m
N = 124; %厚度划分数目
delta_x = 0.003; %划分间距/m
delta_t = 1; %时间步长/s
day = 7; %计算天数
TN = 3600*24*day; %计算时间节点数目
Tn = 20; %室内温度
T = zeros(TN,N+1); %预设数组大小
Tf = zeros(1,TN);

%设置室外空气温度 这一步是因为给的是每小时的温度 换成每秒均等增加的温度值
for hour = 1:24*day %取值范围
    %将第hour小时和hour+1小时的温度等间距分成3600个
    %自定义数组outdoor_air为室外温度
    temp = linspace(outdoor_air(hour),outdoor_air(hour+1),3600); 
    for t = 1:3600
        Tf(3600*(hour-1)+t) = temp(t);%每秒均匀变化的温度
    end
end

%设置初始墙体内温度
for I = 1:N+1
    %自定义数组wall为墙体初始温度
    T(1,I) = wall(I);
end

%第一层：石膏板
a1 = 3.265e-7; %热扩散率 m^2/s
lamb1 = 0.36; %热导率 W/(m*K)
Fo1 = a1*delta_t/(delta_x)^2;
Bi1 = h1*delta_x/lamb1;
c1 = Fo1 - 1/(2*Bi1+2);

%第二层：钢筋混凝土
a2 = 8.870e-7; %热扩散率 m^2/s
lamb2 = 2.04; %热导率 W/(m*K)
Fo2 = a2*delta_t/(delta_x)^2;

%第三层：聚苯乙烯泡沫板
a3 = 1.667e-6; %热扩散率 m^2/s
lamb3 = 0.046; %热导率 W/(m*K)
Fo3 = a3*delta_t/(delta_x)^2;

%第四层：陶瓷红砖
a4 = 4.419e-7; %热扩散率 m^2/s
lamb4 = 0.7; %热导率 W/(m*K)
Fo4 = a4*delta_t/(delta_x)^2;
Bi4 = h4*delta_x/lamb4;
c4 = Fo4 - 1/(2*Bi4+2);

while (Fo1>0.5 || Fo2>0.5 || Fo3>0.5 || Fo4>0.5 || c4>0  || c1>0)
    error('无法收敛');
end

 上述代码为第一部分，主要是定义参数，设置初始条件，判断选择的步长是否满足稳定性条件。

for t = 1:TN
    for i = 1:N+1      
        if i == 1
            T(t+1,i) = 2*Fo1*(T(t,i+1) + Bi1*Tn) + (1 - 2*Bi1*Fo1 - 2*Fo1)*T(t,i);
        end
        
        if (i>=2 && i<= 5)
            T(t+1,i) =  Fo1*(T(t,i-1) + T(t,i+1)) + (1 - 2*Fo1)*T(t,i);
        end
        
        if (i>=6 && i<= 45)
            T(t+1,i) =  Fo2*(T(t,i-1) + T(t,i+1)) + (1 - 2*Fo2)*T(t,i);
        end
        
        if (i>=46 && i<= 85)
            T(t+1,i) =  Fo3*(T(t,i-1) + T(t,i+1)) + (1 - 2*Fo3)*T(t,i);
        end
        
        if (i>=86 && i<= 124)
            T(t+1,i) =  Fo4*(T(t,i-1) + T(t,i+1)) + (1 - 2*Fo4)*T(t,i);
        end
        
        if i == N+1
            T(t+1,i) = 2*Fo4*(T(t,i-1) + Bi4*Tf(t)) + (1 - 2*Bi4*Fo4 - 2*Fo4)*T(t,i);
            %这里给了室外空气温度Tf一个时间函数关系
        end
    end
end

上述为第二部分，就是计算显式离散节点方程了，没有什么好说的，就用了最简单的迭代法，甚至不需要求解方程组，唯一需要注意的就是由于是复合平壁，各个材料层的节点方程式使用的参数不一样。

X = zeros(1,24*day*2);
Y = zeros(1,N+1);
TT = zeros(24*day*2,N+1);

J = 1;
for I = 1:24*day*2
    X(I) = 1800*I; %30分钟一个数
    for J = 1:N+1
        Y(J) = J;
        TT(I,J) = T(X(I),Y(J));
    end
end
 
figure(1)
hold on;
 
% Make a contour with the presence of isolines & texts
[XX,YY] = meshgrid(Y,X);
surfc(YY,XX,TT)

xlabel('Time - AXIS')
ylabel('Thickness - AXIS')
zlabel('T (^{\circ}C)')
title(colorbar,'^{\circ}C')

上述代码为第三部分，画图，半个小时取一个数，因为一秒钟一个温度数太多了没有必要，图形会变黑。

最后呈现出来的温度-时间-节点的图形就是这样：

以上为本人对这个问题的数值求解，可能还有不正确的地方，欢迎指点。