【北邮果园大三上】数据挖掘

---

---

数据挖掘

大数据

定义：

• 体积
• 时效性
• 种类
• 值

数据挖掘模型

1.归纳已知

2.预测未来

1. 数据的质量处理和度量方法

1.1数据

1.1.1数据属性

属性类型:

• 标称(nominal)
• 序数(ordinal)
• 区间(interval)
• 比率(ratio)

非对称的属性(asymmetric attribute):

对于非对称的属性,非零值才是重要的

1.1.2数据类型

一般特征:

• 维度:指数据集中的对象具有的属性数目

• 疏松性:一个对象的大部分属性值都是0

• 分辨率:在不同分辨率下可以获得不同的数据

数据集合的类型

记录Record

• 关系记录

• 数据矩阵

• 交易数据

• 文档数据：文档文本：词频向量

图and网络

• 万维网

• 社会或信息网络

• 分子结构Molecular Structures

有序的Ordered

• 视频数据：sequence of images

• 时间数据：时间序列time-series

特殊的时序数据，其中每个记录都是一个时间序列（time series），即一段时间的测量序列

时间自相关（temporal autocorrelation），即如果两个测量的时间很接近，这些测量的值通常非常相似

序列数据：交易序列transaction sequences

• 记录数据的扩充
• 时间次序重要，但具体时间不重要
• 例：事务序列

遗传序列数据

• DNA都由4种核苷酸A、T、G、C构造
• 没有时间标记，但与时序数据类似
• 重要的是在序列中的位置

空间，图像image and 多媒体multimedia：

• Spatial data:maps
• Image data
• Video data

---

1.2 数据质量（重要）

主要着重于两个方面:

• 数据质量问题的检测和纠正
• 使用可以容忍低质量数据的算法

1.2.1测量和数据收集问题

• 噪声（重要）

指数据的无关值，噪声可能是离群点但也有可能是无关值

• 离群点（Outlier）：

在某种意义上不同于数据集中其他大部分数据对象特征的数据对象。我们也称之为异常值（anomalous），

离群点不是错误数据，并且需要 进行分析

• 精度、偏倚和准确率

精度（precision）：重复测量之间的接近程度

偏倚（bias）：测量值与被测量之间的系统的变差

准确度（accuracy）：被测量与测量值之间的接近度

• 数据缺失

  • 丢失原因

    • 数据未收集

    • 属性不一定适用于所有情况

  • 如何处理

    • 直接删除丢失数据

    • 估计数据或者变量

    • 估计丢失属性

      • 找到相似度最高的数据点
      • 连续属性
        • 使用最近的邻居的平均属性值
      • 离散
        • 那么可以采用最常出现的属性值

    • 忽视在检测中缺失的属性

• 数据重复

• 与应用相关的问题

  • 时效性
  • 相关性
    • 样本偏移（抽取样本与实际有差异）
    • 现有数据必须包含 应用所需的信息

1.3数据预处理

1.3.1聚集Aggregation

• 定义：将多个属性进行合并，变成一个属性

• 目的

  • 减少数据
  • 改变规模（从小变大）
  • 更加稳定的数据

1.3.2采样Sampling

• 目的：通过采样的方法减少计算个数

• 方式

  • 简单随机采样

    • 随机采样后 放回
    • 随机采样后 不放回
    • 分层采样（将数据分成几个分区;然后从每个分区中随机抽取样本）

  • 渐进采样法

    从小的样本开始构建，直到大到模型稳定为止

1.3.3维度减少

curse of dimensionality：当维度增加时，数据在它所占据的空间中变得越来越稀疏，使得数据的规律性变差失去原本意义

• 目的：

  • 避免维度灾难（curse of dimensionality）
  • 数据更加容易可视化
  • 减少数据挖掘算法所需的时间和内存
  • 有助于消除不相关到特征

• 技术

  • 主成分分析法（PCA）：使用处理方法进行属性合成（将高维映射到低维空间）

  • 有监督和非线性技术

1.3.4特征子集选择

另一个方法减少数据维度

• 去除冗长的属性
• 去除不相关的属性
• 归类方式的优化

1.3.5特征创建

• 定义：创建新的属性，可以比原始属性更有效地捕捉数据集中的重要信息。

• 技术

  • 特征抽取（从图像中提取边缘）
  • 特征创建（用质量除以体积得到密度）
  • 映射到新的空间（傅里叶和小波分析）

1.3.6分散化和二进制化

• 分散化

  • 定义：将连续属性转换为序数属性的过程，大量的值被映射到少量的类别中
  • 常用于分类中

• 二进制化

  • 定义：将一个连续的或分类的属性映射成一个或多个二进制变量

  **眼睛颜色 **和 身高 测量为{低、中、高}

1.3.7变量的变换

• 定义：通过计算，将不具有正态分布的属性变为具有正态分布的属性

  • 标准化：

    • 指各种技术，以调整属性之间在出现频率、平均值、方差、范围方面的差异
    • 剔除不需要的、常见的信号

  • 使用简单函数：
    $$x^k,log(x),e^x,|x|$$

1.3.8相似度和不相似度特征

• 相似度
  • 取值是0-1 越大越像
• 不相似度
  • 越小越像
  • 最小值为0

1.4欧式距离（Euclidean 重点）

• 一个标准化概念（比较的是两者的相似性）：
• 公式：

n是属性个数，x和y分别是同一属性，两个不同的 变量

$$d(x,y)=\sqrt{\sum _1^n(x_k-y_k{)}^2}$$

一般形式：（欧氏距离是r=2时的）

• 性质

  • 对于所有的x和y，d(x, y)>0，只有当x=y时，d(x, y)=0
  • 对于所有的x和y，d(x, y) = d(y, x) (对称性)
  • d(x, z) < d(x, y) + d(y, z) 对于所有的x、y和z点。 (三角形不等式)

1.4.1相似度（Similarity）

• 性质

  • 只有当x=y时，s(x, y)=1（或最大相似性）
  • s(x, y) = s(y, x) 对于所有x和y

• 术语：

  假设：对象p和q只有二进制属性

  f01 = p是0，q是1的属性的数量
  f10 = p为1，q为0的属性数量
  f00 = p为0，q为0的属性数
  f11 = p为1，q为1的属性数

简单匹配系数（SMC）：匹配的数量/属性的数量
$$SMC=(f_{11}+f_{00})/(f_{01}+f_{10}+f_{11}+f_{00})$$
（Jaccard）：上述公式去除0的项
$$Jaccard=(f_{11})/(f_{01}+f_{10}+f_{11})$$
例：

1.4.2余弦相似度

如果x和y是两个文件向量，那么

$$cos(x,y)=<x,y>/||x||\ast ||y||$$

其中表示向量x和y的内积或向量点积，||x||是向量x的长度。

例子：

1.4.3 相关性（Correlation）

• 相关性衡量对象

• 相关性可视化

  

• 应用领域

  • 记录数据、蛋白质、图像、序列等

例：

答案

2. 分类的基本方法

2.1 分类（Classification）

2.1.1定义

• 给出一个记录集合（训练集）

  • 每个记录的特征是一个元组（x,y）。

  其中x是属性集，y是类别

  

• 任务：将x映射到y上去（学习出一个方程建立xy到联系）

举例

Training训练集：用于建立模型

test测试集：用于测试建立的模型

2.2决策树

不需要从头开始生成一个决策树，重点在应用、对比性能、评价

决策树有多种建立方式

1.以家庭为根节点

2.以是否结婚为根节点

进行测试

• 决策树算法

  • Hunt’s Algorithm (one of the earliest)

  • ID3

  • CART（the extension of ID3）

  • C4.5（the extension of ID3）

  • SPRINT

  • SLIQ（the extension of C4.5）

2.2.1 Hunt’s Algorithm (one of the earliest)

• 定义：将一个样本进行决策树分类，分到一个分支只有一个分类为止

2.2.2属性测试条件

• 依赖于属性类型

  • 二进制

  • 名称属性

  • 有序的

  • 连续的

• 取决于分配方式的数量

  以名称属性进行分类

  • 双向拆分
  
  • 多项拆分

• 判断分类

不纯度要尽量低

2.2.3 衡量不纯度（重点）

i是出现次数，t是总共次数

图像

例：计算

• 加权基尼系数

当一个父亲结点分成了k个子节点

ni:第i个子节点数目

n：父亲结点总共个数

• 信息增益

对比前后基尼系数加权后的差值，越大越决策树简洁

例

上述方法可能导致模型复杂度过高，占用大量空间，下面就是评估模型复杂度的方式

• 增益率（GainRATIO）

根据不纯度和划分类别，评估模型

例

先计算划分类别系数

再进行增益率计算

…
第三个选项为最优

总结

优点

• 构建的成本很低
• 在对未知记录进⾏分类时速度极快
• 对⼩规模的树容易解释
• 对噪声具有鲁棒性（特别是当采⽤了避免过度拟合的⽅法时）。
• 可以很容易地处理冗余或不相关的属性（除⾮这些属性是相互影响的）。

缺点

• 可能的决策树的空间是指数级的⼤。Greedy（贪婪）⽅法往往不能找到最好的树。NP-hard。
• 不考虑属性之间的相互作⽤
• 每个决策边界只涉及⼀个属性

---

2.3 模型过度拟合

2.3.1 术语

• 训练误差

  在训练时产⽣的错误（不能正确归纳模型）

• 泛化误差

  对于未知样本不能正确推理

2.3.2 决策树构建

当节点少时，决策树准确率上升迅速

随着节点增多准确率逐渐上升（但不能过多）

2.3.3 过度拟合

随着训练的增多，训练误差减⼩（蓝⾊线），但是泛化误差增加（红⾊线）

拟合过多后，对于未知样本的推理能⼒下降

如果过拟合使得模型过于复杂，则应该对模型进行剪枝操作

2.3.4 产⽣过度拟合的原因

1. 噪声

由于两个样本错误产⽣了错误的训练模型

2. 学习样本太少

只有五个样本，没有与未知样本相似的模型

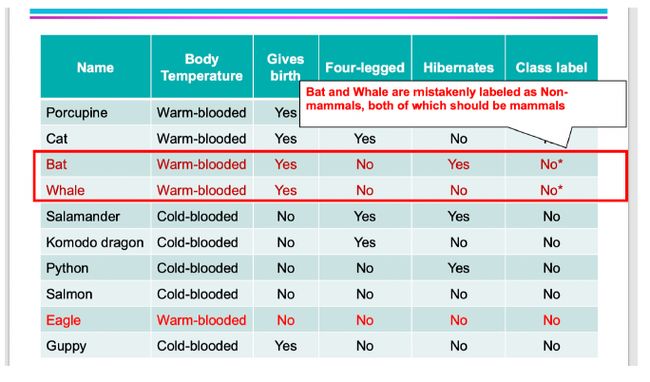
下图训练出的模型对 人类 进行分析会误判：（非哺乳类）

3. 多重⽐较过程（模型的复杂度较⾼）

存在⼀个⼩概率事件被⽤于模型拟合过程，产⽣过度拟合，导致泛化问题

考试连续猜对8道以上选择题概率很低：

但是该数据被用于拟合，属于小概率事件，会导致过拟合问题

---

2.4 模型评估

2.4.1 再代⼊估计-乐观估计（⽤训练误差代替泛化误差）

训练集准确度更高，所以使用训练误差代替泛化误差

例：

计算精准度

但不能光考虑准确性，还要考虑模型复杂度

2.4.2 结合模型复杂度

结合模型复杂性和分类模型评估的两种⽅法

• 悲观估计

相当于在乐观估计的分子上+Ω(T)（惩罚项）

$$\Omega (T)=\Omega \ast k$$

例：

• 最⼩描述⻓度（MDL）

找到模型长度和特例样本数最小

计算公式：

变量题⽬中会定义

模型编码长度+分类错误数据的编码长度

例：（P125 9）

解

2.4.3 统计上界（不考）

泛化误差也可以⽤训练误差的统计修正来估计。

由于泛化误差往往大于训练误差，统计修正通常是计算训练误差的上限，考虑到到达决策树的特定叶节点的训练记录的数量。

• 计算公式

2.4.4 使用确认集

我们将训练数据分为以下两种

• 训练集
  • ⽤于模型建⽴
• 确认集
  • ⽤于估计泛化误差

缺点：会导致训练集的样本数减少

2.5 处理过度拟合

2.5.1 先剪枝

• 在成为⼀棵完全生成模型之前设置终止条件，停⽌算法
• 条件
  • 样本属性值相同时终⽌
  • 如果所有的实例都属于同⼀类
  • 如果实例的数量少于⽤户指定的阈值，则停⽌。
  • 当样本和分类相互独⽴，则停⽌

2.5.2 后剪枝

在模型生成完后，进⾏调整与观察，去掉不好的分支

• 方法

  • -⼦树替换

    –如果修剪后泛化错误得到改善，⽤叶⼦节点替换⼦树

    –叶⼦节点的类别标签是由⼦树中⼤多数实例的类别决定的

  • ⼦树提⾼

    –⽤最常⽤的分⽀替换⼦树

---

2.6 模型对⽐

• 保持法Holdout（不放回）

  预留k%⽤于训练，(100-k)%⽤于测试

  • 限制因素：由于要保留⼀部分记录⽤于测试，因此⽤于训练的标记样本较少

• 随机抽样法Random subsampling: repeated holdout（不放回）

  多次重复保持法

  • 局限性：

    随机抽样法将遇到与保持法相同的问题

    由于⽆法控制每条记录⽤于训练和测试的次数，⼀些记录可能⽐其他记录更频繁地⽤于训练

• 交叉验证法Cross validation

  将数据划分为k个不相交的子集

  -k折（交叉验证）：在k-1个分区上训练，对剩下一个分区进行测试

  -重复k次，使得每份数据都用于检验恰好一次

  • 局限性：

    计算开销大，性能估计度量的方差偏高

• ⾃助法（Bootstrap）

  有放回进⾏采样，使数据等可能地被重新抽取（抽样过程重复b次，产生b个自助样本。）

  没有抽中的记录就成为检验集的一部分

后续还有置信区间的计算过程，仅了解即可…

---

3. 分类的可选技术

3.1 基于规则的分类

分类如果使⽤“if…then…"使⽤下述规则

LHS：规则的前项或前提条件
RHS：规则的结果

例：

规则–>结论

查表得出结论

• 规则的覆盖和准确性

  A:覆盖数字

  D：总共数字

  y：正确的个数

  
  • 覆盖
  
  • 准确性
  

3.1.1 归类如何⼯作

• 基于规则的排序

  • 根据单个规则的质量（覆盖率、准确性、总描述长度…）进行排序择机

• 规则集的特点

  • 互斥（Mutually）
    • -如果规则是相互独立的，分类器就包含相互排斥的规则
    • -每一条记录至多被R中的一条规则覆盖（规则不能被重复使用）
  • 穷举（Exhaustive）
    • 如果分类器考虑到属性值的每一种可能的组合，那么它就有详尽的覆盖范围
    • 每一条记录至少被R中的一条规则覆盖（每个规则都能分到样本）

• 如果规则集不是互斥的，那么一条记录可能被多条规则覆盖，这些规则的预测可能会相互冲突，解决这个问题有如下两种方法
• 有序规则（按照覆盖率、准确率、总描述长度或规则产生的顺序）
• 无序规则（投票规则：多数类或用准确率加权）

如果规则集不是穷举的，必须添加一个默认规则来覆盖那些未被覆盖的记录。默认规则的前件为空，当所有其他规则失效时触发，yd为没有被现存规则覆盖样本的多数类

3.1.2 规则的排序

• 根据规则本身的性能进行排序（例如对于Refund属性：No或者Yes谁在前进行排序）

• 基于类的排序（例如对于结果：No或者Yes谁在前进行排序）

3.1.3 构建分类规则

• 直接生成法
  • 直接从数据中提取规则
  • 比如：RIPPER、CN2、Holle’s 1R
• 间接生成法
  • 基于决策树的分类器
  • 比如：C4.5

3.1.4 规则提取的直接生成法

• 顺序覆盖

  1. 从一个空的规则开始。

  2. 使用Learn-OneRule函数增长一条规则。

  3. 删除规则所涵盖的训练记录。

  4. 重复步骤（2）和（3），直到达到停止标准。

1. Learn-One-Rule函数

是一个分类规则，该规则覆盖训练集中的大量正例。Learn-One-Rule以一种贪心的方式解决搜索中遇到的问题

• 规则增长

  • 两种规则生成策略

    • 一般到特殊
    
    • 特殊到一般
    

• 规则评估

  • FOIL信息增益
  

  P0:R0集合中的正例的数目

  N0:R0集合中的反例的数目

  P1:R1集合中的正例的数目

  N1:R1集合中的反例的数目

2. RIPPER算法

• 对于只有两个类，选择多数类作为正类，少数类一个作为负类，预测少数类的学习规则

• 对于多类问题

  • 首先学习最小的类的规则集，将其余的类作为负类。
  • 重复学习下一个最小的类作为正类

• 生成一个规则

  • 从空规则开始

  • 只要能提高FOIL的信息增益，就增加连接点

  • 当规则开始覆盖负面的例子时停止

  • 修剪规则

  • 修剪的衡量标准：v = (p-n)/(p+n)

    • p:验证集中被规则覆盖的正面例子的数量
    • n:验证集中规则覆盖的负面例子的数量

  • 修剪方法：删除任何使v最大化的最终条件序列

• 构建规则集

  • 使用顺序覆盖算法
    • 找到覆盖当前正例集的最佳规则
    • 消除规则所覆盖的正反两方面的例子
  • 每次向规则集添加规则时，计算新的描述长度
    • 当新的描述长度比最小的描述长度长d比特时，停止添加新的规则
    • 当新的描述长度比目前获得的最小描述长度多出d位时（默认d=64），停止添加新的规则

3.1.5 规则提取的间接法：C4.5（决策树生成）

例如：

• 规则产生

  • 考虑一个替代规则r′：A′ -> y 其中A′是通过删除A中的一个连接点得到的。

  • 将r′的悲观错误率与所有r的悲观错误率进行比较

  • 如果其中一个替代规则的悲观错误率较低，则进行修剪

  • 重复进行，直到我们不能再提高悲观错误率为止

• 规则排序

  • 

例：对比优缺点

	a)The C_4,5 rules algorithm generates classification rules from a global perspective. This is because the rules are derived from decision trees, which are induced with the objective of partitioning the feature space into homogeneous regions, without focusing on any classes. In contract, RIPPER generates rules one-class-at-a-time. Thus, it is more biased towards the classes that are generated first.
	b)The class-ordering scheme used by C_4,5 rules has an easier interpretation than the scheme used by RIPPER. But, RIPPER has the same or higher accuracy, and higher leaning efficiency. 

3.2 最近邻分类器

用最相近的几个事物来预测值

需要三样东西

• 有标签的记录集

• 用于计算记录之间距离的距离指标

• k的值，即要检索的最近的数量

  k=1

  

  k=2

  

对一个未知的记录进行分类。

• 计算与其他训练记录的距离

• 识别k个最近的邻居

• 使用最近邻居的类别标签来确定未知记录的类别标签（例如，通过采取多数投票）。

3.2.1最近邻分类（Nearest Neighbor Classifiers）

• 使用欧氏距离评估相似度（w）

距离越近w越大

• 放缩

可能需要对属性进行缩放，以防止距离测量被某一属性所支配

• 最近邻分类器概述
  • K-NN分类器是消极学习方法，它们没有明确地构建模型
  • 对未知记录进行分类相对昂贵
  • 可以产生任意形状的决策边界
  • 由于决策基于局部信息，因此易于处理变量交互
  • 选择正确的接近度是必要的
  • 多余或多余的属性会产生问题
  • 缺失的属性很难处理

3.3 贝叶斯分类器（求概率X是未知数）重点

3.3.1 贝叶斯定理

3.3.2 贝叶斯定理在分类中的应用

预测一个Y值，使得P(Y| X1, X2,…, X d)的概率最大

例：

估计出条件任意，Evade=Yes/No的概率

理论

1.计算下述概率

2.对于多维（条件不相关）可以进行拆分

例：

解

1. 首先进行公示转化

   

2. 在进行分步求解

   • 
   • 
   • 最后X可以为表中的任何一个属性值，进行查表代入
   

3.3.3 根据数据估计概率

• 对于连续属性：
  • 离散化：可以把每一个连续的属性离散化，然后用相应的离散区间替代连续属性值
  • 概率密度估计
    • 假设属性服从某种概率分布 ，使用数据来估计分布的参数（例如，平均值和标准差）
    • 一旦知道概率分布，就用它来估计条件概率P(Xi |Y)

例如：正态分布（需要提前计算平均值和标准差）

例：

平均数：120

方差：2975

后续例题自行观看

拉普拉斯度量，m度量

• 其他情况

  • 如果一个条件概率是0，整体的表达式也会变成0，需要使用其他估计方法

  c：类的数量

  

例：

问下述条件约束后 该动物是不是哺乳动物

A：4个约束条件

M：是哺乳动物

N：不是哺乳动物

3.3.4 贝叶斯网络（BBN）

定义：用图形表示一组随机变量之间的概率关系

如果将一组随机变量之间的概率关系提供可视化表示，需要：

• 有向无环图

箭头表示条件关系

例如：在Y的条件下X的取值

• 一个概率表

例：

计算右下角的P（）

解：（注意E与D是HD的父亲结点，需要单独计算）

3.4 人工神经网络（ANN）

右边是一个简单的神经网络结构——感知器，ANN用感知器来完成像左边这样简单的输入输出关系。

对于输入和输出，求解出中间的处理过程

单层神经网络（感知器）：

输入结点用来表示输入属性，仅仅把数据传送到链上；输出结点用来提供模型输出，进行计算。也就是一个输入数据，一个输出结果。

在感知器中，每个输入结点都通过一个加权的链连接到输出结点。这个加权的链用来模拟神经元间神经键连接的强度，如右边图上红线边的W1。直观来讲，训练感知器的过程就是在不断调整链的权值，直到感知器能拟合训练数据的输入输出关系。

w：权重（根据具体模型会进行修正）

t：偏执因子（阈值）

sign：自定义函数

例

3.4.1 感知器学习

• w的修正规则

初始化权值(w0, w1, …, wd)

循环

对于每个训练样例(xi, yi)

计算输出f(w, xi)

更新权值W^((k+1) )=W^((k) )+λ[y_i - f(W(k) , x_i )] x_i

直到满足条件

λ：学习率（代表调整值对w的影响）

比如：拉姆达大的时候，差值对w影响较大，相反

例：

局限：由于f(w,x)是输入变量的线性组合，所以决策边界是线性的,如果是非线性可分问题，感知学习算法将会失效

所以需要多层神经网络

3.4.2 Artificial Neural Networks (ANN)

• 人工神经网络结构

神经网络拓扑结构可以从两方面对比：

一种是：

单层网络与多层次的网络

感知器就是一个单层网络结构

多层次网络结构包含隐含层

另一种是：

前馈网络：每一层的结点仅与下一层的结点相连。

递归网络：同一层结点相连或一层的结点连接到前面各层的结点。

• 多层神经网络

隐藏层：输入和输出层之间的中间层。感知器只有输入层和输出层，没有隐含层。这也是单层和多层的区别

更一般的激活函数(sigmoid、linear等)，如右图所示：

线性函数、S型函数、双曲正切函数和符号函数。

但也因为有隐藏神经元，无法直接表示Y与X的关系，所以使用**梯度下降算法（通过求导估计）**估计权（W）值

• 梯度下降法

更新权重公式：

最小化误差的平方和：

激活函数f必须是可微的，对于S型函数来说：

随机梯度下降(立即更新权重)

tips：后续不是重点，了解即可

3.5 支持向量积的分类器

例：

找一个线性超平面(决策边界)来分类数据

下图展示了两个分类结果

B2与B1相比，离数据点较近，比较容易受到噪点影响

所以希望找到一个离两集合最远的分类线

二元分类问题的公式：

两个法向量之间的距离

公式推导：

tips：后续不是重点，了解即可

例：

解：

4.1 Clustering聚类算法

4.1.1 聚类介绍

• 什么是分类：寻找一组对象，使一组中的对象彼此相似

• 什么不是聚类

  • 简单分段
  • 描述查询的结果集
  • 监督分类（带标签的）
  • 关联分析

• 聚类的种类

  • 划分聚类（Partitional Clustering）

  

  • 层次聚类（Hierarchical Clustering）

  

  划分距离的方法：

  • 互斥与非互斥：每个样本属于一个类/每个样本属于多个类
  • 模糊与非模糊聚类：每个物品都有权值，用概率表示，概率高的属于那个类
  • 部分聚类与完全聚类：一部分进行聚类和全部进行聚类

  • 完全分离的聚类

  集群是一组点，集群中的任何点与集群中的每一个点之间的距离都比与集群之外的任何点之间的距离更近(或更相似)

  

  • 基于原型聚类（中心聚类）

  每个点更接近(更相似)中心点

  

  • 基于密度聚类

  将稠密结点进行聚类，之间用稀疏点进行间隔

  

  • 基于目标函数进行聚类

  根据想要的目标函数进行聚类

• 输入的数据对于聚类十分重要

  • 计算相似度的方式，比如：欧氏距离、cos距离
  • 数据的特征可能影响相似度计算
    • 维度
    • 属性类型（连续/离散）
    • 数据分布
  • 噪声与离群点（Noise and Outliers）

4.1.2 聚类算法

K-means

• 是划分聚类算法

  指定K的个数

  每个类需要一个中心（centroid）

  每个结点都要指派个最近的一个类

例：

伪代码（思路）

图示：每一次的迭代过程

每次聚类完后，重新计算中心点

如果每次中心变化不大，可以提前终止迭代

• 复杂度

时间复杂度

• 误差平方和 Sum of Squared Error (SSE)

每个点到中心的距离

mi:中心点

通过增加点的个数可以减小SSE（但是也不能一味增加K）

• 选择初始中心对分类造成的影响

  • 影响分类递归次数
  • 影响聚类结果

  非最优

  初始设置后，3部分互不干涉

  

  较优

  

• 选择中心方法：

  • 如果有两对类，在每个类中设置一对初始中心：

  

  • 多次设置，取SSE最小的结果
  • 使用层次聚类，设置初始中心

• K-means算法的问题

如果密度差距比较大会产生不正确结果

非球形

可能会产生空类

解决方案：

• 选择对上证指数贡献最大的点

• 从集群中选择一个SSE最高的点

• 如果有几个空集群，上面的操作可以重复几次

• 优化方法：二分类

K-means的变体，可以产生分区或分层聚类

例：

伪代码

图示:

DB-scan

可设置半径（epsilon）：1.00

与最小临近结点数量（minPoint）：5

• 是基于密度的算法

定义：在一个特定半径内的点个数

• 核心点：在特定半径内，且周围的点的个数大于minPoint
• 边界点：在核心结点的邻域内，不是核心点，但是周围的点的个数小于minPoint
• 噪声点：非边界点

Hierarchical Clustering（层次聚类算法，重点）

• 分类

  • 凝聚的（Agglomerative）

  从单个点开始，每次将相似的点化为一个簇

  • 分裂的（Divisive）

  从包含所有结点的簇开始，将簇从原来的簇划分出来，直到一个簇包含（1个点/k个簇为止）

使用层次聚类算法：距离矩阵/相似性矩阵

tips：距离表示与相似性表示数值上相反

• 两种表示方式

• 优势
  • 不需要提前指定k（中心点个数）值
  • 可以通过切割得到想要的分类方法

例：

伪代码（思路）

在第五步更新（相似性/邻近度）矩阵会涉及到

结点和簇之间的相似度计算，簇与簇之间的相似度计算

簇与簇之间：

• MIN or single link

使用两个最相似的结点进行度量，作为两个簇的相似度

• MAX or Complete link

使用两个最不相似的结点进行度量，作为两个簇的相似度

• Group Average

使用所有点之间的距离求平均，作为两个簇的相似度

例（仔细思考）：

先给出距离矩阵

使用MIN方法：每次找到最相似的点，合并(MIN方法的取巧做法)

发现（3,6）距离最短，合并后按照该方法进行迭代…

使用MAX方法：两个簇每次找到最不相似的点距离作为簇距离，找最相似的合并

使用Group Average方法：使用所有点之间的距离求平均，作为两个簇的相似度，找到最相似的合并

（每次都需要重新平均值计算距离）

（该例题需要仔细思考！）

tips：一定会考

练习题：

解：

第二问复杂，考试不考

4.2 Association Analysis关联分析（重点）

给定一组数据，根据数据预测数据之间的规则

例：购买牛奶与面包 也会买 鸡蛋和蛋糕

数据集可以写成以下两种方式：

最后总结规律可得

4.2.1 专业术语

• Itemset（项集）

有几个不同的物品就是几项集

3项集

• Support count (支持度技术）

判断一个项集出现的频繁程度

写为：1.表中下述三个出现了2次

• Association Rule（关联规则）

  X推出Y的规则

  例如从牛奶和尿布推出啤酒

  
  • 规则总数（R）

  项集为d个，规则总数为：

  

  • 有两个指标：

    • Support (s)支持度：相当于每个规则出现的频率
    
    • **Confidence ©**置信度
    

    使用这两个标准可以规定大于一个阈值才能被称为：强关联规则，可以避免偶然事件

  例:

  继续看上述表1

  

下图列出了所有项集的出现可能

每一个项集都被称为：候选项（M）

但由于**规则数（R）与候选项（M）**过多，下面要进行优化

---

4.2.2 关联分析的规则

• 两个步骤

  1. 找出频繁项集

  **支持度（S）**要大于最小阈值

  2. 规则的产生

  **置信度（C）**要大于最小阈值

所以，关键是：降低找出频繁项集的计算复杂度

• 减少候选项（M）：重点

• 减少事务集

• 减少比较次数

先验原理（Apriori Algorithm）：减少候选项，找出频繁项集（步骤一）

• 定义

1. 如果一个项集是频繁的，那么所有子集也是频繁的

假如：cde是频繁的，可以判断出：

2. 如果一个项集是非频繁的，那么所有超集也是非频繁的

假如：AB是非频繁的，可以判断出：

例：

还是上面图1，并且给出最小支持度要大于0.6

统计出蛋糕和鸡蛋不符合要求

将不符合条件的去除，保留剩下的组成二项集

列出二项集的置信度

(在删除合并三项集时注意是否有上述表格中的内容)

重复上述步骤…

使用先验原理可以通过减少候选项的个数，加快算法速度

• 运算时候选项优化

  1. 候选项生成

  如果一个二项集和一个一项集进行合并，会产生冗余

  

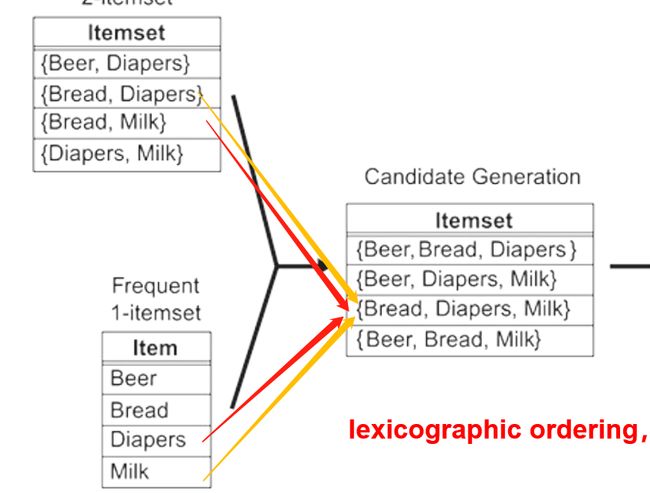
  如果K大于等于3，K-2项集是相同的，K-1进行合并：

  

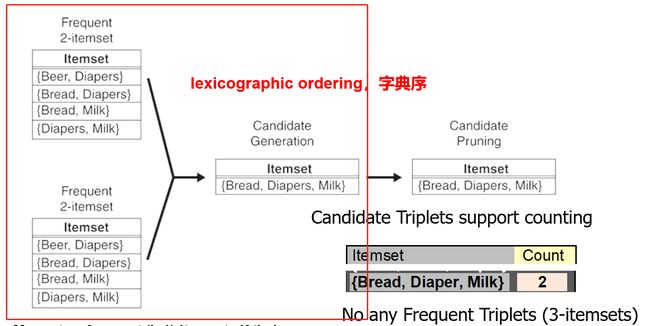
  例：

  求下述频繁3项集合并后的频繁4项集

  如果K>3&前两项集相同，合并：

  

  2. 候选项剪枝

  得到候选4项集，判断子集中是否有非频繁的

  

  最终筛选发现：ABCD符合

  

  3. 支持度记数

  从数据库中获取每一个剩下的候选项的支持度（S）

  4. 检查候选项

  减去不符合要求的支持度的候选项

：规则的生成（步骤二）

一个频繁项集L可以生成许多规则，给出了一个频繁项集L，规则可以写成：

f：L中的一个子集

$$f\to L-f$$

例：

频繁项集为ABCD，生成的规则有：

如果频繁项集L=n个，就有：
$$rules=2^n-2$$
所以数量太多，需要剪枝去筛选

• 定义

如果X的生成规则是不满足置信度（c）的，则其子集也不满足置信度：
$$X\to Y-X\text{\hspace{1em}(不满足置信度)}$$

X`:X的子集

$$X^{‘}\to Y-X^{‘}\text{\hspace{1em}(也不满足置信度)}$$

原理：

如果ABC->D的置信度不满足，后续都不满足

下面列出了所有规则出现的可能：

按照后键进行分层

合并时看后腱

例：

如果BCD->A不满足置信度：

含有BCD子集都会被减去

练习题：

解：

（a）事务表中一共有6个项，因此能够提取的关联规则最大是：R=3^6-2^7+1=602
（b）因为最长的事务包含4个项目，所以频繁项集的最大大小为4。
（c）因为一共有6个项，从该数据集提取3-项集，也就是从6个项中选3个项自由组合，即c_6^3=20