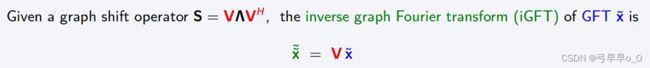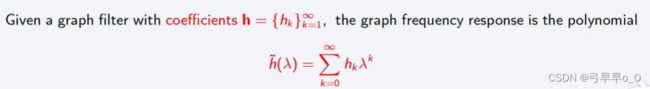GNN笔记系列 3
GNN笔记系列 2
- 1.Graph
-
- 1.1Directed Graphs
- 1.2Symmetric Graphs
- 1.3Unweighted Graphs
- 2.Graph Shift Operators(GSO)
-
- 2.1Degree Matrix
- 2.2Laplacian Matrix
- 2.3Graph Shift Operator S S S
- 3.Graph Signals
- 4.Graph Convolutional Filters
- 5.Time convolutions and graph convolutions
- 6.Graph Fourier Transform
-
- 6.1Graph Fourier Transform
- 6.2Graph Frequency Response
-
- Definition(Frequency Response of a Graph Filter)
1.Graph
图的相关定义可以在这篇文章中看到：
图的介绍及Python实现
1.1Directed Graphs
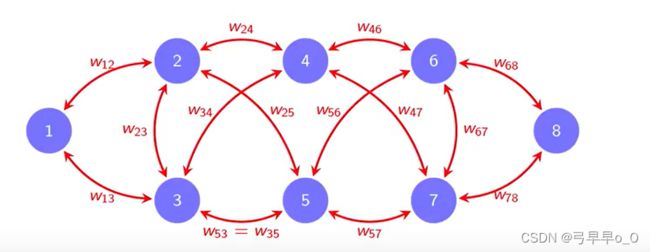
在有向图中，边 ( i , j ) (i,j) (i,j)与 ( j , i ) (j,i) (j,i)是不相同的。
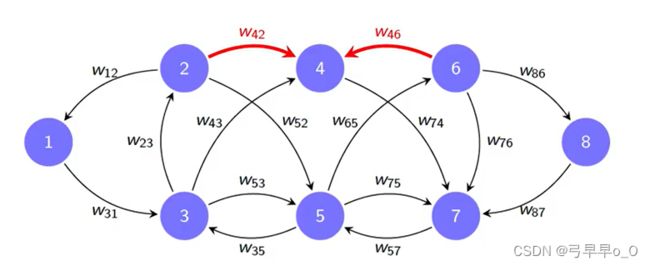
在上图中，可以看到， w i j w_{ij} wij指的是从顶点 j j j到顶点 i i i的权值。这里要注意： w i j w_{ij} wij不一定与 w j i w_{ji} wji相等。
1.2Symmetric Graphs
对称图：权值对称，边也是对称的。
如果边 ( i , j ) (i,j) (i,j)属于边集，那么边 ( j , i ) (j,i) (j,i)也要属于边集。
对于所有的边 ( i , j ) (i,j) (i,j)，都必须有 w i j = w j i w_{ij} = w_{ji} wij=wji.
1.3Unweighted Graphs
无权图：没有权重或者说权重为1。
无权图也可以是有向图或对称图。
2.Graph Shift Operators(GSO)
在信号处理中，图的矩阵表示称为图移位算子。
对于所有的边 ( i , j ) (i,j) (i,j)，有 A i j = w i j A_{ij} = w_{ij} Aij=wij，同时 A i i = w 0 A_{ii} = w_{0} Aii=w0.如果图是对称图，邻接矩阵就是对称阵，那么此时有 A = A T A = A^T A=AT。
下面举一个邻接矩阵的例子：
对于无权图，邻接矩阵有如下性质：
A i i = w 0 A_{ii} = w_{0} Aii=w0，同时对于所有的边 ( i , j ) (i,j) (i,j),有 A i j = 1 A_{ij} = 1 Aij=1。
2.1Degree Matrix
节点的度数等于该节点的邻接权值之和。
2.2Laplacian Matrix
邻接矩阵和拉普拉斯矩阵的规范化形式也被用作图的矩阵表示。
标准化邻接矩阵： A ‾ : = D − 1 / 2 A D − 1 / 2 \overline A:=D^{-1/2}AD^{-1/2} A:=D−1/2AD−1/2
( A ‾ ) i j = w i j d i d j (\overline A)_{ij}=\frac{w_{ij}}{\sqrt {d_id_j}} (A)ij=didjwij标准化拉普拉斯矩阵： L ‾ : = D − 1 / 2 L D − 1 / 2 \overline L:=D^{-1/2}LD^{-1/2} L:=D−1/2LD−1/2
L ‾ : = D − 1 / 2 ( D − A ) D − 1 / 2 = I − A ‾ \overline L:=D^{-1/2}(D-A)D^{-1/2}=I-\overline A L:=D−1/2(D−A)D−1/2=I−A
2.3Graph Shift Operator S S S
邻接矩阵： S = A S=A S=A
拉普拉斯矩阵： S = L S=L S=L
标准化邻接矩阵： S = A ‾ S=\overline A S=A
标准化拉普拉斯矩阵： S = L ‾ S=\overline L S=L
3.Graph Signals
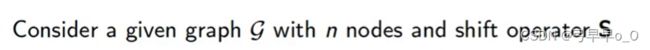
一个图信号就是一个向量 x ∈ R n x\in R^n x∈Rn,分量 x i x_i xi和节点 i i i相关联。
将图定义为一个序对 ( S , x ) (S,x) (S,x).图信号与移位运算符的相乘实现了信号在图上的传播。将传播信号定义为 y = S x y=Sx y=Sx
y i = ∑ j ∈ n ( i ) w i j x j = ∑ j w i j x j y_i=\sum_{j \in n(i)} w_{ij}x_{j} = \sum_jw_{ij}x_{j} yi=j∈n(i)∑wijxj=j∑wijxj x j x_{j} xj是属于节点 i i i的相邻节点 j j j上支持的输入信号 x x x.
注意：
1.大的权值会更容易影响传播信号的值。
2.传播信号是一个局部操作，当前节点与邻近节点的信号混合。
通过移位算子 S S S的递归乘法来定义传播序列：
x ( k + 1 ) = S x ( k ) , x ( 0 ) = x x^{(k+1)}=Sx^{(k)},x^{(0)} = x x(k+1)=Sx(k),x(0)=x传播序列的第0个分量就是图本身。
也可以通过移位运算符的幂乘法来定义该序列：
x ( k ) = S k x x^{(k)}=S^{k}x x(k)=Skx
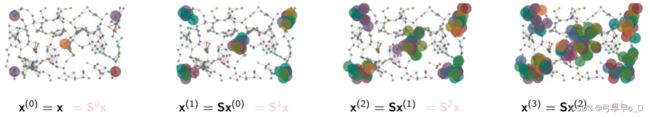
k在小的时候， x ( k ) x^{(k)} x(k)表示局部信息，k在大的时候， x ( k ) x^{(k)} x(k)就表示全局信息了。
对传播序列的两种定义（1是移位运算符的递归定义，2是移位运算符的幂乘定义），在实现时使用递归版本，当考虑分布式系统时，只能选择递归版本。幂乘版本在分析时比较好用。
4.Graph Convolutional Filters
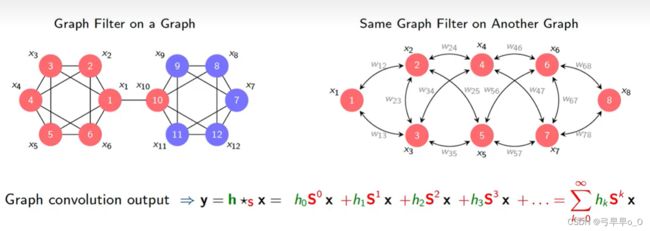
图卷积滤波器是图信号线性处理的首选工具。给定一个图移位算子 S S S和系数 h k h_k hk，图卷积滤波器是一个关于 S S S的多项式序列:
H ( S ) = ∑ k = 0 ∞ h k S k H(S)=\sum_{k=0}^ \infty h_kS^k H(S)=k=0∑∞hkSk.将滤波器 H ( S ) H(S) H(S)应用到信号 x x x上的结果维输出信号 y y y： y = H ( S ) x = ∑ k = 0 ∞ h k S k x y=H(S)x=\sum_{k=0}^ \infty h_kS^kx y=H(S)x=k=0∑∞hkSkx.将 y = h ∗ S x y=h_{*_{S}}x y=h∗Sx为滤波器 h = h k ∣ k = 0 ∞ h={h_k}|_{k=0}^{\infty} h=hk∣k=0∞和图信号 x x x的图卷积。
图卷积将信息从局部邻域聚合为全局邻域。
同一个滤波器可以在多个不同的图中执行。
在右边的另一幅图中，虽然图卷积的公式看起来没有什么不同，但是其实结果是有差别的。原因就在于每一个节点的相邻节点都不同。
图卷积其实就是传播序列的元素的加权线性组合。
Shift：就是用移位算子S对输入信号x作幂乘。
Scale：就是用缩放系数h对S作乘法。
Sum：就是求和。
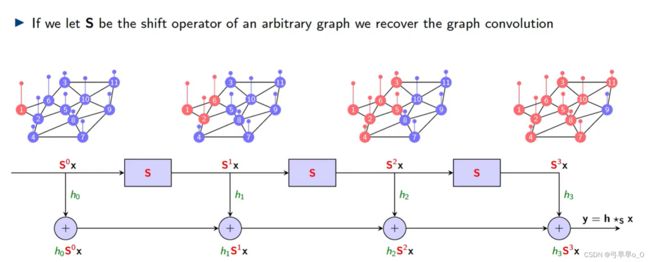
下图展示了图卷积的过程：
5.Time convolutions and graph convolutions
时间卷积是图卷积的特例。
在以上寄存器中，出现的所有时间
时间信号可以表示为线图上支持的图信号时间移位可以表示为该图邻接矩阵的乘法。
时间移位可以等价表述线图上邻接矩阵的乘积。
因此，可以将时间卷积滤波器重写为线图邻接矩阵多项式的乘法。
另外一个图的卷积运算：
6.Graph Fourier Transform
这里研究对称图，它具有 S = S H S=S^H S=SH的对称移位运算符。
6.1Graph Fourier Transform
傅里叶变换：
对以上定义的解释是：信号x的傅里叶变换是它在移位算子的本征向量基上的投影。
graph frequency representation : 图频表示。
逆傅里叶变换：
6.2Graph Frequency Response
在图频域中投影时，图滤波器允许逐点表示。
图滤波器的图频表示定理：
定义图滤波器的变量是 S S S，定义频率的变量是大 λ \lambda λ矩阵。但它们的系数是一样的。
Definition(Frequency Response of a Graph Filter)
