【RL】策略梯度(VPG)与Actor-critic的思想与推导
获取更多内容,请访问博主的个人博客 爱吃猫的小鱼干的Blog
一 RL学习什么
-
动作值函数(Q函数)。
以Q-Learning、DQN为代表,这个系列的算法学习最优动作值函数 Q ∗ ( s , a ) Q^*(s,a) Q∗(s,a) 的近似函数 Q θ ( s , a ) Q_\theta(s,a) Qθ(s,a) 。
Q-learning 智能体的动作由下面的式子给出:
a ( s ) = arg max a Q θ ( s , a ) a(s)=\arg\,\max_a\, Q_\theta(s,a) a(s)=argamaxQθ(s,a)
-
策略(随机或确定的)。
这个系列的方法将策略显示表示为 π w ( a ∣ s ) \pi_{w}(a \mid s) πw(a∣s) ,它们直接对性能目标 J ( π w ) J(\pi_{w}) J(πw) 进行梯度下降来优化参数 w w w ,使得我们输入当前的 s s s 就能输出应该执行的最佳动作 a a a 。
-
值函数。
-
以及/或者环境模型。
二 Vanilla Policy Gradient(VPG)
以下考虑的情况是状态 s s s 为连续高维变量、动作 a a a 为分类变量(有限个)的MDP。并且,设环境 P s , s ′ a P_{s, s^{\prime}}^{a} Ps,s′a 与 r 5 a r_{5}^{a} r5a 为时齐的,不随时间的变化而变化。(状态与动作都是连续变量的MDP有更高效的DDPG等方法解决,不在VPG里讨论)
2.1 策略网络的构造
在随机且时齐的MDP中,策略是状态到动作的映射。由于 a a a 是分类变量,所以没有办法直接输出 a a a ,只能输出一个条件分布 π ( a ∣ s ) \pi(a \mid s) π(a∣s) 。为了拟合这个策略,我们定义一个神经网络policy net。网络的输入是 s s s ,输出是一个 n n n 维向量,对它进行softmax之后,得到 n n n 个不同的概率(其和为1),分别对应于最佳动作是各个 a a a 的概率。设网络的参数为 w w w ,则可以将网络输出简记为 π w ( a ∣ s ) \pi_{w}(a \mid s) πw(a∣s) ,它表示在 s s s 状态下最佳动作是 a a a 的条件概率。
与我们熟悉的分类网络做比较:
我们可以认为分类网络是在用“权重相同的训练集”去训练,而策略网络则是在用“带有不同权重的训练集”去训练。只要我们能够找出衡量 ( s , a ) (s,a) (s,a) 好坏的标准. v v v ,得到形式 ( s , a , v ) (s,a,v) (s,a,v) 的数据,就可以把训练策略网络的过程看成“带权重的监督学习”。但是,我们如何找出这个 v v v 呢?找出之后具体 v v v 应该按照什么公式训练呢?下面,要详细地根据定义推导出policy gradient的表达式。
2.2 推导最基本的策略梯度
接下来推导策略梯度的公式及其计算方法。
假设策略网络的参数为 w w w ,则可以将策略记为 π w \pi_w πw 。
- 轨迹的概率。在不同网络参数 w w w 下,策略 π w \pi_w πw 给出的轨迹 τ = ( s 0 , a 0 , r 0 , s 1 , a 1 , r 1 , s 2 , a 2 , r 2 , … , s t , a t , r t ) \tau = \left(s_{0}, a_{0}, r_{0}, s_{1}, a_{1}, r_{1}, s_{2}, a_{2}, r_{2}, \ldots, s_{t}, a_{t}, r_{t}\right) τ=(s0,a0,r0,s1,a1,r1,s2,a2,r2,…,st,at,rt) 有不同的分布 P π w ( τ ) P_{\pi_{w}}(\tau) Pπw(τ) ,简记为 P w ( τ ) P_{w}(\tau) Pw(τ) 。
P w ( τ ) = Π t = 0 n π w ( a t ∣ s t ) Π t = 0 T − 1 P s t , s t + 1 a t Π t = 0 T P ( r t ∣ s t , a t ) P_{w}(\tau)=\Pi_{t=0}^{n} \pi_{w}\left(a_{t} \mid s_{t}\right) \Pi_{t=0}^{T-1} P_{s_{t}, s_{t+1}}^{a_{t}} \Pi_{t=0}^{T} P\left(r_{t} \mid s_{t}, a_{t}\right) Pw(τ)=Πt=0nπw(at∣st)Πt=0T−1Pst,st+1atΠt=0TP(rt∣st,at)
- 目标函数。我们的目标是最大化期望回报 J ( w ) = E w ( r ( τ ) ) J(w)=E_{w}(r(\tau)) J(w)=Ew(r(τ)) ,这里假设回报无衰减( γ = 1 \gamma=1 γ=1 ,对于 γ < 1 \gamma<1 γ<1 的情况推导过程类似)。
J ( w ) = E w ( r ( τ ) ) = ∫ τ P w ( τ ) r ( τ ) d τ J(w) = E_{w}(r(\tau)) = \int_{\tau} P_{w}(\tau) r(\tau) d \tau J(w)=Ew(r(τ))=∫τPw(τ)r(τ)dτ
- 策略梯度。我们想求的“策略梯度”就是 ∇ w J ( w ) \nabla_{w} J(w) ∇wJ(w) 。得到策略梯度就可以通过梯度下降来优化策略 w k + 1 = w k + α ∇ w J ( w ) w_{k+1} = w_{k} + \alpha\,\nabla_{w} J(w) wk+1=wk+α∇wJ(w) 。
∇ w J ( w ) = ∫ τ ( ∇ w P w ( τ ) ) r ( τ ) d τ \nabla_{w} J(w)=\int_{\tau}\left(\nabla_{w} P_{w}(\tau)\right) r(\tau) d \tau ∇wJ(w)=∫τ(∇wPw(τ))r(τ)dτ
上面的 ∇ w J ( w ) \nabla_{w} J(w) ∇wJ(w)仍然是一个积分式,我们很自然地希望将其表示为 ∫ τ P w ( τ ) ∇ w f ( τ ) d τ \int_{\tau} P_{w}(\tau) \nabla_{w} f(\tau) d \tau ∫τPw(τ)∇wf(τ)dτ的形式,其中的 f f f是某 个函数。根据期望的定义,这个积分的结果就是 E w [ ∇ w f ( τ ) ] E_{w}\left[\nabla_{w} f(\tau)\right] Ew[∇wf(τ)]。这样的形式更加简便,并且也更容易计算—— 只要我们用当前的策略与环境交互采样很多 τ \tau τ,并计算出梯度 ∇ w f ( τ ) \nabla_{w} f(\tau) ∇wf(τ)的均值,就能将其作为 ∇ w J ( w ) \nabla_{w} J(w) ∇wJ(w)的一个 估计。
- 对数导数技巧。
P w ( τ ) ∇ w log P w ( τ ) = P w ( τ ) ∇ w P w ( τ ) P w ( τ ) = ∇ w P w ( τ ) P_{w}(\tau) \nabla_{w} \log P_{w}(\tau)=P_{w}(\tau) \frac{\nabla_{w} P_{w}(\tau)}{P_{w}(\tau)}=\nabla_{w} P_{w}(\tau) Pw(τ)∇wlogPw(τ)=Pw(τ)Pw(τ)∇wPw(τ)=∇wPw(τ)
将 (5) 带入 (4) 得:
∇ w J ( w ) = ∫ γ ( ∇ w P w ( τ ) ) r ( τ ) d τ = ∫ γ P w ( τ ) ∇ w log ( P w ( τ ) ) r ( τ ) d τ = E w [ ∇ w log ( P w ( τ ) ) r ( τ ) ] \nabla_{w} J(w) = \int_{\gamma}\left(\nabla_{w} P_{w}(\tau)\right) r(\tau) d \tau \\= \int_{\gamma} P_{w}(\tau) \nabla_{w} \log \left(P_{w}(\tau)\right) r(\tau) d \tau \\= E_{w}\left[\nabla_{w} \log \left(P_{w}(\tau)\right) r(\tau)\right] ∇wJ(w)=∫γ(∇wPw(τ))r(τ)dτ=∫γPw(τ)∇wlog(Pw(τ))r(τ)dτ=Ew[∇wlog(Pw(τ))r(τ)]
- 环境函数的梯度。环境不依赖于参数 w w w ,所以式 (2) 中 P s i , s i + 1 a i P_{s_{i}, s_{i+1}}^{a_{i}} Psi,si+1ai , P ( r i ∣ s i , a i ) P\left(r_{i} \mid s_{i}, a_{i}\right) P(ri∣si,ai) 的梯度为零。
- 轨迹对数概率的梯度。所以轨迹对数概率的梯度为:
∇ w log ( P w ( τ ) ) = ∑ t = 0 T ∇ w log π w ( a t ∣ s t ) \nabla_{w} \log \left(P_{w}(\tau)\right)=\sum_{t=0}^{T} \nabla_{w} \log \pi_{w}(a_{t} \mid s_{t}) ∇wlog(Pw(τ))=t=0∑T∇wlogπw(at∣st)
- 简化后的基本策略梯度。
∇ w J ( w ) = E w [ ∑ t = 0 T ∇ w log π w ( a t ∣ s t ) r ( τ ) ] \nabla_{w} J(w)=E_{w} \left[\sum_{t=0}^{T} \nabla_{w} \log \pi_{w}\left(a_{t} \mid s_{t}\right)r(\tau) \right] ∇wJ(w)=Ew[t=0∑T∇wlogπw(at∣st)r(τ)]
这是一个期望,这意味着我们可以使用样本均值对其进行估计。 如果我们收集一组轨迹 D = { τ i } i = 1 , ⋯ , N D = {\left\{ \tau_i \right\}}_{i=1,\cdots,N} D={τi}i=1,⋯,N , 其中每一个轨迹通过让智能体在环境中使用策略 π w \pi_w πw 执行操作得到,则策略梯度可以使用以下式子进行估计:
g ^ = 1 N ∑ τ ∈ D ∑ t = 0 T ∇ w log π w ( a t ∣ s t ) r ( τ ) \hat{g} = \frac{1}{N}\sum_{\tau \in D} \sum_{t=0}^{T} \nabla_{w} \log \pi_{w}\left(a_{t} \mid s_{t}\right)r(\tau) g^=N1τ∈D∑t=0∑T∇wlogπw(at∣st)r(τ)
2.3 VPG算法
| Policy gradient |
|---|
| 构建策略网络 π w ( a ∣ s ) \pi_{w}(a \mid s) πw(a∣s) ,并随机初始化参数 |
| 重复下面步骤: |
| 用策略 π w ( a ∣ s ) \pi_{w}(a \mid s) πw(a∣s) 与环境交互,产生大量 τ \tau τ |
| 计算 ∇ w log π w ( a t ∣ s t ) r ( τ ) \nabla_{w} \log \pi_{w}\left(a_{t} \mid s_{t}\right)r(\tau) ∇wlogπw(at∣st)r(τ) 的均值,作为策略梯度 ∇ w J ( w ) \nabla_wJ(w) ∇wJ(w) 的估计 |
| 让 w w w 沿着策略梯度的方向前进: w = w + α ∇ w J ( w ) w = w + \alpha\,\nabla_{w} J(w) w=w+α∇wJ(w) |
| 直到收敛 |

三 Actor-Critic
3.1 AC的出发点
上述策略梯度式 (7) 可以理解为:“用带有权重的训练集去训练策略网络”,对于每一步决策,我们用一个能衡量这步决策好坏的“学习权重” r ( τ ) r(\tau) r(τ) 去”促进“或”抑制“当前轨迹 τ \tau τ 上的所有决策 π w ( a ∣ s ) \pi_{w}(a \mid s) πw(a∣s) 。 r ( τ ) > 0 r(\tau)>0 r(τ)>0 ,则”促进“这个轨迹上的所有策略; r ( τ ) < 0 r(\tau)<0 r(τ)<0 ,则”抑制“这个轨迹上的所有策略。
但是,即使 r ( τ ) > 0 r(\tau)>0 r(τ)>0 ,轨迹 τ \tau τ 上也有可能出现少量差的决策,如果采用上面的方法,会同时”促进“这些差的决策。在采样样本比较有限的情况下,这可能会导致巨大的均方误差。
一个最自然的想法是,我们不应该将一个 τ \tau τ 上所有 ( s , a ) (s, a) (s,a) 编成一个batch,用一个统一的“权重” r ( τ ) r(\tau) r(τ) 来衡量它们的好坏。而应该找出一个“权重”能够单独衡量每一个 ( s , a ) (s, a) (s,a) 的好坏。
3.2 对策略梯度的优化
3.2.1 不要受过去的影响(Don’t Let the Past Distract You)
回顾我们的策略梯度表达式(7) ,他将“轨迹”上每个动作的对数概率都乘了一个“权重” r ( τ ) r(\tau) r(τ) (曾经与将来所有奖励的总和)。
但这没有多大意义。智能体实际上仅应根据其采取动作后的 结果 强化动作。采取动作之前获得的奖励与该动作的效果无关。这种直觉体现在数学上,可以证明策略梯度也可以表示为:
∇ w J ( w ) ≈ E w [ ∑ t = 0 T ∇ w log π w ( a t ∣ s t ) ∑ t ‘ = t T R ( s t ′ , a t ′ , s t ′ + 1 ) ] ≈ E w [ ∑ t = 0 T ∇ w log π w ( a t ∣ s t ) Q ^ ( s t , a t ) ] \nabla_{w} J(w) \approx E_{w} \left[\sum_{t=0}^{T} \nabla_{w} \log \pi_{w}\left(a_{t} \mid s_{t}\right) \sum_{t‘=t}^{T}R(s_{t'},a_{t'},s_{t'+1}) \right] \\\approx E_{w} \left[\sum_{t=0}^{T} \nabla_{w} \log \pi_{w}\left(a_{t} \mid s_{t}\right) \hat{Q}(s_t,a_t) \right] ∇wJ(w)≈Ew[t=0∑T∇wlogπw(at∣st)t‘=t∑TR(st′,at′,st′+1)]≈Ew[t=0∑T∇wlogπw(at∣st)Q^(st,at)]
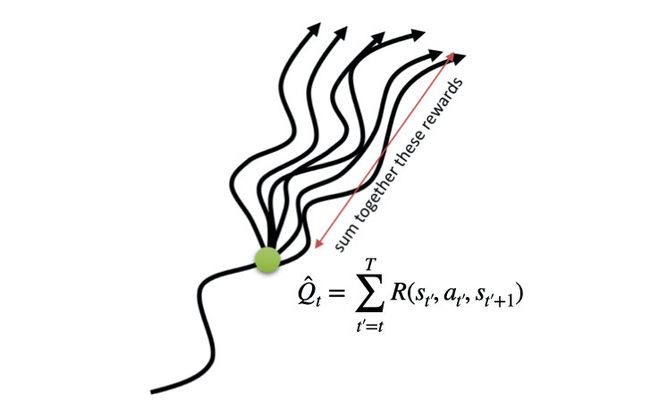
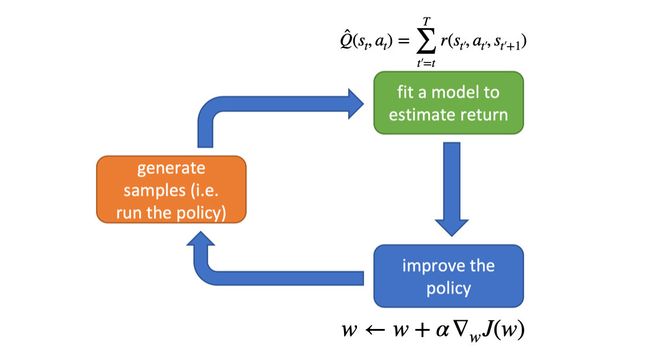
为什么这样做会更好?策略梯度的关键问题是需要多少个样本轨迹才能获得它们的低方差样本估计。 我们从公式开始就包括了与过去的奖励成比例的强化动作的项, 它们均值为零,但方差不为零:导致它们只会给策略梯度的样本估计值增加噪音。 通过删除它们,减少了所需的样本轨迹数量。
3.2.2 Q ^ ( s t , a t ) \hat{Q}(s_t,a_t) Q^(st,at) 的Baseline
式 (9) 用当前动作的”状态-动作“价值函数的估计 Q ^ ( s t , a t ) \hat{Q}(s_t,a_t) Q^(st,at) 作为衡量本次决策的”权重“,看起来是很合适的,但是必须考虑这样一种情形:在回报都是大于零的环境中(例如贪吃蛇游戏,把游戏结束时蛇身的长度作为回报), Q ^ ( s t , a t ) \hat{Q}(s_t,a_t) Q^(st,at) 会是恒正的值,按照上面的思路,即使是一个很差的决策(例如游戏结束时蛇身长为3),策略梯度也会在”权重“ Q ^ ( s t , a t ) \hat{Q}(s_t,a_t) Q^(st,at) 的作用下比较缓慢的”促进“这个决策。
但是,如果我们采样了 N N N 条轨迹,就可以用 Q ^ ( s t , a t ) \hat{Q}(s_t,a_t) Q^(st,at) 减去自己的均值,使得比均值小的 Q ^ ( s t , a t ) \hat{Q}(s_t,a_t) Q^(st,at) 变为负,比均值大的 Q ^ ( s t , a t ) \hat{Q}(s_t,a_t) Q^(st,at) 变为正,”赏罚分明“的进行训练策略。
那么,给式 (9) 策略梯度的 Q ^ ( s t , a t ) + b ( s t ) \hat{Q}(s_t,a_t)+b(s_t) Q^(st,at)+b(st) 后该式还成立吗?可以证明它仍然是成立的。
由ELPG引理可得:
E w [ ∇ w log ( P w ( x ) ) b ] = ∫ x ∇ w P w ( x ) b d x = b ∇ w ∫ x P w ( x ) d x = 0 E_{w}\left[\nabla_{w} \log \left(P_{w}(x)\right) b\right]=\int_{x} \nabla_{w} P_{w}(x)b\ dx = b \nabla_{w} \int_{x} P_{w}(x)\ dx=0 Ew[∇wlog(Pw(x))b]=∫x∇wPw(x)b dx=b∇w∫xPw(x) dx=0
所以:
∇ w J ( w ) ≈ E w [ ∑ t = 0 T ∇ w log π w ( a t ∣ s t ) ( Q ^ ( s t , a t ) − b ( s t ) ) ] \nabla_{w} J(w) \approx E_{w} \left[\sum_{t=0}^{T} \nabla_{w} \log \pi_{w}\left(a_{t} \mid s_{t}\right) \left(\hat{Q}(s_t,a_t)-b(s_t)\right) \right] ∇wJ(w)≈Ew[t=0∑T∇wlogπw(at∣st)(Q^(st,at)−b(st))]
其中 b ( s t ) = 1 N ∑ i N Q i , t b(s_t)=\frac{1}{N} \sum_i^N Q_{i,t} b(st)=N1∑iNQi,t ,它可以看作是对状态值函数 V ( s t ) = E w ( Q ( s t , a t ) ) V(s_t)=E_w(Q(s_t,a_t)) V(st)=Ew(Q(st,at)) 的估计,因此策略梯度可以表示为:
∇ w J ( w ) ≈ E w [ ∑ t = 0 T ∇ w log π w ( a t ∣ s t ) ( Q ^ ( s t , a t ) − V ( s t ) ) ] \nabla_{w} J(w) \approx E_{w} \left[\sum_{t=0}^{T} \nabla_{w} \log \pi_{w}\left(a_{t} \mid s_{t}\right) \left(\hat{Q}(s_t,a_t)-V(s_t)\right) \right] ∇wJ(w)≈Ew[t=0∑T∇wlogπw(at∣st)(Q^(st,at)−V(st))]
而由Bellman Equation知道: A ( s t , a t ) = Q ( s t , a t ) − V ( s t ) A(s_t,a_t)=Q(s_t,a_t)-V(s_t) A(st,at)=Q(st,at)−V(st) ,因此策略梯度又可以表示为:
∇ w J ( w ) ≈ E w [ ∑ t = 0 T ∇ w log π w ( a t ∣ s t ) A ( s t , a t ) ] \nabla_{w} J(w) \approx E_{w} \left[\sum_{t=0}^{T} \nabla_{w} \log \pi_{w}\left(a_{t} \mid s_{t}\right) A(s_t,a_t) \right] ∇wJ(w)≈Ew[t=0∑T∇wlogπw(at∣st)A(st,at)]
由于:
Q ( s t , a t ) = r ( s t , a t ) + V ( s t + 1 ) A ( s t , a t ) ≈ r ( s t , a t ) + V ( s t + 1 ) − V ( s t ) Q(s_t,a_t) = r(s_t,a_t)+V(s_{t+1}) \\ A(s_t,a_t) \approx r(s_t,a_t)+V(s_{t+1})-V(s_{t}) Q(st,at)=r(st,at)+V(st+1)A(st,at)≈r(st,at)+V(st+1)−V(st)
所以,计算策略梯度式(12) 的关键是计算 V ( s t ) V(s_t) V(st) 。实际上,无法精确计算 V ( s t ) V(s_t) V(st) ,通常这是通过神经网络 V ϕ ( s t ) V_{\phi}(s_t) Vϕ(st) 来近似的(Value net)。该神经网络会与策略同时进行更新(以便价值网络始终近似于最新策略的值函数)。
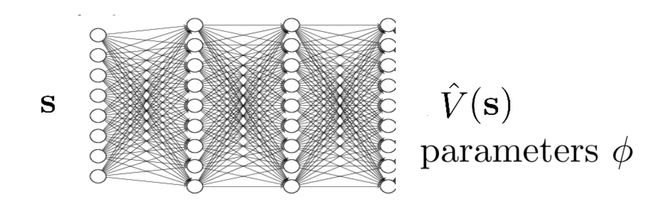
3.3.3 Value net怎么更新
Value net的目的是估计 V ( s t ) V(s_t) V(st) ,那么最小化它们之间的均方误差就可以作为一个监督信号,用来在神经网络中反向传播学习 V ϕ V_{\phi} Vϕ 。
L ( ϕ ) = 1 N ∑ i N ∥ V ϕ ( s i , t ) − V ( s i , t ) ∥ 2 = 1 N ∑ i N ∥ V ϕ ( s i , t ) − ( r ( s i , t , a i , t ) + V ϕ ( s i , t + 1 ) ) ∥ 2 L(\phi) = \frac{1}{N}\sum_{i}^{N} {\left\| V_{\phi}(s_{i,t})-V(s_{i,t}) \right\|}^2 \\= \frac{1}{N}\sum_{i}^{N} {\left\| V_{\phi}(s_{i,t})-\left(r(s_{i,t},a_{i,t})+V_{\phi}(s_{i,t+1})\right) \right\|}^2 L(ϕ)=N1i∑N∥Vϕ(si,t)−V(si,t)∥2=N1i∑N∥Vϕ(si,t)−(r(si,t,ai,t)+Vϕ(si,t+1))∥2
至此,Value net可以通过训练,很好的估计 V ( s t ) V(s_t) V(st) 。将它替代VPG中的 r ( τ ) r(\tau) r(τ) 作为”权重“,指引策略网络学习最优策略。同时也达到了本节开始提出的目的——找出一个能够单独衡量每一个 ( s , a ) (s, a) (s,a) 好坏的“权重”。

3.3 Actor-Critic算法
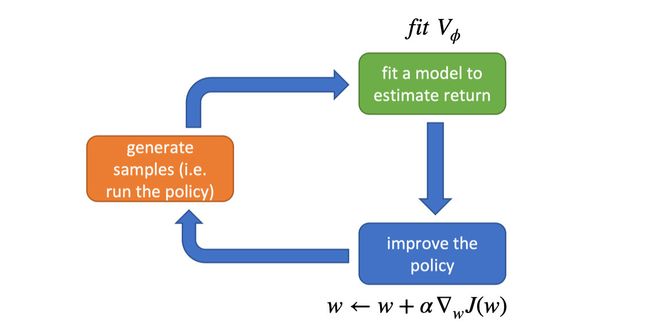
AC算法的大体框架是这样的:我们定义两个神经网络:一个是用来计算 V ϕ ( s t ) V_{\phi}(s_t) Vϕ(st) 价值网络,另一个则是策略网络。我们用策略网络与环境交互产生许多数据集,并用这些数据集同时训练两个网络,提升网络的性能。
| Actor-Critic |
|---|
| 构造并初始化Value net的参数 w w w 和Policy net的参数 ϕ \phi ϕ |
| 重复以下步骤: |
| 通过Policy net与环境交互产生数据集 ( s , a , r , s ′ ) (s,a,r,s') (s,a,r,s′) |
| 训练Value net:让 ϕ \phi ϕ 沿着使损失 L ( ϕ ) = ∥ V ϕ ( s ) − ( r + V ϕ ( s ′ ) ) ∥ 2 L(\phi)=\left\| V_{\phi}(s)-(r+V_{\phi}(s')) \right\|^2 L(ϕ)=∥Vϕ(s)−(r+Vϕ(s′))∥2 下降的方向前进 |
| 训练Pollicy net:让 w w w 沿着梯度 ∇ w J ( w ) \nabla_wJ(w) ∇wJ(w) 的方向前进 |
| 直到收敛 |
获取更多内容,请访问博主的个人博客 爱吃猫的小鱼干的Blog

