2018年苏州大学872真题整理

一. 数据结构部分

1、（15 分）判断题，判断下列说法是否正确，如错误，指出错误之处。
（1）对于哈希（散列）查找，若采用线性探测法解决冲突，则装填因子 α 可以大于 1。
错误；线性探测时，散列表中的元素个数不可能超过表长度；拉链法α可以大于1
（2）在 AVL 树上进行查找，平均查找长度为$O(lo{g}_{2}n)$ 。
正确
（3）一棵完全二叉树的高度为 h，则该树至少有$2^{h-1}$个结点。
正确；$h-1$层的满二叉树 + 1个节点 = $2^{h-1}$
（4）一个线性表，如果在对其进行操作的过程中表的长度经常发生变化，则采用顺序存储结构较合适。
错误；顺序结构发生删除增加操作时效率不如链表结构
（5）在使用后缀表达式计算表达式值时，应用队列存放操作数和操作符。
错误；后缀表达式规则：从左到右遍历表达式的每个数字和符号，遇到是数字就进栈，遇到是符号，就将处于栈顶两个数字出栈，进行运算，运算结果进栈，一直到最终获得结果。所以应当使用栈，而不是队列。

2、（15 分）若要对一个序列进行排序，且需要对其进行$O(1)$次插入操作，以及$O(n)$次查找最大值的操作。现有堆和二叉排序树两种数据结构，分别从平均情况和最坏情况下分析各数据结构的时间复杂度。

（1）若考虑平均情况，则应采用哪种数据结构，时间复杂度分别为多少，并进行分析。
采用二叉排序树；查找最大值则需访问最右的子树，时间复杂度为$O(lo{g}_{2}n)$；就插入时维护表的有序性而言，只需修改指针即可完成插入操作，平均的执行时间为$O(lo{g}_{2}n)$；而堆的查找时间复杂度为$O(nlo{g}_{2}n)$，插入时间复杂度为$O(h)$

（2）若考虑最坏情况，则应采用哪种数据结构，时间复杂度分别为多少，并进行分析。
采用堆；因为若待排序的序列已经有序，则二叉排序树会退化为一个链表，查询的效率非常低下，查找最大值（逐一搜索到最右的子树）的时间复杂度为$O(n)$；而堆排序（假设为大根堆）在查找最大值时，只需弹出堆顶的元素即为最大值，则查找的效率为$O(1)$，弹出后的维护时间开销为$O(h)$，则总的时间复杂度为$O(1+h)$；对于插入操作，二叉排序树时间复杂度为$O(n)$，堆的时间复杂度为$O(h)$

3、（15 分）一个线性表的元素均为正整数，使用带头指针的单链表实现。编写算法：判断该线性表是否符合：所有奇数在前面，偶数在后面。

"""
链表的遍历
"""
class Node:
	def __init__(self, data):
		self.data = data
		self.next = None

def isValidate(head: Node): -> bool
	even = False
	while head != None:
		head = head.next
		if head.data % 2 == 0 and not even:
			# 遇到第一个偶数
			even = True
		if head.data % 2 == 1 and even:
			return False

	return True

4、（15 分）一棵用二叉链表实现的二叉树，其每个结点包括以下部分内容：结点值 data，左孩子lchild 和右孩子 rchild，还有一个 size 存储该结点子树上的结点总数，现 size 还未赋值。编写算法：为 size 赋值。

"""
	递归题
"""
class TNode:
	def __init__(self, data):
		self.data = data
		self.lchild = None
		self.rchild = None
		self.size = None

def setSizeInTree(root: TNode)
	if root is None:
		return -1
	root.size = setSizeInTree(root.lchild) + setSizeInTree(root.rchild) + 2
	return root.size

5、（15 分）一棵采用孩子-兄弟表示法的树，编写算法：统计树中度为 k 的结点的个数。

孩子-兄弟表示法的树的定义为：树/森林的节点只保留其左子树，并连接其所有的右兄弟。

"""
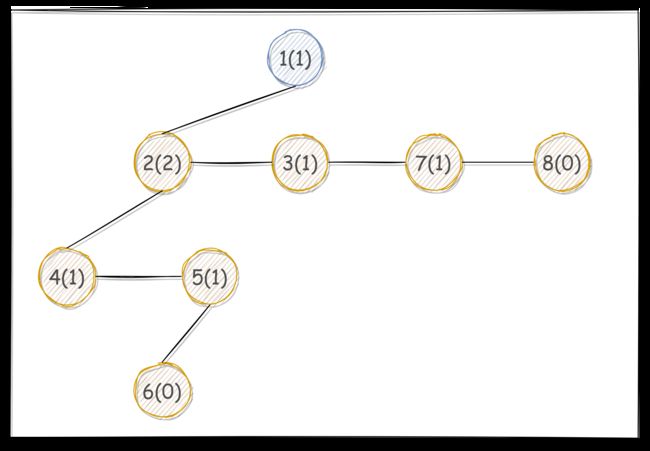
发现树中的结点的度只可能为1或2

默认度为0
有右兄弟，度+1
有左孩子，度+1 
"""
class TNode:
	def __init__(self, data):
		self.data = data
		self.child = None
		self.sibling = None

def countDegree(root: TNode, k):
	k_count = 0   # 符合条件的节点的个数
	
	my_queue = []
	my_queue.append(root)
	
  # 采用BFS的遍历思想
	while len(my_queue) != 0:
		degree_count = 0  # 度个数统计
		node, my_queue = my_queue[0], my_queue[1:]
		if node.child is not None:
			degree_count += 1
			my_queue.append(node.child)

		if node.sibling is not None:
			degree_count += 1
			my_queue.append(node.sibling)

	  # 符合条件的计数
	  k_count += (degree_count == k)

	return k_count

二、 操作系统部分

1、（15 分）简答题。
（1）什么是物理设备和逻辑设备，说明它们之间的关系。
答：物理设备是真实存在的硬件设备，逻辑设备是通过软件模拟出的，没有物理设备不可能存在逻辑设备，但有物理设备不一定有逻辑设备。逻辑设备依赖于物理设备，在程序访问逻辑设备时，需要访问对应的逻辑设备表，其映射到对应的物理设备上。

（2）进程在 CPU 中执行时，操作系统有哪些操作模式，为什么要区分这些操作模式？
答：分为核心态和用户态。当系统需要执行一些高风险操作时（如写文件、中断），需要由系统层面自己完成，防止用户滥用这些操作，危害操作系统甚至硬件。

（3）死锁解除的方法有哪些？请设计应用于手机操作系统的死锁解除方法。
答：死锁的解除包括：1）资源剥夺法； 2）撤销进度法； 3）进程回退法。手机操作系统的死锁解除：可以强制杀死死锁的进程，并释放其占有的所有资源。

2、（15 分）采用动态优先级调度算法（优先数高的优先级低），根据运行时间和等待时间
对优先数进行动态老化，具体老化算法如下：
（a） 处于等待状态的进程优先数 p 根据等待时间进行变化，每毫秒减一；
（b） 处于运行状态的进程优先数 p 根据运行时间进行变化，每毫秒加二；
（c） 优先数相同的进程按以下顺序调度：1）运行中的进程；2）先进入就绪队列的进程；
（d） 优先数 p 每隔 1 毫秒重新计算；
（e） 采用抢占式调度策略。
根据下表给出的 5 个进程的到达时间和执行时间，回答下列问题。（时间单位：毫秒）

进程	执行时间	达到时间	优先级p
P1	2	0	8
P2	2	1	4
P3	3	2	6
P4	1	3	2
P5	2	4	10

（1） 画出 5 个程序执行的甘特图；
（2） 根据以上调度算法，分别计算出每个进程的等待时间和响应时间。

本题和2015年的原题高度相似

3、（15 分）在一个请求分页存储管理系统中，试采用最先进入后淘汰（与 FIFO 相反）和最近使用先淘汰（与 LRU 相反）进行页面置换，假设系统分配给作业的物理磁块个数为 4，访问序列为：4，3，2，1，4，3，2，1，2，1，5，2，1，分别计算采用上述两种置换方法时的缺页次数和缺页率。

本题和2016年的原题高度相似
在本题中，最先进入后淘汰与最近使用先淘汰的调度一致

缺页次数 = 6
缺页率 = 6/13

4、（15 分）假设计算机系统中有同类资源 $a$ 个，由 $b$ 个进程共享该资源，证明在满足下列两个条件的情况下，系统不会发生死锁。
（1） 每个进程所需的最大资源数在 1 和 $a$ 之间；
（2） 所有进程所需的资源数总和小于 $a+b$。

证明：首先更具死锁的定义可知，发生死锁时资源需求量的最大值为$(a-1)b+1$
系统的资源总和$D$：$b<D<ab<a+b$
联立两式：$(a-1)b+1=ab-b+1<a+b-b+1=a+1$
即$(资源需求最大值)<a+1$
等价于$(资源需求最大值)\le a$
所以系统不会发生死锁

5、（15 分）假设当前有一个包含 100 个盘块的文件，其后是若干空闲区。文件控制块不在主存中（索引表也不在主存中），当进行如下操作时，请计算分别采用连续分配、链接分配和单级索引分配策略时各需要多少次磁盘 I/O 操作？
（1） 在文件开头删除一个物理块。
连续分配：读文件控制块一次；修改文件其实位置信息，并写回一次。共2次
链接分配：读文件控制块一次；修改头指针到下一块，并写回一次。共2次
单级索引分配：读文件控制块一次；读索引一次；修改索引并写回。共3次

（2） 在文件中间增加一个物理块并进行写入操作。
中间位置即位第50个物理块的信息
连续分配：读入文件控制块一次；移动50-99位的文件，需要50*2=100次；写入50位的数据一次；修改文件控制块的信息并写回一次。共103次
链接分配：读入文件控制块一次；依次读取0-50块，找到第50块的前驱与50块的后继，需要51次；写入50块如磁盘一次；修改49块的链接一次。共54次
单级索引分配：读入文件控制块与索引两次；写入到磁盘一次；写入索引一次。共4次

（3） 在文件末尾删除一个物理块
连续分配：读入文件控制块一次；修改文件控制块并写回一次。共2次
链接分配：读入文件控制块一次；一次读取0-98块，找到第99块的前驱，需要99次；修改第98块的链接信息并写回一次；共101次
单级索引分配：读入文件控制块和索引两次；修改最后一块所对应的索引信息并写回一次。共3次