最佳适应算法流程图_CVRP问题求解（一）整数编码的粒子群算法

CVRP问题求解（一）整数编码的粒子群算法

粒子群算法概述

粒子群算法(Particle Swarm Optimization)是由鸟群捕食得到启发的一种算法，在鸟类觅食过程中，每只鸟都会利用自身经验和群体信息来寻找食物。在觅食过程中，每只鸟仅仅追踪有限数量的邻居，但是最终整个鸟群好像在某个中心的控制下飞行。这一现象说明复杂的全局行为可以由简单规则的相互作用形成，其表现取决于群体搜索策略和群体之间的信息交换。

PSO基本原理

根据上面现象进行抽象，PSO算法是一种在$n$维搜索空间中(搜索空间可能是解空间，也可能是问题空间，取决于如何对需要求解的问题进行编码)，用由$m$个粒子组成的种群通过一定的搜索策略进行位置更新，从而寻找搜索空间中适应度最佳值的算法。

在这个过程中，每个粒子的位置代表优化问题的一个解(大多数情况下是可行解)。适应度函数是和优化问题的目标函数直接相关的，它通常是针对具体问题进行具体设计，从而帮助算法收敛到最优解。

我们将上面所述的种群记做

，其中第

个粒子的位置为

，速度为

。粒子

的个体最佳适应度值为

，所属邻域的全局最佳适应度为

。

粒子的位置和速度以迭代的方式进行如下更新：

其中各参数说明如下：

• 是粒子
  在第
  步迭代时的速度，
  是
  在第
  维的速度分量；
• 是粒子
  在第
  步迭代的位置，
  是
  第
  维的位置分量；
• 是粒子
  在第
  步迭代时的个体最佳适应度对应位置；
• 是粒子
  在第
  步迭代时的所属邻域最佳适应度对应位置；
• 称为惯性权重，它体现了粒子继承原有速度的多少，在一定范围内，惯性越大，则粒子受原有速度影响越大，受当前环境影响越小，表现为粒子具有更多的发散性，算法的
  全局搜索能力更好；惯性越小，则粒子受到当前环境影响越大，表现为粒子的收敛性强，局部搜索能力更佳；
• 为加速度常数，
  体现了粒子对于自身经验的信任情况，
  体现了粒子对于邻域内其他个体传递信息的信任情况；
• 是[0,1]之间的随机数，服从均匀分布；

需要注意的是速度更新的每一步中，对

的每一个分量都会进行一次取随机数，因此移动的方向并非严格是自身速度、向自身最佳历史位置和向邻域最佳历史位置的组合，而是在一个区域内的近似，如下图所示：

上面的更新方程体现了粒子群算法的一些基本性质：

• 在搜索过程中，粒子有三种方式调整自身的速度：沿着之前的方向；根据自身经验改变方向；根据邻域内其他粒子传递的信息改变方向；而
  三个参数反应了对这三种方式的权重分配；
• 粒子群中的粒子具有一定记忆特性和对环境的感知，这是通过记录自身的最佳适应度对应位置和邻域内粒子的最佳适应度对应位置来实现的，这种个体之间的记忆和信息的交流共享是群体智能算法的重要特性。

基本PSO的改进

基本粒子群的一些问题

标准的粒子群算法存在的主要问题(大部分也是群体进化计算的共性问题)为：

• 初始化过程是随机的，部分粒子位置不佳，在搜索过程中没有有利作用。这样虽然可以保证初始种群的粒子在搜索空间内分布比较均匀，但是由于没有利用问题的先验信息，部分粒子远离最优解所在区域，在一定程度上影响到算法效率和解的质量；
• 在高维复杂问题中，容易陷入“早熟”。也就是由于搜索空间较大，种群在还未找到全局最优解时便已经聚集到一起，从而收敛。早熟的收敛点有可能是局部最优，也有可能是局部最优邻域中的某个点。也就是说，早熟的情况下，算法甚至不能保证收敛到局部最优，这极大影响了算法的实用性；
• 超参数的选定比较困难。例如对于速度的设定，如果速度过大，前期搜索速度会很快，但是容易错过最优解(类似于梯度下降中步长过大的情况)；而速度设定过小则会导致搜索效率低，收敛慢，同样难以应用；

收敛速度改进

对于粒子群算法来说，收敛速度主要由粒子的飞行速度决定，而飞行速度由

三个超参数决定，因此对收敛速度的改进也就集中在对这三个超参数的选择和更新策略上。

对于

，如前所述，较大的

有利于全局搜索，而较小值则对局部搜索有利，

常用的惯性权重值介于0.8与1.2之间。在搜索前期，我们通常需要进行大规模的全局搜索，而在后期则是在最优解邻域内对解进行fine tune，根据这个特点，现在比较常用的

更新策略是线性权值递减策略(Linearly Decreasing Weight, LDW)，即在搜索开始时采用较大的权值，而随着搜索过程进行对权值进行递减，从而满足我们前面说的期望。

线性权值递减的权值更新策略如下：

其中，

为权重初始值，

为权重最终值。

为最大迭代步数，

为当前迭代步数。一个比较常用的默认参数是选择

。采用线性权值递减默认参数，得到的权值变化图如下：

对于加速度常数

来说，通常是对具体问题进行一系列的实验来选取最优值。目前还没有研究结果能在事先给出“最优”的参数选取。一种常用的经验方法是在起始时先让

。

族群多样性改进

对于随机优化算法的性能来说，族群的多样性是非常重要的：

• 为了尽最大可能找到全局最优解，我们总是希望在计算开始时，粒子能够在搜索空间内尽可能均匀发散的分布；而随着计算的进行，粒子逐渐聚集，最终达到收敛；
• 在另一方面，族群多样性会影响到收敛速度，如果族群非常分散，那么其收敛速度通常会比较慢。

对于族群多样性的改进一般有两种方法：改进拓扑结构（也就是粒子之间相互连接的方式）和设计保持种群多样化策略。

拓扑结构的改进

粒子群算法在邻域中共享信息，而邻域是由拓扑结构定义的，因此不同的拓扑结构决定了信息在粒子之间传递的速度。下图展示了一些常见的邻域拓扑结构：

当邻域结构是全连接(Fully connected)时，对于任意粒子来说，整个种群都是它的邻居，这种情况下的PSO也叫做全局版本；当邻域结构是其他拓扑结构时，对于一个粒子，只有在拓扑结构上与其直接相连的粒子才是它的邻居，这种情况下的PSO也叫做局部版本。

除了固定的拓扑结构以外，也有学者提出用动态拓扑结构来改变种群中信息的流动速度；还可以引入聚类的思想，用聚类后的簇中心粒子位置来替代粒子自身最优解位置，用全局的簇中心位置来替代全局最优解位置。

种群多样化策略

在粒子群算法中，随着迭代的进行，种群逐渐收敛到一点，也就丧失了进化的动力，如果收敛时机过早，就会影响到找到的解的质量。为了保持种群的多样性，研究者设计了一系列的策略，下面列出几个比较有名的：

• Clerc提出了no-hope/re-hope策略，在迭代过程中对种群进行no-hope检验，如果发现种群进化动力丧失，就进入re-hope过程，让种群重新在搜索空间中分散开，防止陷入局部最优；
• Xie提出了一种耗散粒子群优化算法，通过施加噪声扰动，为系统引入负熵，从而为种群保留不断进化的动力；
• Thiemo等提出了一种粒子空间扩展策略，为每个粒子赋予一个半径值，以检测是否发生碰撞，当两个粒子发生碰撞时，让它们弹开，以保持种群的多样性；
• ...

融合其他算法思想

单一算法的搜索策略和脱离局部最优的能力是有限的，因此智能算法常常会选择融合其他算法的机制来增加寻优能力。

微分进化思想、遗传算法、多种群协作和竞争思想、混沌搜索、免疫算法和模拟退火等等算法和思想都可以融合进PSO中。

PSO算法流程

标准PSO的流程可以用下面的流程图表示：

---

离散粒子群算法(Discrete PSO)

在求解VRP类问题，或者扩大到离散优化和组合优化问题时，我们首先需要注意PSO的编码问题。

原始的PSO采用实数编码，对于速度计算、位置更新等非常方便而自然，但是对于离散优化和组合优化问题，有时实数编码难以直接应用，这就需要应用二进制编码(Binary encoding)或者排列编码(Permutation encoding)，对于非实数编码，需要重新定义距离、速度、位置的含义和相应操作。

从连续到离散 -- 操作的重定义

粒子群算法中的抽象操作

回顾基本的粒子群算法，在整个搜索过程中，我们涉及的抽象操作有以下几种：

• 粒子的速度计算：位置-位置 -> 速度
• 速度的标量乘：标量*速度 -> 速度
• 速度和：速度+速度 -> 速度
• 粒子的位置更新： 位置+速度 -> 位置

此外还有粒子的评价，但是由于评价涉及到粒子的解码，是具体问题具体设计的，并不具有通用性，因此无法进行抽象层面的定义。

PSO求解VRP问题的排列编码

对于有

个顾客的VRP问题，这里采用排列编码，即粒子的位置

用

到

的整数排列来表示。

例如对一个包含5个顾客的问题来说，一个可能的粒子位置为

。

操作的定义

这里参考Clerc在用PSO求解TSP问题中定义的操作：

粒子速度的定义

对于排列编码，其搜索空间为所有可能的排列。为了进行不同排列的探索，速度定义为对排列的一系列交换。

设

为速度的长度(即交换的次数)，

定义为对

两数进行一次交换，那么速度可以定义为：

一个空的速度定义为

，也就是空集。

定义

，则负速度

可以定义为：

粒子的位置更新

明确了位置和速度的含义之后，就可以很容易的对粒子的位置进行更新了。

假设在某个时刻，一个长度为5的粒子的位置为

，速度为

，那么可以得到：

需要注意的是，对于

，我们可以得到同样的

，这也就是说

和

是等效的。

粒子的速度计算

粒子的速度通过两个位置的差得到，也就是说从两个位置

，我们可以计算出

使得

。如前所述，给定的两个位置并不能得到唯一的速度

，因此我们需要设计一些算法来求得速度。

一个可行的算法是“换位减”，对于有

个顾客的VRP问题，“换位减”的步骤如下：

1. 初始化i=0，v为空集
2. 如果i=N，跳转到步骤4，否则进入步骤3
3. 比较X1和X2，如果在第i个位置上 X1[i] = X2[i]，设定i=i+1，跳转到步骤2；如果 X1[i] != X2[i]，则交换X2中的元素X1[i]和X2[i]，设定i=i+1，将(X1[i],X2[i])加入v，转入步骤2
4. 算法结束，输出速度

下图给出了一个计算过程的示例：

最终我们得到速度

速度的标量积

速度

乘以一个标量

得到的仍然是速度。这里的标量有几种可能性：

• ，此时
  ；
• ，令
  ，从
  中取前
  个分量；即
  ；
• ，那么
  可以拆分为一个不大于
  的整数
  和一个
  之间的小数
  ，即
  ，此时
  ，第二部分的计算同上，第一部分则是对
  的重复 --
  ，也即重复
  次
  ；
• ，则
  ，也就是对常数取负，得到一个正系数，然后乘以负速度；

这样就完整定义了速度的数乘。

速度和

两个速度的和定义为两个速度中交换操作的有顺序的并集。例如

，那么有：

这里需要注意的是

，也就是速度求和并不具备交换性。

时间复杂度分析

对于优化算法来说，时间复杂度是一个重要的问题。如果时间复杂度过高，算法的可扩展性就较差，对于大规模问题很可能不能适用。

假设PSO算法的种群规模为

，迭代次数为

，问题规模为

。我们可以先对单个粒子上的操作进行时间复杂度分析，然后扩展到整个种群。

对于单个粒子，各个操作的复杂度如下：

• 适应度评价：对于VRP问题来说，我们需要对每个个体的路径长度进行加总，其复杂度为
  ；
• 选择个体历史最优和邻域历史最优位置：复杂度为
  ；
• 速度计算：采用换位减的方式，需要对编码从左向右进行一次线性扫描，其平均复杂度为
  ；
• 位置更新：复杂度和速度的长度相关，在最坏情况下速度的长度也不会超过
  ，因此位置更新的复杂度也是
  ；

因此对于单个粒子来说，一次迭代的时间复杂度和问题规模成正比，为

。

可以得到整体算法的复杂度为

。

---

用离散粒子群算法求解CVRP问题

算例介绍

本文采用的CVRP算例来自Augerat et al. 的数据集，可以到这里下载。

下面就数据结构进行说明，任意一个数据文件，例如A-n32-k5，都分为下面几个部分:

数据信息

这部分形如：

NAME : A-n32-k5
COMMENT : (Augerat et al, Min no of trucks: 5, Optimal value: 784)
TYPE : CVRP
DIMENSION : 32
EDGE_WEIGHT_TYPE : EUC_2D 
CAPACITY : 100

给出了数据集的基本信息：

• 数据集名为 A-n32-k5
• 最小用车5辆，最优解路径总长度为784
• 类型是CVRP问题
• 维度，也就是节点数为32
• 边的权重类型为2D的欧几里得距离
• 车辆最大载重为100单位

节点坐标

NODE_COORD_SECTION 
 1 82 76
 2 96 44
 3 50 5
 4 49 8
 ...

给出了节点的编号和X，Y坐标。根据这个信息我们就可以计算两个节点之间的二维欧几里得距离了。

节点需求

DEMAND_SECTION 
1 0 
2 19 
3 21 
4 6 
5 19 
6 7 
...

给出了各个节点的需求量。

车库

DEPOT_SECTION 
 1  
 -1

表明这个问题中只有一个车库，也就是节点1。要求每条路径从车库出发，到车库结束。

代码实现

在这里我们用代码实现一个标准的整数编码PSO，在前面提到的数据集里选择几个进行测试，了解不额外增加局部搜索和脱出局部最优机制的情况下，整数编码PSO的性能表现。

代码作为演示之用，没有经过性能优化，只能作为一个参考。

速度类

对于速度，按照之前所列，我们需要实现标量乘、取反和加法操作，这些可以通过运算符重载做到。

# --------------------------------
# 速度类
# --------------------------------
class Velocity(object):
    """
    整数编码下PSO的速度形如[(1,3), (2,5)]，其含义为先对1, 3节点进行交换，然后对2, 5节点进行交换
    """

    def __init__(self, exchange_list=None):
        if exchange_list is None:
            self._vel = list()  # 私有变量，保存交换对
        else:
            self._vel = exchange_list

    def __mul__(self, c: float):
        """
        重载乘法，允许浮点数 c 和速度 v 相乘
        浮点数c有下面四种情况：
        1. c < 0， 此时对常数取负，得到一个正数，同时对速度也取负，转化为正数和速度的乘法
        2. c = 0，此时得到 cv = empty set
        3. c in (0,1]，此时从v中提取前 int(c * len(v)) 个分量
        4. c > 1，此时可以拆分为一个大于1的数
        :param c: float，一个浮点数
        :return: 处理之后的速度
        """
        # 数据类型检查
        try:
            c = float(c)
        except:
            raise ValueError('Velocity can only be multiplied with a float, not {}'.format(type(c)))
        # 进行乘法
        if c < 0.0:  #
            return -c * (-Velocity(self._vel))
        elif c == 0.0:  # 返回空速度
            return Velocity()
        elif 0 < c <= 1:  # 从前向后取v中的部分分量
            vel_len = len(self._vel)
            cnt = int(c * vel_len)
            return Velocity([self._vel[i] for i in range(cnt)])
        else:  # c > 1的情况，分成整数和小数部分进行处理
            int_part = int(c)  # 整数部分
            dec_part = c - int_part  # 小数部分
            return Velocity(int_part * self._vel) + dec_part * Velocity(self._vel)

    def __rmul__(self, c: float):
        return Velocity(self._vel) * c

    def __neg__(self):
        """
        重载取反操作
        对于Velocity([x,y],[y,z],...)来说， -Velocity = ([y,x],[z,y],...)
        :return:
        """
        return Velocity([[elem[1], elem[0]] for elem in self._vel])

    def __add__(self, other):
        """
        重载速度加法
        对于两个速度 vel1 = [[x,y], [y,z], [z,t]]和 vel2 = [[z, x]]
        vel1 + vel2 = [[x,y], [y,z], [z,t], [z,x]]
        :param other:
        :return:
        """
        return Velocity(self._vel + other.exchange_list)

    def __repr__(self):
        return "Velocity({})".format(str(self._vel))

    @property
    def exchange_list(self):
        """
        Getter函数，取出交换对
        :return:
        """
        return self._vel

位置类

对于位置类，我们需要实现换位减以及和速度相加：

# --------------------------------
# 位置类
# --------------------------------
class Position(object):
    """
    整数编码下的位置类形如[3,2,6,4,5]，它是 *所有节点* 的一个permutation
    """

    def __init__(self, seq=None):
        if seq is None:
            self._seq = list()  # 保存一个permutation，代表路径上访问节点的次序
        else:
            self._seq = seq

    def __sub__(self, other):
        """
        两个Position实例进行 *换位减* ，得到一个Velocity实例
        :param other: Position实例
        :return: Velocity实例
        """
        exchange_list = list()
        if len(self._seq) != len(other.visit_sequence):
            raise Exception("Cant perform calculation for Positions with different sequence length")
        pos2_seq = list(other.visit_sequence)
        for i in range(len(self._seq)):
            elem_seq1 = self._seq[i]
            elem_seq2 = pos2_seq[i]
            if elem_seq1 != elem_seq2:  # 如果两个position对应位置上的元素不相等
                # 找到pos2_seq中这两个元素对应的index
                idx1, idx2 = pos2_seq.index(elem_seq1), pos2_seq.index(elem_seq2)
                # 交换两个元素并将该操作加入velocity
                pos2_seq[idx1], pos2_seq[idx2] = pos2_seq[idx2], pos2_seq[idx1]
                exchange_list.append([elem_seq1, elem_seq2])
        return Velocity(exchange_list)

    def __add__(self, other):
        """
        Position + Velocity = Position
        也即是在permutation上应用Velocity所表示的变换
        例如Position = [1, 3, 2, 4, 5]， Velocity = [[1,3], [2,5], [3,4]]
        Position + Velocity = [4, 1, 5, 3, 2]
        :param other:
        :return: 一个Position实例
        """
        seq_new = list(self._seq)
        for elem in other.exchange_list:
            idx0, idx1 = seq_new.index(elem[0]), seq_new.index(elem[1])
            seq_new[idx0], seq_new[idx1] = seq_new[idx1], seq_new[idx0]
        return Position(seq_new)

    def __repr__(self):
        return "Position({})".format(str(self._seq))

    @property
    def visit_sequence(self):
        return self._seq

粒子类

最终粒子类除了包含一个速度实例和一个位置实例以外，还需要保存个体最佳位置和邻域最佳位置：

# --------------------------------
# 粒子类
# --------------------------------
class Particle(object):
    def __init__(self, position=None, velocity=None):
        if position is None:
            self.pos = Position()
        else:
            self.pos = position  # 当前位置，一个Position实例
        if velocity is None:
            self.vel = Velocity()
        else:
            self.vel = velocity  # 当前速度，一个Velocity实例
        self.fitness = 0.0  # 当前位置对应的适应度
        self.pbest_pos = None  # 个体历史最佳位置，Position实例
        self.pbest_fitness = float('Inf')  # 个体历史最佳适应度
        self.gbest_pos = None  # 邻域最佳位置，Position实例
        self.gbest_fitness = float('Inf')  # 邻域最佳适应度
        self._dimension = utilities.problem_dimension  # 问题维度

    def __repr__(self):
        return "Particle:ntPosition:({})ntVelocity({})ntFitness: {}".format(str(self.pos.visit_sequence),
                                                                                  str(self.vel.exchange_list),
                                                                                  self.fitness)

    def initialize_pos(self) -> None:
        """
        初始化粒子位置
        :return:
        """
        perm = [i for i in range(2, self._dimension + 1)]
        random.shuffle(perm)
        self.pos = Position(perm)

    def __update_velocity(self, omega: float, c1: float, c2: float) -> None:
        """
        根据gbest_pos和pbest_pos更新速度
        :return:
        """
        inertia = omega * (self.pbest_pos - self.pos)
        individual_experience = (c1 * random.random()) * (self.pbest_pos - self.pos)
        social_experience = (c2 * random.random()) * (self.gbest_pos - self.pos)
        self.vel = inertia + individual_experience + social_experience

    def update_pos(self, omega: float, c1: float, c2: float):
        """
        根据速度更新粒子的位置
        :param omega:
        :param c1:
        :param c2:
        :return:
        """
        self.__update_velocity(omega, c1, c2)
        self.pos = self.pos + self.vel

算法性能测试

超参数

作为简单测试，并没有对超参数进行特别调优，按照经验选取超参数如下：

测试结果

这里我选择了4个不同点数的问题进行测试，对每个数据集，运行5次算法，下表中列出了最佳值和平均值，计算gap时使用的是5次平均结果：

结果讨论

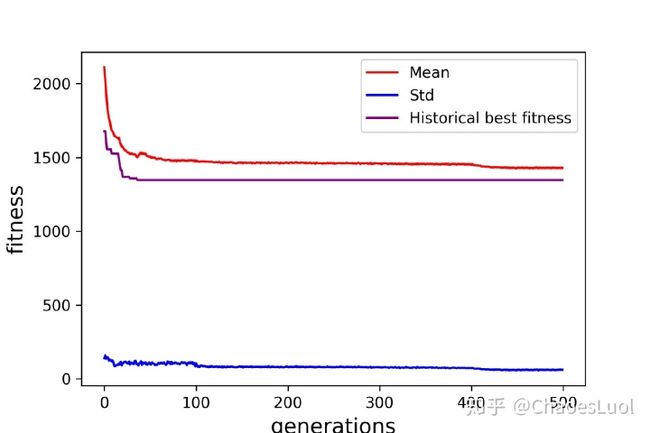
在所有的计算中，算法都已经达到了收敛，对于A-32-k5数据集的一次计算中的迭代过程如下：

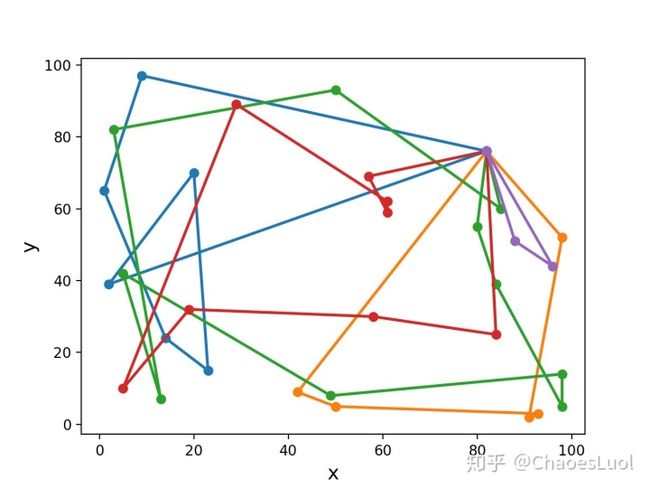
对应的路径图如下：

可以看到，即使对于这样一个节点数比较少的问题，从图像上看得到的路径也和最有路径相去甚远，可以看到不少的路径交叉出现，这也是因为我们没有在算法中加入opt这样的local search机制。

总结

• 整数编码的PSO提供了一套对速度和位置以及其相关运算的定义，拓展了PSO的可用范围，看着还是比较有意思的
• 虽然编码方式比较简单，但是由于定义了一整套的相关运算，其实现还是相对复杂的，而且换位减的时间复杂度也比较高，从效率上并不是非常好的选择
• 仅从编码方式看，也存在一定的问题，例如说[3,2,1,4]和[4,1,2,3]，虽然在定义上是两个不同的位置，但是实际上代表的路径的总距离是相同的(symmetric edge的情况下)；这可能会让解在两个局部最优之间摆动，尽管这两个局部最优实际上是同一回事
• 从结果上看，总体上整数编码的PSO在不添加额外搜索机制的情况下，只能说可以用于求解，但是其相对于最优结果的gap是较大的，也就是说单独这套方法的实用性并不高，甚至比不上一些简单的启发式方法