时序数据学习笔记（十）

一、向量自回归模型（VAR）

        VAR 模型可以看作是AR模型的推广，以允许多个时间序列的预测，VAR模型也要求每个时间序列都是平稳的，其原理是假设两个时间序列的过去值都对另一个时间序列有显著的预测作用。

        VAR模型的使用流程为：先测试数据组内数据的平稳性，如果不平稳使用差异化处理，当数据组内的数据都平稳时；然后对数据组进行AIC排序，获取最有参数组后，再使用granger因果检验判断数据组中的数据是否相互间存在关系。

        如果因果检验为无关系，则此数据无法使用VAR模型进行预测，此时可以转为使用SARIMAX 模型，反之则可使用VAR模型。

        granger 【格兰杰】因果检验（统计检验）：帮助我们验证两个时间序列相互影响的假设，格兰杰因果关系检验仅限于预测因果关系，因为我们只是确定一个时间序列的过去值在预测另一个时间序列时是否具有统计学意义。

二、模型试用

1、选择数据维度

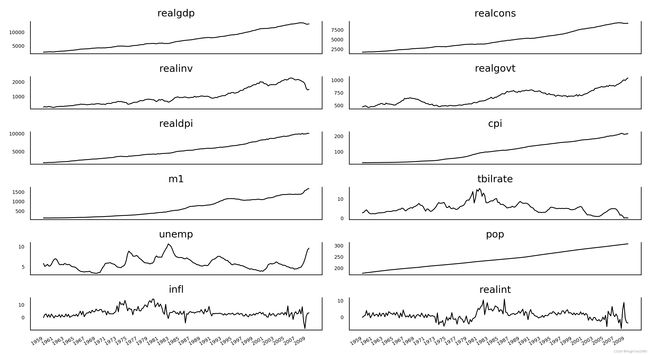
        根据对美国GDP数据各维度趋势图观测，可以发现realdpi与realcons趋势相似，因此此次VAR模型使用这两个维度数据进行；

 2、数据稳定性处理

 a、ADF判断

        两组数据的P值皆大于0.05，因此两组数据都非平稳

ad_fuller_result_1 = adfuller(macro_econ_data['realdpi'])
print(f'ADF Statistic: {ad_fuller_result_1[0]}')
print(f'p-value: {ad_fuller_result_1[1]}')

ad_fuller_result_2 = adfuller(macro_econ_data['realcons'])
print(f'ADF Statistic: {ad_fuller_result_2[0]}')
print(f'p-value: {ad_fuller_result_2[1]}')

realdpi ADF Statistic: 2.9860253519546873
realdpi p-value: 1.0
realcons ADF Statistic: 1.5499123380509545
realcons p-value: 0.9976992503412904

 b、差异化处理

        经过差异化处理后，数据呈平稳性，可以进行下一步P阶值查找；

ad_fuller_result_1 = adfuller(macro_econ_data['realdpi'].diff()[1:])
print(f'ADF Statistic: {ad_fuller_result_1[0]}')
print(f'p-value: {ad_fuller_result_1[1]}')

ad_fuller_result_2 = adfuller(macro_econ_data['realcons'].diff()[1:])
print(f'ADF Statistic: {ad_fuller_result_2[0]}')
print(f'p-value: {ad_fuller_result_2[1]}')

realdpi  ADF Statistic: -8.864893340673008
realdpi  p-value: 1.4493606159108096e-14
realcons ADF Statistic: -4.204306080845245
realcons p-value: 0.0006479282158627595

3、P阶参数值查找

a、训练与测试数据集拆分

endog_diff = macro_econ_data[['realdpi', 'realcons']].diff()[1:]
train = endog_diff[:162]
test = endog_diff[162:]

 b、AIC排序选择参数

        通过AIC排序得出p=3时最佳；

def optimize_VAR(endog: Union[pd.Series, list]) -> pd.DataFrame:
    results = []
    for i in tqdm_notebook(range(15)):
        try:
            model = VARMAX(endog, order=(i, 0)).fit(dips=False)
        except:
            continue
        aic = model.aic
        results.append([i, aic])
    result_df = pd.DataFrame(results)
    result_df.columns = ['p', 'AIC']
    result_df = result_df.sort_values(by='AIC', ascending=True).reset_index(drop=True)
    return result_df

result_df = optimize_VAR(train)
print(result_df)

     p          AIC
0    3  3123.070078
1    5  3123.708523
2    6  3126.855598
3    4  3129.194046
4    2  3130.091668
5    7  3133.395731

4、granger因果效验

        通过因果效验发现p值皆小于0.05，表示realdpi与realcons直接存在联系，满足VAR模型使用的基本要求；

granger_1 = grangercausalitytests(macro_econ_data[['realdpi', 'realcons']].diff()[1:], [3])
granger_2 = grangercausalitytests(macro_econ_data[['realcons', 'realdpi']].diff()[1:], [3])

 realdpi=>realcons

ssr based F test:         F=9.2363  , p=0.0000  , df_denom=192, df_num=3
ssr based chi2 test:   chi2=28.7191 , p=0.0000  , df=3
likelihood ratio test: chi2=26.8268 , p=0.0000  , df=3
parameter F test:         F=9.2363  , p=0.0000  , df_denom=192, df_num=3

 realcons=>realdpi

ssr based F test:         F=2.8181  , p=0.0403  , df_denom=192, df_num=3
ssr based chi2 test:   chi2=8.7625  , p=0.0326  , df=3
likelihood ratio test: chi2=8.5751  , p=0.0355  , df=3
parameter F test:         F=2.8181  , p=0.0403  , df_denom=192, df_num=3

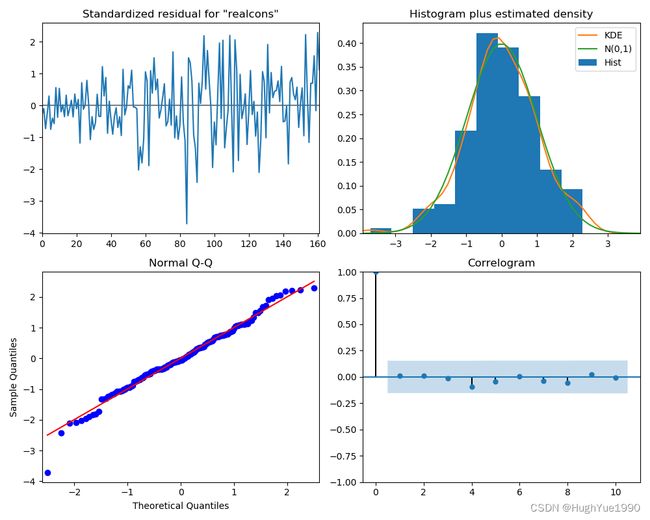
5、 残差分析

        通过对realdpi与realcons进行p阶为3时的残差分析，可以发现分布图、Q-Q图以及相关图可以发现当前模型的残差类似于白噪声，同时由于p-value值全大于0.05，因此此参数组所创建模型可用于预测。

best_model = VARMAX(train, order=(3,0))
best_model_fit = best_model.fit(disp=False)

# realdpi
best_model_fit.plot_diagnostics(figsize=(10,8), variable=0)
plt.show()

# realcons
best_model_fit.plot_diagnostics(figsize=(10,8), variable=1)
plt.show()

realgdp_residuals = best_model_fit.resid['realdpi']

lbvalue, pvalue = acorr_ljungbox(realgdp_residuals, np.arange(1, 11, 1))

print(pvalue)

realcons_residuals = best_model_fit.resid['realcons']

lbvalue, pvalue = acorr_ljungbox(realcons_residuals, np.arange(1, 11, 1))

print(pvalue)

 

realdpi：

 [0.91418526 0.98543475 0.99457788 0.98424553 0.10350634 0.16448105
 0.23382908 0.21259232 0.14872292 0.12192127]
realcons：

[0.87704179 0.96628367 0.99531106 0.99358154 0.99592098 0.99240806
 0.99457689 0.97604149 0.98252209 0.99168092]

6、数据预测

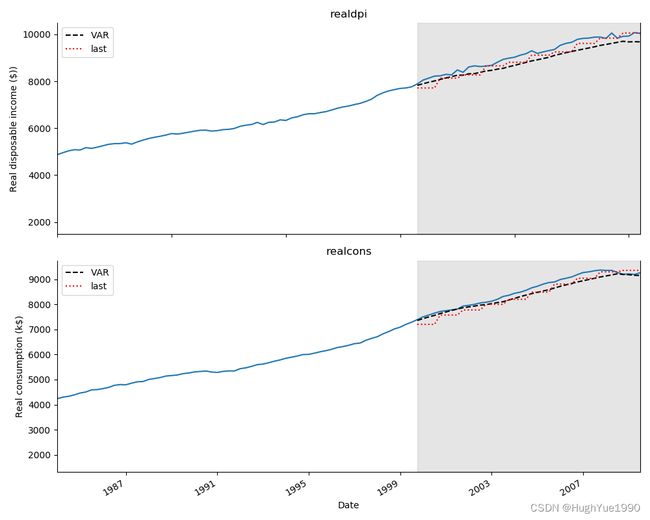
        由于数据采集为每季度一采集，因此时间窗口WINDOW设置为4，并使用VAR预测结果与最后值预测的基线进行比对；

TRAIN_LEN = len(train)
HORIZON = len(test)
WINDOW = 4
realdpi_pred_VAR, realcons_pred_VAR = rolling_forecast(endog_diff, TRAIN_LEN, HORIZON, WINDOW, 'VAR')
test = endog[163:]
test['realdpi_pred_VAR'] = pd.Series()
test['realdpi_pred_VAR'] = endog.iloc[162]['realdpi'] + np.cumsum(realdpi_pred_VAR)
test['realcons_pred_VAR'] = pd.Series()
test['realcons_pred_VAR'] = endog.iloc[162]['realcons'] + np.cumsum(realcons_pred_VAR)
realdpi_pred_last, realcons_pred_last = rolling_forecast(endog, TRAIN_LEN, HORIZON, WINDOW, 'last')
test['realdpi_pred_last'] = realdpi_pred_last
test['realcons_pred_last'] = realcons_pred_last

         通过MAPE结果对比，发现VAR模型在realcons上的预测效果比基线好，但是在realdpi上的预测效果却不如基线；

mape_realdpi_VAR = mape(test['realdpi'], test['realdpi_pred_VAR'])
mape_realdpi_last = mape(test['realdpi'], test['realdpi_pred_last'])
print(mape_realdpi_VAR)
print(mape_realdpi_last)
mape_realcons_VAR = mape(test['realcons'], test['realcons_pred_VAR'])
mape_realcons_last = mape(test['realcons'], test['realcons_pred_last'])
print(mape_realcons_VAR)
print(mape_realcons_last)

mape_realdpi_VAR：3.1384843967028937
mape_realdpi_last：2.2626174331286664
mape_realcons_VAR：1.7712005655316776
mape_realcons_last：2.4593150211915074

完整代码地址：https://download.csdn.net/download/HughYue1990/86725067