时序数据表示学习
- 时序数据表示学习研究背景及工作概述
时序数据在我们的日常生活中广泛存在,随着采集设备不断升级,各类传感器的大规模部署,每天都在以数以亿计的速度产生时序数据。
主要包括遥感领域的GPS轨迹数据,包括卫星通讯,态势监控,雷达遥感,以及其他领域的设备日志,操作记录,用户活动等等。
这类数据具有数据体量庞大,关联信息异构,分析任务多样等特点
对于时序数据的处理框架主要聚焦在存储和索引上,而传统的分析算法难以适应大规模、异构、复杂的分析任务
在2012年斯坦福的教授第一次将深度学习框架引入了时序数据建模上。从而开启了时序数据表示学习的研究。
Deep learning for time series modeling. Busseti Enzo,Osband Ian,Wong Scott(2012)
时序数据表示学习的核心目标是,将时序数据表示为固定长度向量,探索基于表示向量时序数据管理和挖掘新范式。
时序数据表示学习的优势在于:
效率:将时间序列表示为固定长度向量,可以降低时序数据存储及检索响应时间
语义表示:多类数据在同一个隐空间中表示,表达语义信息,从而更好地服务于下游任务
预训练:时序数据表示微调后用于下游任务
目前时序数据表示学习的框架主要分为两个部分。
第一部分是时序数据建模,通过一个时序数据编码器,将数据表示为固定长度的向量。
第二个部分是定义表示学习损失,比如说使用标签信息,对相似性或者自相似性
然而这个过程会存在以下几点挑战
- 各个序列的特点不同,就会存在多序列间关系难建模的问题
- 序列长度长短不一致
- 采样时间间隔不一致
这样的话就要采取不同应用场景下的时序数据编码器。
而在表示学习阶段,我们常常遇到的问题还有以下几个方面。
- 没有足够的监督信息可以用
- 分析任务监督信息弱
- 分析结果可解释性差
对于以上的挑战,我们做了一系列的表示学习模型的工作,尝试去解决这些挑战:
没有足够的监督信息可以用——无监督下时序数据表示学习
分析任务监督信息弱——弱监督下时序数据表示学习
分析结果可解释性差——时序数据归因及因果发现
下面将主要围绕表示模型训练的部分,分模块展示每个挑战下的工作
- 无监督表示学习
2.1. 基于度量学习的轨迹相似度计算
轨迹数据相似度计算复杂度高,通过度量学习(meric leaning) 学习轨迹数据表示降低计算复杂度,达到快速、准确计算轨迹数据相似度的目的。主要的研究思路是,利用部分序列相似度的值作为监督信息,训练表示模型,逼近度量空间
第一篇文章主要是基于记忆网络,提出了一种空间注意力记忆机制(Spatial
Attention Memory,SAM)来建模轨迹之间相似度具有空间近邻的特性
Computing Trajectory Similarity in Linear Time: A Generic Seed-Guided Neural Metric Learning ApproachYao D.,Cong G.,Zhang C…et al.2019 IEEE 35th International Conference on Data Engineering (ICDE)(2019)
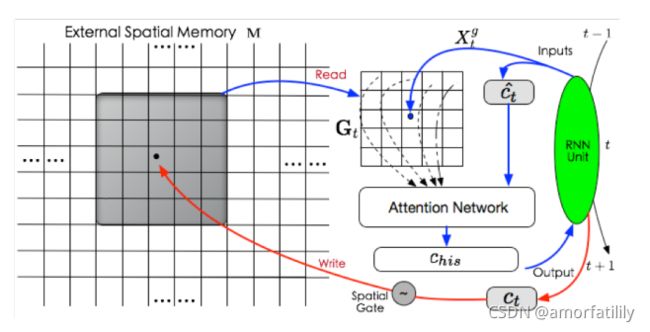
空间注意力机制
第二篇文章在上一篇文章的基础上,提出了加权排序损失(weighted ranking loss),用于为更有区分度的轨迹分配更大的权重。解决了模型收敛慢的问题
A Linear Time Approach to Computing Time Series Similarity based on Deep Metric LearningYao D.,Cong G.,Zhang C…et al.IEEE Transactions on Knowledge and Data Engineering
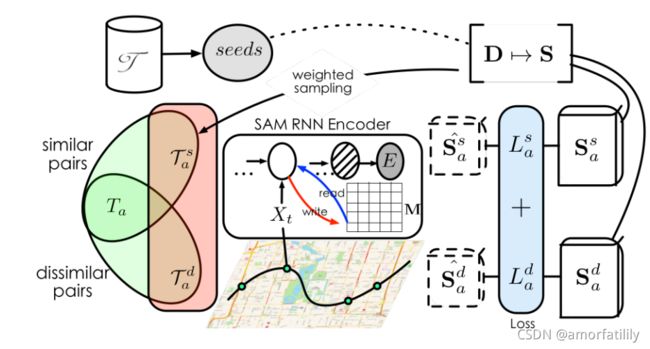
加入加权排序损失
2.2. 路网约束下的轨迹相似性计算
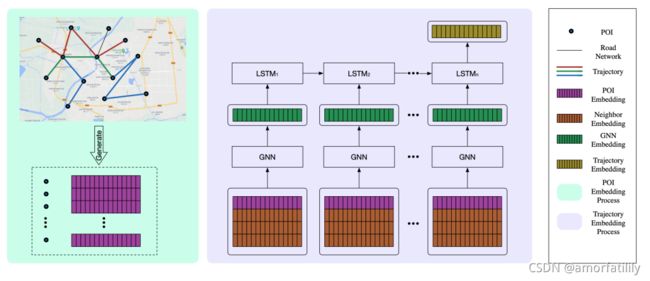
在实际应用中,移动目标的轨迹常常受路网约束,计算轨迹相似度需要考虑路网拓扑结构。本文就是在路网约束下来计算轨迹相似度,不仅需要建模路网的拓扑结构,还需要建模路径在轨迹中出现的频繁程度。
思路是分为两个阶段,首先学习路网中POI(路网交汇点)的表示,利用
GNN和LSTM分别建模路网拓扑结构和序列特征,得到轨迹编码模型。
A Graph-based Approach for Trajectory Similarity Computation in Spatial Networks Peng Han, Jin Wang, Di Yao, Shuo Shang , Xiangliang Zhang.
ACM SIGKDD Conference on Knowledge Discovery and Data Mining (KDD) 2021
模型示意图
2.3 长轨迹下轨迹相似性计算
现有表示学习模型在长轨迹和短轨迹上的准确率差异,经评估在长轨迹上的检索准确率比短轨迹低50%,且长序列用RNN建模效率较低;主要原因在于长时序列数据喂入模型后会有遗忘问题。
目前这个工作还正在开展中,如果有兴趣的老师和同学可以联系姚迪老师沟通
- 弱监督表示学习
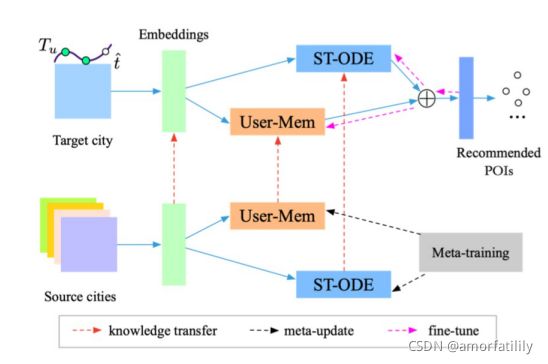
3.1 元学习增强的跨城市轨迹预测
POI推荐是建设智慧城市的基本问题,对城市交通规划,城市商业
布局和环境政策制定等任务非常有用。 由于数据收集机制,通常会导致不同城市的POI轨迹数据分布极度不平衡。 例如,某些城市可能会发布多年的用户POI轨迹数据,而另一些城市则只会发布几天的数据,可利用数据稀少。
另外也存在人类活动的复杂性,导致用户偏好难以建模,以及不同的POI分布和城市结构的因素,导致难以学习跨城市的轨迹预测
本文引入元学习(meta-learning)的方法,提出基于元学习增强的神经常微分方程的POI推荐方法
模型示意图
Meta-Learning Enhanced Neural ODE for Citywide Next POI RecommendationTan H.,Yao D.,Huang T…et al.22nd IEEE International Conference on Mobile Data Management (MDM(2021)
3.2 弱监督下的轨迹异常检测
弱监督主要是指:监督标签少,数据不充足;混杂异常数据,数据监督信息不确定;监督信息不完备等。我们是希望通过提出一个统一的架构使得上述提到的三个问题都得到解决
对于监督信息不足的问题,主要考虑用生成模型的思路,利用充足的无标签轨迹,学习生成式轨迹行为特征表示。
对于监督信息不确定的问题,考虑自监督地学习轨迹样本权重学习,识别无标签轨迹中的疑似异常轨迹
对于监督信息不完备的问题,结合轨迹表示和标签隐含关系,识别未知类型异常轨迹
该工作正在进行中。
- 未来研究规划
主要分为应用研究和理论研究两个方向。
4.1 应用研究方向
面向不同场景的时序数据相似度计算
跨模态时序数据的相似性检索
子轨迹相似性计算
…
弱监督下时序数据异常检测
少样本下的时序数据异常检测
标签信息有误下的异常检测
时序数据类型异常发现
…
4.2 理论研究
面向时序数据分析的可解释机器学习
时序数据归因分析
基于时序数据的因果关系发现
面向时序数据的深度学习油画
…
参考资料 (4)
[1] Busseti Enzo, Osband Ian, Wong Scott. Deep learning for time series modeling. Technical report, Stanford University, 2012: 1–5
[2] Yao D., Cong G., Zhang C., et al. Computing Trajectory Similarity in Linear Time: A Generic Seed-Guided Neural Metric Learning Approach. 2019 IEEE 35th International Conference on Data Engineering (ICDE, 2019: 1358–1369,
[3] Yao D., Cong G., Zhang C., et al. A Linear Time Approach to Computing Time Series Similarity based on Deep Metric Learning. IEEE Transactions on Knowledge and Data Engineering
[4] Tan H., Yao D., Huang T., et al. Meta-Learning Enhanced Neural ODE for Citywide Next POI Recommendation. 22nd IEEE International Conference on Mobile Data Management (MDM, 2021: 89–98,