数学建模美赛模拟题----蜜蜂种群模型、各种因素影响，以及所需活动范围

这是英文版的原题

这其实是2022年美国高中生数学建模竞赛的A题，这次是我们学校选拔赛的测试题。

 这是汉化版的题目

首先，我们提取一下题目的参考文献中的关键信息：

一些养蜂人损失了30%到90%的蜂箱，提出了多种可能的原因:新烟碱或新农药，害虫，如寄生螨瓦氏螨，真菌和细菌或病毒感染，环境压力，营养不良，低遗传多样性，栖息地破坏或气候变化的影响，等等。
蜜蜂通常在1到6公里的范围内飞行，但有时会飞到13.5公里。事实上，有些蜜蜂会飞到离蜂巢20公里远的地方。
所有蜜蜂只有在天气理想的时候才会移动到更远的范围。它们在华氏65度（18℃）左右就能完成觅食活动——蜜蜂也是如此。 
在冬天，它们需要至少55华氏度（13℃）的温度来保持觅食的活跃。随着花朵的减少，蜜蜂会为了节省能量而成为家门口的觅食者。 
蜜蜂可以飞到8公里远的地方去寻找合适的水源，它们每天带着几乎一加仑的水回到蜂巢。 
在炎热的日子里，蜜蜂更专注于获取水分，而不是花粉和花蜜，直到天气适合授粉。 
使用含有新烟碱的杀虫剂往往会抑制蜜蜂的自然行为和飞行模式。这也极大地影响了它们觅食花粉、花蜜和水的能力。 
磁场和辐射会对蜜蜂造成伤害。它们干扰了蜜蜂的自然罗盘，使它们难以精确和安全地飞行。
当条件不太有利时，它们的飞行距离就会缩短。这可能是因为天气、食物的可获得性和人类活动，比如电磁脉冲和辐射

第一问：

        我们需要建立一个模型来确定蜜蜂的种群随时间的变化趋势；

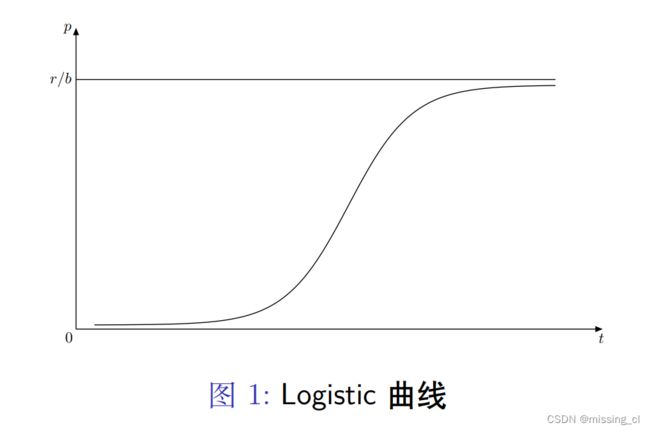
        由于该种群是一个单种群，所以我们优先考虑Logistic模型来对其进行分析：

       

        那么我们就需要定义出生率：

        根据相关论文我们可以了解到，蜜蜂种群的出生率就是他的产卵率，我们从相关论文得到的数据为种群数量为10000左右的蜜蜂种群得到的产卵量，产卵率随温度变化比较大。所以我们寻找了产卵率随温度变化的模型，并将其量化为具体的数值。这样我们就可以根据温度得到每天的产卵率，再根据具体的种群数量得到每天具体的产卵量。我们通过拟合数据得到一下函数，通过时间t得到对应的产卵量：

int eag(int t)
{
	double e = -0.0135 * pow(t, 4) + 1.2839 * pow(t, 3) - 45.909 * pow(t, 2) + 736.75 * t - 4316.3;
	if (e < 0)return 0;
	return e;
}

        我们还需要定义死亡率：

        由于蜜蜂在花季工作强度较大，工蜂的寿命会得到大幅度减少，其寿命只有20-30天，在花粉较少的季节，工蜂的工作强度大大减少，其寿命可达2-3个月。因此我们需要定义一个工作强度和死亡之间的关系，工作强度是与花粉量和飞行的距离相关的。我们从相关论文得到花粉的量随月份的变化，以及气温对蜜蜂飞行距离的影响，并将其量化出来，以最大值为100，将其对应值进行折算得到对应的值。

花粉浓度随季节变化：

蜜蜂飞行距离随温度变化：

        得到的结果为（0℃，40℃）：

 {0 , 0 , 0 , 0 , 0 , 0 , 0 , 0 , 0 , 0 , 0 , 0 , 0 , 1 , 2 , 3 , 4 , 6 , 9 , 14 , 21 , 31 , 46 , 68 , 100 , 74 , 57 , 45 , 36 , 28 , 23 , 18 , 15 , 12 , 10 , 8 , 7 , 6 , 5 , 4 }

        则蜜蜂的工作强度为：花粉浓度×飞行距离

        在这里我们为了保证数据的合理性，我们认为蜜蜂一天的工作强度不超过5，所以我们在其前面乘上一个系数A（随当地气候和环境变化）。

        随后我们判定蜜蜂的死亡条件为：蜜蜂的生存时间+他的工作强度>=120。

        其中死亡还分为“工作死亡”和“夭折”，蜜蜂一生一共有四个阶段，分别为：卵，幼虫，蛹和成蜂。

        这个“工作死亡”发生在成蜂阶段，“夭折”发生在卵这个阶段。

        所谓“夭折”，其实就是卵没有成功孵化为幼虫。这样我们需要得到的就是孵化率，通过相关论文我们得到了其孵化率随温度的变化趋势。

        由于孵化率在后续计算过程中十分不便，所以我们是通过未孵化率（也就是1-孵化率）得到的结果，并把其量化为（其中t的转化为外界温度转化为蜂巢温度）：

double dead_rate(int t)
{
	int t1 = (t - 14) / 3 + 31;
	if (t1 == 31)return 51.5;
	else if (t1 == 32)return 2.5;
	else if (t1 == 33)return 2.1;
	else if (t1 == 34)return 0;
	else if (t1 == 35)return 0;
	else if (t1 == 36)return 6.8;
	else if (t1 == 37)return 5.7;
	else if (t1 == 38)return 12.5;
	else return 100;
}

        于是，我们得到了死亡率的模型。

        最后，我们选取了福建地区比较适合养蜂的地方的气温进行测试：

         我们通过一个结构体来实现（数据有些许改变）：

struct month_wearher
{
	int low = 0;
	int high = 0;
	int max = 0;
	int min = 0;
};

month_wearher wea[13];
	wea[1].low = 12, wea[1].high = 20, wea[1].max = 25, wea[1].min = 3;
	wea[2].low = 13, wea[2].high = 20, wea[2].max = 25, wea[2].min = 1;
	wea[3].low = 16, wea[3].high = 21, wea[3].max = 27, wea[3].min = 6;
	wea[4].low = 22, wea[4].high = 22, wea[4].max = 32, wea[4].min = 9;
	wea[5].low = 24, wea[5].high = 28, wea[5].max = 37, wea[5].min = 16;
	wea[6].low = 28, wea[6].high = 29, wea[6].max = 38, wea[6].min = 19;
	wea[7].low = 30, wea[7].high = 32, wea[7].max = 39, wea[7].min = 24;
	wea[8].low = 30, wea[8].high = 36, wea[8].max = 37, wea[8].min = 22;
	wea[9].low = 28, wea[9].high = 30, wea[9].max = 38, wea[9].min = 19;
	wea[10].low = 23, wea[10].high = 25, wea[10].max = 36, wea[10].min = 0;
	wea[11].low = 15, wea[11].high = 25, wea[11].max = 30, wea[11].min = 10;
	wea[12].low = 10, wea[12].high = 25, wea[12].max = 28, wea[12].min = 5;

        对于每天的温度我们通过随机数来实现，首先产生一个随机数判断是否产生极端天气，我们认为正常天气产生的概率为95%，机断天气发生的概率为5%。我们让这个随机数与39取模，若模为0则产生极端低温，若为39则产生极端高温，其他则在平均最高温和平均最低温里生成一个随机数实现产生当天的温度。

于是我们的代码就实现了：

#include 
#include 
#include 
#include 
#include 
using namespace std;
struct Bee
{
	float workforce = 0;//工作总强度；
	short type = -1;//蜜蜂类型，0-卵，1-幼虫，2-蛹，3-成蜂
	short days = 0;//蜜蜂生存时间
};
int tem[366];//每天对应的温度

void changetype(Bee &x)
{
	if (x.type == -1)return;
	if (x.workforce + x.days >= 120)
	{
		x.days = 0;
		x.type = -1;
		x.workforce = 0;
		return;
	}
	if (x.days > 20)x.type = 3;
	else if (x.days > 6 && x.days<=20)x.type = 2;
	else if (x.days > 3 && x.days <= 6) x.type = 1;
	else if (x.days >= 0 && x.days <= 3)x.type = 0;
}

double dead_rate(int t)
{
	int t1 = (t - 14) / 3 + 31;
	if (t1 == 31)return 51.5;
	else if (t1 == 32)return 2.5;
	else if (t1 == 33)return 2.1;
	else if (t1 == 34)return 0;
	else if (t1 == 35)return 0;
	else if (t1 == 36)return 6.8;
	else if (t1 == 37)return 5.7;
	else if (t1 == 38)return 12.5;
	else return 100;
}


int eag(int t)
{
	double e = -0.0135 * pow(t, 4) + 1.2839 * pow(t, 3) - 45.909 * pow(t, 2) + 736.75 * t - 4316.3;
	if (e < 0)return 0;
	return 4*e;
}
struct month_wearher
{
	int low = 0;
	int high = 0;
	int max = 0;
	int min = 0;
};

void update(Bee mifeng[],int t,int huafen[],int round[],int month,int &s0,int &i0,int &i1,int &i2,int &i3)
{
	i0 = 0, i1 = 0, i2 = 0, i3 = 0,s0 = 0;
	int a = eag(t);
	int l3 = 0;
	int add = 0;
	if (a > 0)
	{
		for (int i = 0; i < 100000; i++)
		{
			if (mifeng[i].type == -1)
			{
				mifeng[i].type = 0;
				mifeng[i].days = 0;
				mifeng[i].workforce = 0;
				add++;
				if (add >= a)break;
			}
		}
	}
	for (int i = 0; i < 100000; i++)
	{
		if (mifeng[i].type != -1)mifeng[i].days++;
		changetype(mifeng[i]);
		if (mifeng[i].days == 3)l3++;
		if (mifeng[i].type == 3)
		{
			mifeng[i].workforce += (float)(huafen[month]*round[t])/2000;
		}
	}
	int d = (l3 * dead_rate(t)) / 100,m =0;
	if (d > 0)
	{
		for (int i = 0; i < 100000; i++)
		{
			if (mifeng[i].days == 3)
			{
				mifeng[i].type = -1;
				mifeng[i].days = 0;
				mifeng[i].workforce = 0;
				m++;
				if (m >= d)break;
			}
		}
	}
	for (int i = 0; i < 100000; i++)
	{
		if (mifeng[i].type == 0)i0++;
		else if (mifeng[i].type == 1)i1++;
		else if (mifeng[i].type == 2)
		{
			i2++;
			
		}
		else if (mifeng[i].type == 3)i3++;
	}
	s0 = i0 + i1 + i2 + i3;
	cout << "剩余" << s0 << "只蜜蜂" << endl;
	cout << "其中：" << endl;
	cout << "剩余" << i0 << "个卵" << endl;
	cout << "剩余" << i1 << "只幼虫" << endl;
	cout << "剩余" << i2 << "只蛹" << endl;
	cout << "剩余" << i3 << "只成蜂" << endl;
}

int main()
{
	srand((unsigned int)time(NULL));
	Bee mifeng[100000];
	int i0 , i1 , i2 , i3 ,s0;
	cout << "请分别输入4个各阶段蜜蜂（卵，幼虫，蛹，成峰）的数量(总数在50000以内)：" << endl;
	cin >> i0 >> i1 >> i2 >> i3;
	s0 = i0 + i1 + i2 + i3;
	for (int i = 0; i < i0; i++) {
		mifeng[i].type = 0;
		mifeng[i].days = rand() % 4;
		mifeng[i].workforce = 0;
	}
	for (int i = i0; i < i0+i1; i++) {
		mifeng[i].type = 1;
		mifeng[i].days = rand() % 3 + 4;
		mifeng[i].workforce = 0;
	}
	for (int i = i0+i1; i < s0-i3; i++) {
		mifeng[i].type = 2;
		mifeng[i].days = rand() % 14 + 7;
		mifeng[i].workforce = 0;
	}
	for (int i = s0 - i3; i < s0; i++) {
		mifeng[i].type = 3;
		mifeng[i].days = rand() % 41 + 20;
		mifeng[i].workforce = rand()%100;
	}
	month_wearher wea[13];
	wea[1].low = 12, wea[1].high = 20, wea[1].max = 25, wea[1].min = 3;
	wea[2].low = 13, wea[2].high = 20, wea[2].max = 25, wea[2].min = 1;
	wea[3].low = 16, wea[3].high = 21, wea[3].max = 27, wea[3].min = 6;
	wea[4].low = 22, wea[4].high = 22, wea[4].max = 32, wea[4].min = 9;
	wea[5].low = 24, wea[5].high = 28, wea[5].max = 37, wea[5].min = 16;
	wea[6].low = 28, wea[6].high = 29, wea[6].max = 38, wea[6].min = 19;
	wea[7].low = 30, wea[7].high = 32, wea[7].max = 39, wea[7].min = 24;
	wea[8].low = 30, wea[8].high = 36, wea[8].max = 37, wea[8].min = 22;
	wea[9].low = 28, wea[9].high = 30, wea[9].max = 38, wea[9].min = 19;
	wea[10].low = 23, wea[10].high = 25, wea[10].max = 36, wea[10].min = 0;
	wea[11].low = 15, wea[11].high = 25, wea[11].max = 30, wea[11].min = 10;
	wea[12].low = 10, wea[12].high = 25, wea[12].max = 28, wea[12].min = 5;
	int mon_day[13] = { 0,31,28,31,30,31,30,31,31,30,31,30,31 };
	int huafen[13] = {0,4,5,21,76,100,74,57,31,35,25,23,11 };
	int round[40] = {0,0,0,0,0,0,0,0,0,0,0,0,0,1,2,3,4,6,9,14,21,31,46,68,100,74,57,45,36,28,23,18,15,12,10,8,7,6,5,4};
	ofstream ouF("data new.txt", ios::out);
	int tian = 0;
	for (int month = 1; month <= 12; month++)
	{
		for (int day = 1; day <= mon_day[month]; day++)
		{
			tian++;
			int t;
			if (rand() % 40 == 0)t = rand() % (wea[month].low - wea[month].min + 1) + wea[month].min;
			else if (rand() % 40 == 39)t = rand() % (wea[month].max - wea[month].high + 1) + wea[month].high;
			else t = rand() % (wea[month].high - wea[month].low + 1) + wea[month].low;
			printf("今天是%d月%d日，当天气温为%d℃，当日产卵%d个\n",month,day,t,eag(t));
			update(mifeng,t,huafen,round,month,s0,i0,i1,i2,i3);
			ouF << tian << " " << t <<" " << s0 << " " << " " << i0 << " " << i1 << " " << i2 << " " << i3 << endl;
		}
	}
	ouF.close();
	return 0;
}

        将数据保存至文件中后，我们通过Python进行绘图:

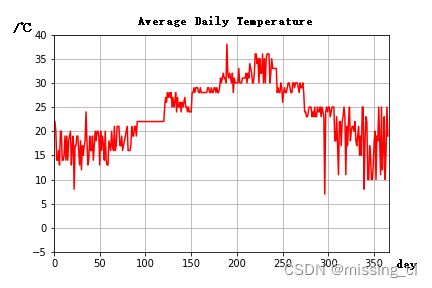
        其中温度变化为：

 

与相关论文得到的模型拟合度较高：

我们的蜜蜂种群模型就得到建立（虽然温度变化有些不合理的地方）！

第二问：

        我们需要讨论相关的环境因素对蜜蜂种群变化的影响：

        我们一共做了4种因素的对比，分别为：温度变化，产卵率变化，寿命变化，年龄结构变化

温度变化：

        我们只需要将当地的温度进行适当变化即可，为了保证实验的公平性，我们只小幅度的改变温度（调高或调低均不超过5℃）。这里，我们测试的是调低5℃组（-5℃）、调低3℃组（-3℃）、正常组（0℃）、调高3℃组（+3℃）、调高5℃组（+5℃），其结果如下：

        我们可以看到：温度对我们这个模型的影响是非常大的。

        对于其解释：+5℃组，由于在冬季温度比之前高，产卵率大大提升，而冬季花粉浓度低，工作强度并不高，所以冬季种群数量会猛增。 

产卵率变化：

        我们只需要将产卵率进行适当变化即可，为了保证实验的公平性，我们只小幅度的改变产卵率（调高或调低均不超过20%）。这里，我们测试的是调低20%组（-20%）、调低10%组（-10%）、正常组（0）、调高10%组（+10%）、调高20%组（+20%），其结果如下：

        我们可以看到：产卵率由于直接影响卵的产生，可以很大程度上影响蜜蜂种群数量的变化。 

寿命变化：

         我们只需要改变蜜蜂的死亡判断条件即可：我们分别测试了寿命为100，110，120，130，140对于的数据，并将其图像绘制处理进行对比。

         我们可以看到：寿命可以让蜜蜂活的更久，干更多的活，在一定程度上能够影响蜜蜂的种群变化。

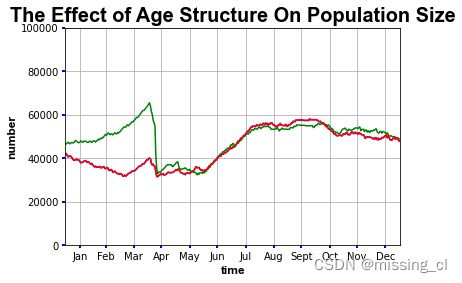
年龄结构变化：

        年龄结构分为：增长型、稳定性和衰退型，在这里我们对2个极端的类型进行分析，也就是对增长型和衰退型进行分析，更能对比得到结论。我们将增长型的四个阶段的比值设置为72：13：9：6，衰退型四个阶段的比值设置为6：9：13：72。结果如下：

        我们可以看到：年龄结构对蜜蜂的种群种群数量影响并不大，增长型在初期，能够快速增长，但由于环境因素的限制，最后与衰退型的变化趋势几乎一致。

        结论：因素影响  温度>产卵率>寿命>年龄结构。

第三问：

        我们需要分析出蜜蜂的种群分布趋势，并求解出该模型在20英亩（81000平方米）的养蜂厂需要多少个蜂群，能够使利益最大化。

        那我们就需要对蜜蜂的飞行距离进行量化得到。

        根据文中信息，蜜蜂的飞行距离一般在1-6KM，而我们第一问所建立的模型存在0-100的变化，那么我们就让蜜蜂的平均飞行距离与之线性对应，得到每一天 的平均飞行距离后。我们的模型认为95%的蜜蜂会在这个平均飞行距离的±15%内变化，5%的蜜蜂会超出15%，根据第一问的思想，我们得出了模型。

        我们对一年365天，每天取100只蜜蜂的样本，将这36500只蜜蜂的样本的飞行距离进行排序。我们认为95%的蜜蜂的活动范围为该种群的绝对范围，于是 将第95*365只蜜蜂的飞行距离为该绝对范围的绝对半径。于是就得到了绝对范围，用81000平方米除以该绝对范围即可得到所需的蜜蜂的种群数量。

具体代码如下：

#include 
#include 
#include 
#include 
#include 
#include 
using namespace std;

struct month_wearher
{
	int low = 0;
	int high = 0;
	int max = 0;
	int min = 0;
};



int main()
{
	srand((unsigned int)time(NULL));
	month_wearher wea[13];
	wea[1].low = 12, wea[1].high = 20, wea[1].max = 25, wea[1].min = 3;
	wea[2].low = 13, wea[2].high = 20, wea[2].max = 25, wea[2].min = 1;
	wea[3].low = 16, wea[3].high = 21, wea[3].max = 27, wea[3].min = 6;
	wea[4].low = 22, wea[4].high = 22, wea[4].max = 32, wea[4].min = 9;
	wea[5].low = 24, wea[5].high = 28, wea[5].max = 37, wea[5].min = 16;
	wea[6].low = 28, wea[6].high = 29, wea[6].max = 38, wea[6].min = 19;
	wea[7].low = 30, wea[7].high = 32, wea[7].max = 39, wea[7].min = 24;
	wea[8].low = 30, wea[8].high = 36, wea[8].max = 37, wea[8].min = 22;
	wea[9].low = 28, wea[9].high = 30, wea[9].max = 38, wea[9].min = 19;
	wea[10].low = 23, wea[10].high = 25, wea[10].max = 36, wea[10].min = 0;
	wea[11].low = 15, wea[11].high = 25, wea[11].max = 30, wea[11].min = 10;
	wea[12].low = 10, wea[12].high = 25, wea[12].max = 28, wea[12].min = 5;
	int mon_day[13] = { 0,31,28,31,30,31,30,31,31,30,31,30,31 };
	int huafen[13] = { 0,4,5,21,76,100,74,57,31,35,25,23,11 };
	int round[40] = { 0,0,0,0,0,0,0,0,0,0,0,0,0,1,2,3,4,6,9,14,21,31,46,68,100,74,57,45,36,28,23,18,15,12,10,8,7,6,5,4 };
	int tian = 0,dex = 0;
	double r[36500] = { 0 };
	for (int month = 1; month <= 12; month++)
	{
		for (int day = 1; day <= mon_day[month]; day++)
		{
			tian++;
			int t;
			if (rand() % 40 == 0)t = rand() % (wea[month].low - wea[month].min + 1) + wea[month].min;
			else if (rand() % 40 == 39)t = rand() % (wea[month].max - wea[month].high + 1) + wea[month].high;
			else t = rand() % (wea[month].high - wea[month].low + 1) + wea[month].low;
			double r0 = round[t]*0.05 + 1;
			double r_min = r0 * 0.85;
			double r_max = r0 * 1.15;
			for (int i = 0; i < 100; i++)
			{
				int t = rand() % 20;
				if (t != 19)
				{
					double x = r_min + (rand() % 101) * (r_max - r_min) / 100;
					r[dex] = x;
					dex++;
				}
				else
				{
					double x = r_max + (rand() % 101) * (20 - r_max) / 100;
					r[dex] = x;
					dex++;
				}
			}
		}
	}
	sort(r,r+36500);
	double m = r[365 * 95];
	cout << "一个蜂巢所需的空间半径为：" << m << "KM" << endl;
	cout << "20英亩所需要的蜂群数为:"<<(int)(81000 / (3.14 * m * m))<

        经过多次模拟，我们得到的一共蜂巢所需的空间半径约为6.5KM，20英亩所需的蜂巢数在500-600之间。

第四问：

        撰写专属blog。

        这就是第四问的答案咯，这也是我第一次写blog，希望大家多多支撑！

        也希望我的这篇blog能够给大家提供一些思路，还有许多不足的地方希望大家指正！

        写到最后也希望一些C++大佬能够改进我的代码，大家一起共同进步！

        祝看到这篇blog的各位，学习进步，工作顺利，天天开心！