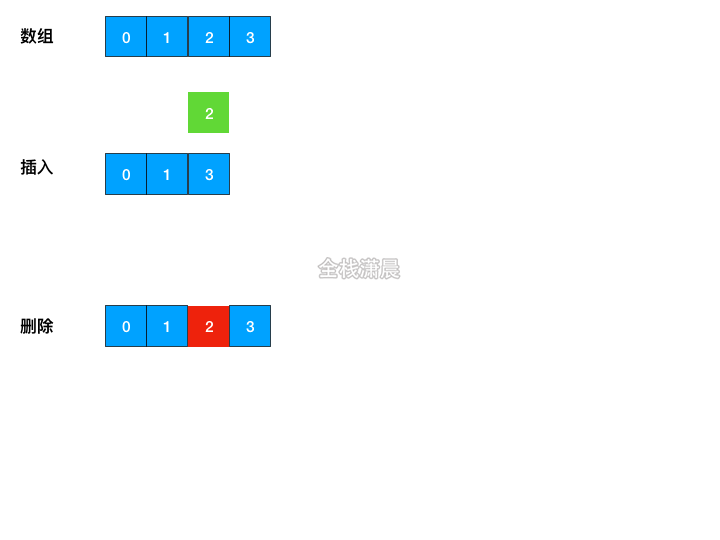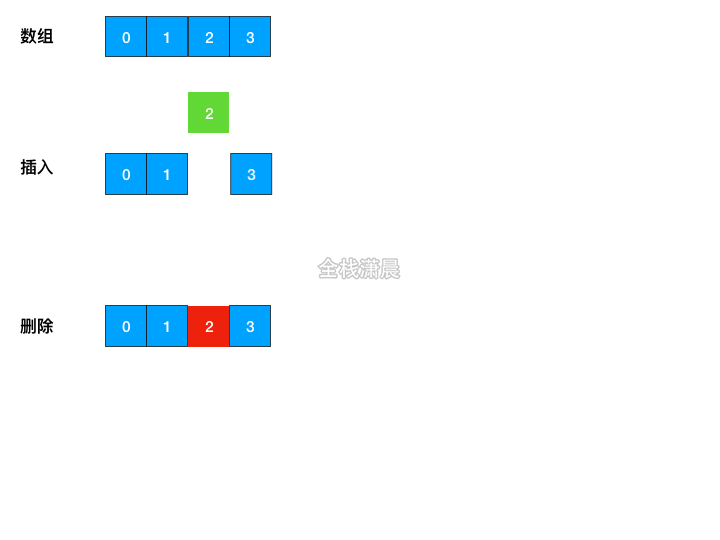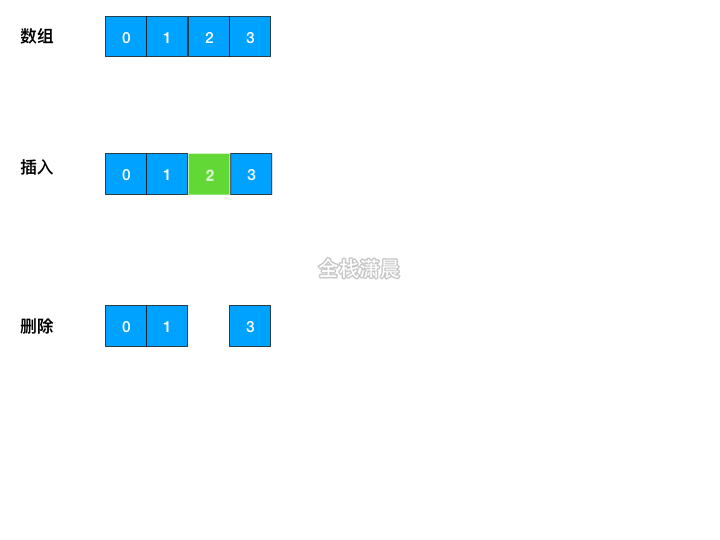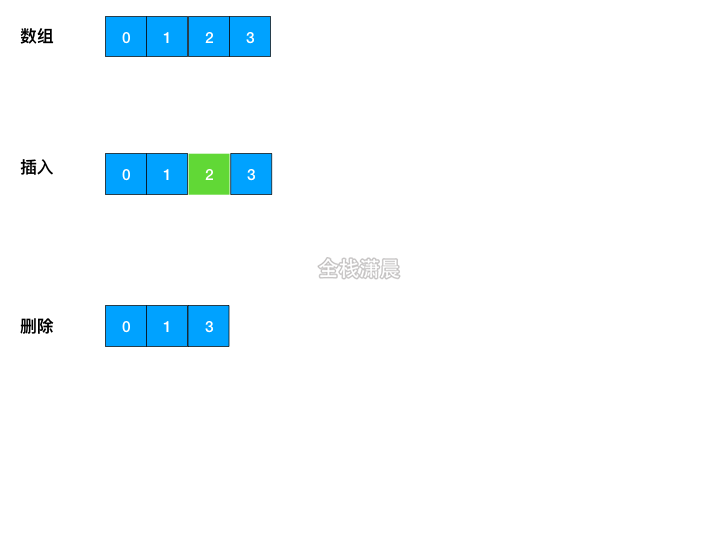
数组操作的时间复杂度
- Access:
O(1) - Search:
O(n) - Insert: 平均
O(n),最好的情况下O(1),也就是在数组尾部插入O(1),最坏的情况下O(n) - Delete;平均
O(n),最好的情况下O(1),也就是在数组尾部删除O(1),最坏的情况下O(n)
167. 两数之和 II - 输入有序数组 (easy)
给你一个下标从 1 开始的整数数组 numbers ,该数组已按 非递减顺序排列 ,请你从数组中找出满足相加之和等于目标数 target 的两个数。如果设这两个数分别是 numbers[index1] 和 numbers[index2] ,则 1 <= index1 < index2 <= numbers.length 。
以长度为 2 的整数数组 [index1, index2] 的形式返回这两个整数的下标 index1 和 index2。
你可以假设每个输入 只对应唯一的答案 ,而且你 不可以 重复使用相同的元素。
你所设计的解决方案必须只使用常量级的额外空间。
示例 1:
输入:numbers = [2,7,11,15], target = 9
输出:[1,2]
解释:2 与 7 之和等于目标数 9 。因此 index1 = 1, index2 = 2 。返回 [1, 2] 。
示例 2:输入:numbers = [2,3,4], target = 6
输出:[1,3]
解释:2 与 4 之和等于目标数 6 。因此 index1 = 1, index2 = 3 。返回 [1, 3] 。
示例 3:输入:numbers = [-1,0], target = -1
输出:[1,2]
解释:-1 与 0 之和等于目标数 -1 。因此 index1 = 1, index2 = 2 。返回 [1, 2] 。提示:
2 <= numbers.length <= 3 * 104
-1000 <= numbers[i] <= 1000
numbers 按 非递减顺序 排列
-1000 <= target <= 1000
仅存在一个有效答案
方法1:二分法
- 思路:循环数组,从当前元素右边的元素二分查找另一个元素,使他们的和是
target - 复杂度:时间复杂度
O(nlogn),遍历数组,每次遍历都进行了二分。空间复杂度O(1)
js:
var twoSum = function (numbers, target) {
let len = numbers.length,
left = 0,
right = len - 1,
mid = 0
for (let i = 0; i < len; ++i) {//循环数组,从右边的元素二分查找另一个元素
left = i + 1
while (left <= right) {
mid = parseInt((right - left) / 2) + left
if (numbers[mid] == target - numbers[i]) {
return [i + 1, mid + 1]
} else if (numbers[mid] > target - numbers[i]) {
right = mid - 1
} else {
left = mid + 1
}
}
}
return [-1, -1]
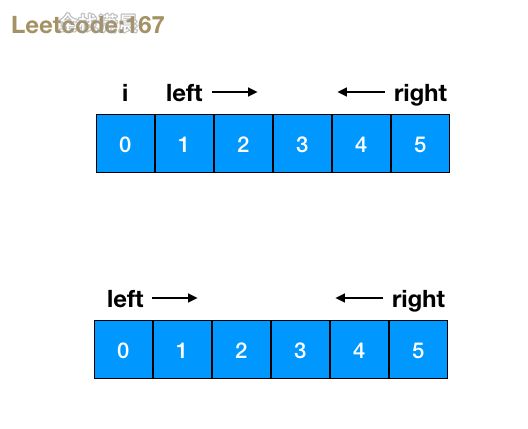
}方法2:双指针
- 思路:应以left和right指针,初始分别在数组的两端,然后不断判断两个指针指向的数字之和 和target的大小,和大了 ,right左移一位,和小了,left右移一位
- 复杂度:时间复杂度
O(n),数组总共遍历一次。空间复杂度O(1)
js:
var twoSum = function (numbers, target) {
let [left, right] = [0, numbers.length - 1];//左右指针
while (left < right) {//
if (numbers[left] + numbers[right] > target) {//和大了 right左移一位
right--;
} else if (numbers[left] + numbers[right] < target) {//和小了left右移一位
left++;
} else {
return [left + 1, right + 1];
}
}
};349. 两个数组的交集 (easy)
给定两个数组 nums1 和 nums2 ,返回 它们的交集 。输出结果中的每个元素一定是 唯一 的。我们可以 不考虑输出结果的顺序 。
示例 1:
输入:nums1 = [1,2,2,1], nums2 = [2,2]
输出:[2]
示例 2:输入:nums1 = [4,9,5], nums2 = [9,4,9,8,4]
输出:[9,4]
解释:[4,9] 也是可通过的提示:
1 <= nums1.length, nums2.length <= 1000
0 <= nums1[i], nums2[i] <= 1000
方法1:集合
- 思路:先将数组转成set,然后遍历长度小的set,判断set1中的元素是否存在于set2中,存在的话就是其中一个交集。
- 复杂度:时间复杂度
O(m+n),m,n是两数组的长度,数组转成集合的时间复杂度就是数组的长度,遍历寻找交集的复杂度是O(min(m,n))。空间复杂度O(m+n),就是两个set的空间
js:
var intersection = function (nums1, nums2) {
let set1 = new Set(nums1);
let set2 = new Set(nums2);//数组转成set
if (set1.size > set2.size) {//用size小的数组遍历
[set1, set2] = [set2, set1]
}
const intersection = new Set();
for (const num of set1) {//遍历set1
if (set2.has(num)) {//元素如果不存在于set2中就加入intersection
intersection.add(num);
}
}
return [...intersection];//转成数组
};方法2:排序+双指针
- 思路:数组排序,然后用两个指针分别遍历数组,如果两个指针指向的元素相等 就是其中一个交集,否则比较两个指针指向的元素的大小,较小的向前移动
- 复杂度:时间复杂度
O(mlogm+nlogn),两数组快排时间复杂度分别是O(mlogm)、O(nlogn),双指针遍历需要O(m+n),复杂度取决于较大的O(mlogm+nlogn)。空间复杂度O(logm+logn)排序使用的额外空间
js:
// nums1 = [4,5,9]
// nums2 = [4,4,8,9,9]
// intersection = [4,9]
var intersection = function (nums1, nums2) {
nums1.sort((x, y) => x - y);//排序
nums2.sort((x, y) => x - y);
const length1 = nums1.length,
length2 = nums2.length;
let index1 = 0,//双指针
index2 = 0;
const intersection = [];
while (index1 < length1 && index2 < length2) {//双指针遍历数组
const num1 = nums1[index1],
num2 = nums2[index2];
if (num1 === num2) {//如果两个指针指向的元素相等 就时其中一个交集
//防止重复加入
if (num1 !== intersection[intersection.length - 1]) {
intersection.push(num1);
}
index1++;
index2++;
} else if (num1 < num2) {
index1++;//num1 < num2说明mums1需要向右移动
} else {
index2++;//num1 > num2说明mums1需要向左移动
}
}
return intersection;
};217. 存在重复元素 (easy)
给你一个整数数组 nums 。如果任一值在数组中出现 至少两次 ,返回 true ;如果数组中每个元素互不相同,返回 false 。
示例 1:
输入:nums = [1,2,3,1]
输出:true
示例 2:输入:nums = [1,2,3,4]
输出:false
示例 3:输入:nums = [1,1,1,3,3,4,3,2,4,2]
输出:true提示:
1 <= nums.length <= 105
-109 <= nums[i] <= 109
方法1.排序
- 思路:先排序,然后循环数组,判断相邻元素是否相同
- 复杂度:时间复杂度
O(nlogn),空间复杂度O(logn),排序需要的栈空间
js:
var containsDuplicate = function(nums) {
nums.sort((a, b) => a - b);//排序
const n = nums.length;
for (let i = 0; i < n - 1; i++) {
if (nums[i] === nums[i + 1]) {//判断相邻元素是否相同
return true;
}
}
return false;
};方法2.哈希表
- 思路:循环数组,将元素存入set,判断每个元素是否存在于set中
- 复杂度:时间复杂度
O(n),空间复杂度O(n)
js:
var containsDuplicate = function(nums) {
const set = new Set();
for (const x of nums) {
if (set.has(x)) {
return true;
}
set.add(x);
}
return false;
};905. 按奇偶排序数组 (easy)
给你一个整数数组 nums,将 nums 中的的所有偶数元素移动到数组的前面,后跟所有奇数元素。
返回满足此条件的 任一数组 作为答案。
示例 1:
输入:nums = [3,1,2,4]
输出:[2,4,3,1]
解释:[4,2,3,1]、[2,4,1,3] 和 [4,2,1,3] 也会被视作正确答案。
示例 2:输入:nums = [0]
输出:[0]提示:
1 <= nums.length <= 5000
0 <= nums[i] <= 5000
方法1.排序
- 思路:排序比较,偶数在前,奇数在后
- 复杂度:时间复杂度
O(nlogn),空间复杂度O(logn),排序额外的空间
js:
var sortArrayByParity = function(A) {
return A.sort((a, b) => (a & 1) - (b & 1))
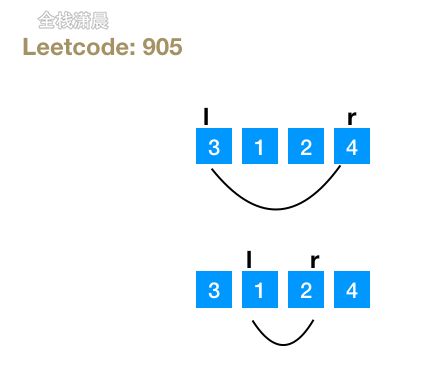
};方法2.双指针
- 思路:右指针从右往左,直到遇到第一个偶数,左指针从左往右,直到遇到第一个奇数,然后交换位置
- 复杂度:时间复杂度
O(n),空间复杂度O(1)
js:
var sortArrayByParity = function(A, l = 0, r = A.length - 1) {
while(l !== r) {
while (r > 0 && A[r] & 1) r--
while (l < r && (A[l] & 1) === 0) l++
[A[l], A[r]] = [A[r], A[l]]
}
return A
};75. 颜色分类 (medium)
给定一个包含红色、白色和蓝色、共 n 个元素的数组 nums ,原地对它们进行排序,使得相同颜色的元素相邻,并按照红色、白色、蓝色顺序排列。
我们使用整数 0、 1 和 2 分别表示红色、白色和蓝色。
必须在不使用库的sort函数的情况下解决这个问题。
示例 1:
输入:nums = [2,0,2,1,1,0]
输出:[0,0,1,1,2,2]
示例 2:输入:nums = [2,0,1]
输出:[0,1,2]提示:
n == nums.length
1 <= n <= 300
nums[i] 为 0、1 或 2进阶:
你可以不使用代码库中的排序函数来解决这道题吗?
你能想出一个仅使用常数空间的一趟扫描算法吗?
方法1.双指针
思路:准备p0,p1两个指针,p0指向0元素,p1指向1,初始化的时候,两个指针都指向数组的第一个位置。然后循环数组
- 遇见1就交换当前元素和p1,让p1加1,向前移动一位
- 遇见0就交换当前元素和p0,如果p1小于p0,则此时p0指向的元素是1,与i位置元素交换之后 这个交换过去的1位置就不对了,所以交换过去的1需要在和p1交换一下,这时p0和p1都指向了正确的元素,所以都需要向前移动一次。如果p0等于p1,则前面的元素都是0,所以p0和p1也要向前移动一次
- 复杂度:时间复杂度
O(n),n是数组的长度,空间复杂O(1)
js:
var sortColors = function (nums) {
let p0 = 0 //指向0
let p1 = 0 //指向0
for (let i = 0; i < nums.length; i++) {
if (nums[i] === 1) {//如果当前i指向的元素等于1,则交换当前元素和p1指向的元素
let temp = nums[p1]
nums[p1] = nums[i]
nums[i] = temp
p1++
} else if (nums[i] === 0) {//如果当前i指向的元素等于0,则交换当前元素和p0指向的元素
let temp = nums[p0]
nums[p0] = nums[i]
nums[i] = temp
//如果p0小于p1 则此时p0指向的元素是1,与i位置元素交换之后 这个交换过去的1位置就不对了 所以交换过去的1需要在和p1交换一下
if (p0 < p1) {
temp = nums[i];
nums[i] = nums[p1];
nums[p1] = temp;
}
//每次交换0之后都要移动p0和p1,如果p0===p1,则前面都是0,如果p0方法2.双指针
思路:准备两指针,p0指向元素0,它左边的都是0,p2指向2,它右边都是2,然后循环数组,当循环到了p2,说明p2右边的元素都是正确的数,所以
i<=p2- 如果此时i指向元素2 i小于p2 则不断交换p2和i指向的元素 因为交换过来的数可能还是2,那这个2就处于不正确的位置了
- 如果此时i指向元素0 则交换p0和i指向的元素
- 循环完成则0和2都拍好了,中间的1自然也是正确的位置
- 复杂度:时间复杂度
O(n),n是数组的长度,空间复杂O(1)
js:
var sortColors = function (nums) {
let p0 = 0;//指向0
let p2 = nums.length - 1;//指向2
for (let i = 0; i <= p2; i++) {//当循环到了p2 说明p2右边的元素都是正确的数,所以i<=p2
//如果此时i指向元素2 i小于p2 则不断交换p2和i指向的元素 因为交换过来的数可能还是2,那这个2就处于不正确的位置了
while (nums[i] === 2 && i < p2) {
let temp = nums[i];
nums[i] = nums[p2];
nums[p2] = temp;
p2--;
}
//如果此时i指向元素0 则交换p0和i指向的元素
if (nums[i] === 0) {
let temp = nums[i];
nums[i] = nums[p0];
nums[p0] = temp;
p0++;
}
}
};
//写法2
var sortColors = function (nums) {
const swap = (list, p1, p2) => [list[p1], list[p2]] = [list[p2], list[p1]]
let red = 0,
blue = nums.length - 1,
p = 0
while (p <= blue) {
switch (nums[p]) {
case 0:
swap(nums, red++, p)
p++
break;
case 1://遇见1 一直让p++ 这样即使交换过来的是2 也是处于正确的位置
p++
break;
case 2:
swap(nums, blue--, p)
break;
default:
break;
}
}
};283. 移动零 (easy)
给定一个数组 nums,编写一个函数将所有 0 移动到数组的末尾,同时保持非零元素的相对顺序。
请注意 ,必须在不复制数组的情况下原地对数组进行操作。
示例 1:
输入: nums = [0,1,0,3,12]
输出: [1,3,12,0,0]
示例 2:输入: nums = [0]
输出: [0]提示:
1 <= nums.length <= 104
-231 <= nums[i] <= 231 - 1进阶:你能尽量减少完成的操作次数吗?
方法1:两次遍历
- 思路:遍历数组,定义索引j为数组的第一个位置,遇上非0元素,让j位置上的元素等于这个非0元素,遍历完数组之后,j位置之后的元素全部置为0
- 复杂度:时间复杂度
O(n),空间复杂度O(1)
js:
var moveZeroes = function (nums) {
let j = 0;
for (let i = 0; i < nums.length; i++) {
if (nums[i] !== 0) {//遇到非0元素,让nums[j] = nums[i],然后j++
nums[j] = nums[i];
j++;
}
}
for (let i = j; i < nums.length; i++) {//剩下的元素全是0
nums[i] = 0;
}
return nums;
};方法2:双指针一次遍历
- 思路:定义left、right指针,right从左往右移动,遇上非0元素,交换left和right对应的元素,交换之后
left++ - 复杂度:时间复杂度
O(n),空间复杂度O(1)
js:
var moveZeroes = function(nums) {
let left=0,right=0
while(right350. 两个数组的交集 II (easy)
给你两个整数数组 nums1 和 nums2 ,请你以数组形式返回两数组的交集。返回结果中每个元素出现的次数,应与元素在两个数组中都出现的次数一致(如果出现次数不一致,则考虑取较小值)。可以不考虑输出结果的顺序。
示例 1:
输入:nums1 = [1,2,2,1], nums2 = [2,2]
输出:[2,2]
示例 2:输入:nums1 = [4,9,5], nums2 = [9,4,9,8,4]
输出:[4,9]提示:
1 <= nums1.length, nums2.length <= 1000
0 <= nums1[i], nums2[i] <= 1000进阶:
如果给定的数组已经排好序呢?你将如何优化你的算法?
如果 nums1 的大小比 nums2 小,哪种方法更优?
如果 nums2 的元素存储在磁盘上,内存是有限的,并且你不能一次加载所有的元素到内存中,你该怎么办?
方法1:哈希表
- 思路:统计nums1中各个元素的频次,循环nums2,看nums2中的元素是否在mums1频数哈希表中存在,存在的话加入结果,并且频数减1
- 复杂度:时间复杂度
O(m+n),遍历两个数组,哈希表操作复杂度是O(1)。空间复杂度O(min(m,n))对长度小的数组进行哈希。
js:
const intersect = (nums1, nums2) => {
const map = {};
const res = [];
if (nums1.length < nums2.length) {
[nums1, nums2] = [nums2, nums1]
}
for (const num1 of nums1) {//nums1中各个元素的频次
if (map[num1]) {
map[num1]++;
} else {
map[num1] = 1;
}
}
for (const num2 of nums2) { //遍历nums2
const val = map[num2];
if (val > 0) { //在nums1中
res.push(num2); //加入res数组
map[num2]--; //匹配掉一个,就减一个
}
}
return res;
};方法2:双指针
- 思路:p1,p2双指针指向两数组中的元素,在p1,p2都不越界的情况下开始循环,如果p1指向的元素大,移动p2,如果p2指向的元素大,移动p1,遇到相同则加入入res,移动两指针
- 复杂度:时间复杂度
O(mlogm+nlogn),m、n分别是数组的长度,排序时间复杂度是O(mlogm+nlogn),两数组遍历是O(m+n)。空间复杂度O(logm+logn)
js:
const intersect = (nums1, nums2) => {
nums1.sort((a, b) => a - b);
nums2.sort((a, b) => a - b); //排序两个数组
const res = [];
let p1 = 0;//指向nums1中的元素
let p2 = 0;//指向nums2中的元素
while (p1 < nums1.length && p2 < nums2.length) {//不越界条件
if (nums1[p1] > nums2[p2]) {//p1指向的元素大,移动p2
p2++;
} else if (nums1[p1] < nums2[p2]) {//p2指向的元素大,移动p1
p1++;
} else {
//遇到相同则加入入res,移动两指针
res.push(nums1[p1]);
p1++;
p2++;
}
}
return res;
};238. 除自身以外数组的乘积 (medium)
给你一个整数数组 nums,返回 数组 answer ,其中 answer[i] 等于 nums 中除 nums[i] 之外其余各元素的乘积 。
题目数据 保证 数组 nums之中任意元素的全部前缀元素和后缀的乘积都在 32 位 整数范围内。
请不要使用除法,且在 O(n) 时间复杂度内完成此题。
示例 1:
输入: nums = [1,2,3,4]
输出: [24,12,8,6]
示例 2:输入: nums = [-1,1,0,-3,3]
输出: [0,0,9,0,0]提示:
2 <= nums.length <= 105
-30 <= nums[i] <= 30
保证 数组 nums之中任意元素的全部前缀元素和后缀的乘积都在 32 位 整数范围内进阶:你可以在 O(1) 的额外空间复杂度内完成这个题目吗?( 出于对空间复杂度分析的目的,输出数组不被视为额外空间。)
- 思路:从左往右遍历,记录从左到当前位置前一位的乘积,然后从右往左遍历,从左到当前位置前一位的乘积乘上右边元素的积。
- 复杂度:时间复杂度
O(n),空间复杂度O(1)
js:
var productExceptSelf = function (nums) {
const res = [];
res[0] = 1;
//从左往右遍历
//记录从左到当前位置前一位的乘积
for (let i = 1; i < nums.length; i++) {
res[i] = res[i - 1] * nums[i - 1];
}
let right = 1;
//从右往左遍历
//从左到当前位置前一位的乘积 乘上 右边元素的积
for (let j = nums.length - 1; j >= 0; j--) {
res[j] *= right;
right *= nums[j];
}
return res;
};209. 长度最小的子数组 (medium)
给定一个含有 n 个正整数的数组和一个正整数 target 。
找出该数组中满足其和 ≥ target 的长度最小的 连续子数组 [numsl, numsl+1, ..., numsr-1, numsr] ,并返回其长度。如果不存在符合条件的子数组,返回 0 。
示例 1:
输入:target = 7, nums = [2,3,1,2,4,3]
输出:2
解释:子数组 [4,3] 是该条件下的长度最小的子数组。
示例 2:输入:target = 4, nums = [1,4,4]
输出:1
示例 3:输入:target = 11, nums = [1,1,1,1,1,1,1,1]
输出:0提示:
1 <= target <= 109
1 <= nums.length <= 105
1 <= nums[i] <= 105
方法1:滑动窗口
- 思路:左右指针是滑动窗口的两边,用滑动窗口循环数组,不断扩大窗口,如果窗口中元素的和大于target,就开始缩小窗口,然后更新最小滑动窗口
- 复杂度:时间复杂度
O(n),数组中的元素都遍历一次,空间复杂度O(1)
js:
var minSubArrayLen = function(target, nums) {
const len = nums.length;
let l = r = sum = 0,
res = len + 1; //最大的窗口不会超过自身长度
while(r < len) {
sum += nums[r++];//扩大窗口
while(sum >= target) {
res = res < r - l ? res : r - l;//更新最小值
sum-=nums[l++];//缩小窗口
}
}
return res > len ? 0 : res;
};922. 按奇偶排序数组 II (easy)
给定一个非负整数数组 nums, nums 中一半整数是 奇数 ,一半整数是 偶数 。
对数组进行排序,以便当 nums[i] 为奇数时,i 也是 奇数 ;当 nums[i] 为偶数时, i 也是 偶数 。
你可以返回 任何满足上述条件的数组作为答案 。
示例 1:
输入:nums = [4,2,5,7]
输出:[4,5,2,7]
解释:[4,7,2,5],[2,5,4,7],[2,7,4,5] 也会被接受。
示例 2:输入:nums = [2,3]
输出:[2,3]提示:
2 <= nums.length <= 2 * 104
nums.length 是偶数
nums 中一半是偶数
0 <= nums[i] <= 1000进阶:可以不使用额外空间解决问题吗?
方法1.双指针
- 思路:循环偶数位置 如果遇到了奇数,然后循环奇数位置 如果遇到了第一个偶数,就交位
- 复杂度:时间复杂度
O(n),空间复杂度O(1)
js:
const swap = (nums, i, j) => {
const temp = nums[i];
nums[i] = nums[j];
nums[j] = temp;
};
var sortArrayByParityII = function(nums) {
const n = nums.length;
let j = 1;
for (let i = 0; i < n; i += 2) {
if (nums[i] & 1) {//循环偶数位置 如果遇到了奇数
while (nums[j] & 1) {//循环奇数位置 如果遇到了第一个偶数
j += 2;
}
swap(nums, i, j);//交位置换
}
}
return nums;
};视频讲解:传送门