SVM -- R的演示及应用示例

对于SVM算法的介绍，如下几篇文章应该是讲得比较详细清楚的了：

• 基础：http://blog.csdn.net/zouxy09/article/details/17291543/

• 进阶：http://blog.csdn.net/zouxy09/article/details/17291805

• Python的实现:http://blog.csdn.net/zouxy09/article/details/17292011

所以这里我主要要说的便是SVM算法基于R的演示及应用实例。

函数介绍

kernlab包中的ksvm函数、e1071包中的svm函数、klaR包中的svmlight函数、svmpath包中的svmpath函数等都可以实现SVM算法。

svm函数
e1071包中的svm函数可以实现二分类和多分类的支持向量分类、支持向量回归以及异常点探测等，其基本语法如下：

svm(formula=R公式， data=数据集名称， scale=TRUE/FALSE， type=支持向量机类型， kernel=核函数名， gamma=g， degree=d， 
cost=C， epsilon=0.1， na.action=na.omit/na.fail)

参数说明如下：

formula：以R公式的形式指定输出变量和输入变量，其格式一般为：输出变量名~输入变量名。数据都存储在了指定的dataframe中

---

scale:取TRUE/FALSE,分别表示建模前是否对数据进行标准化处理，以消除变量数量级对距离计算的影响

---

type:指定支持向量机的类型，可能的取值有”C-classification”，”eps-re-gression”等，分别表示支持向量分类C-SVM和以 ϵ− 不敏感损失函数为基础的支持向量回归

---

kernel:用于指定多项式核函数名称，可能的取值有”linear”,”polynomial”,”radialbasis”等，分别表示线性核、多项式核和径向基核

---

gamma:用于指定多项式核以及径向基核中的参数 γ ，R默认gamma是线性核中的常数项，等于1/p(p为特征空间中的维度)

---

degree：用于指定多项式核中的阶数d

---

cost:用于指定损失惩罚函数参数C

---

epsilon：用于指定支持向量回归中的 ϵ− 带，default value为0.1

---

na.action：取na.omit表示忽略数据中带有缺失值的观测，去na.fail表示如果缺失观测将报错

---

svm函数的返回结果是包含多个成分的列表，主要成分如下：

SV：给出支持向量观测在所有变量上的取值

index:给出个支持向量的观测编号

decision.values：将个观测带入决策函数给出决策函数值。依据决策函数值的正负，预测观测所属类别

---

tune.svm函数
损失惩罚函数C以及核函数的参数都是支持向量机中的重要参数。可通过交叉验证的方式确定参数。tune.svm函数可自动实现10折交叉验证，并给出预测误差最小时的参数值。其基本语法如下：

tune.svm(formula=R公式， data=数据集名称， scale=TRUE/FALSE， type=支持向量机类型， kernel=核函数类型， gamma=参数向量， 
degree=参数向量， cost=参数向量， na.action=na.omit/na.fail)

tune.svm函数的参数与svm基本相同，不同的是此处的参数gamma、degree、cost应设置为一个包含所有可能参数值的向量。

tune.svm函数的返回是个列表对象，包括best.parameters, best.performance, best.model成分，存储预测误差最小时的参数、预测误差以及相应参数下的模型的基本信息等。

模拟线性可分下的支持向量分类

主要模拟步骤如下：

• 第一，在线性可分的原则下，随机生成训练样本集合测试样本集。其中的输入变量有2个，输出变量类别为-1和+1

#############模拟线性可分下的SVM####################
set.seed(12345)

## 生成40个观测
x<-matrix(rnorm(n=40*2,mean=0,sd=1),ncol=2,byrow=TRUE)
y<-c(rep(-1,20),rep(1,20))

## 对后二十个观测值加上1.5
x[y==1,]<-x[y==1,]+1.5

#生成训练样本集,前二十个观测标签为-1，后二十个位+1
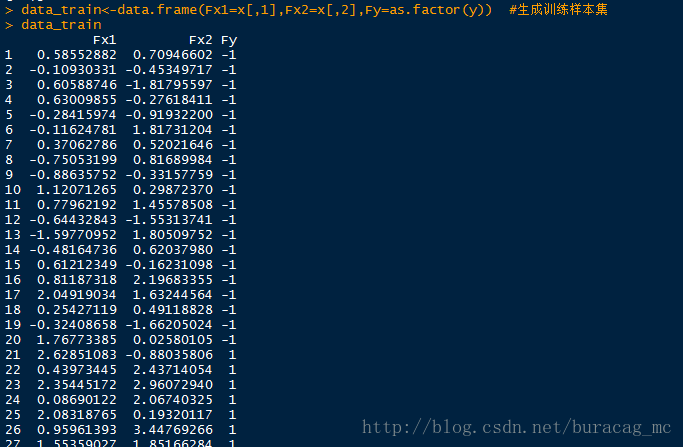
data_train<-data.frame(Fx1=x[,1],Fx2=x[,2],Fy=as.factor(y)) 

#生成测试样本集
x<-matrix(rnorm(n=20,mean=0,sd=1),ncol=2,byrow=TRUE)
y<-sample(x=c(-1,1),size=10,replace=TRUE)
x[y==1,]<-x[y==1,]+1.5
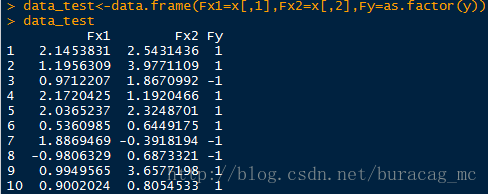
data_test<-data.frame(Fx1=x[,1],Fx2=x[,2],Fy=as.factor(y)) 

画个散点图看看：

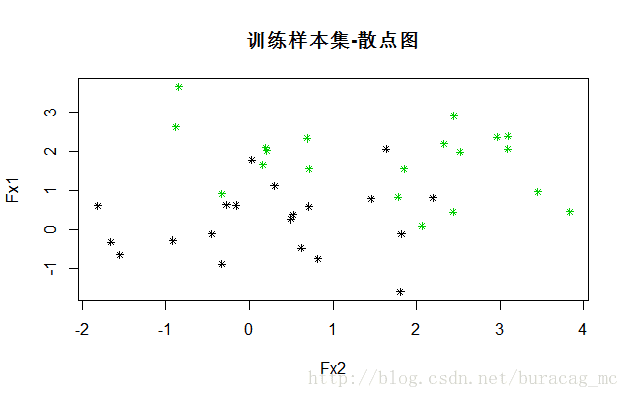
plot(data_train[,2:1],col=as.integer(as.vector(data_train[,3]))+2,pch=8,cex=0.7,main="训练样本集-散点图")

---

• 第二，采用线性核函数，比较当损失惩罚参数较大和较小时的支持向量个数和最大边界超平面

library("e1071")

## 线性SVM
SvmFit<-svm(Fy~.,data=data_train,type="Cclassification",kernel="linear",
cost=10,scale=FALSE)
summary(SvmFit)

可以看到，当损失函数参数C=10时，有16个支持向量(两类各有8个)

plot(x=SvmFit,data=data_train,formula=Fx1~Fx2,svSymbol="#",dataSymbol="*",grid=100)

SvmFit<-svm(Fy~.,data=data_train,type="C-classification",kernel="linear",cost=0.1,scale=FALSE)
summary(SvmFit)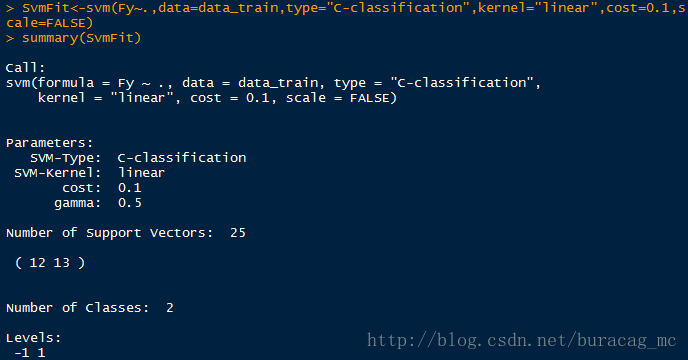

可以看到，当损失惩罚参数C=0.1时，由于惩罚程度降低，所有包含的支持向量增加到了25个。

---

• 第三，利用10折交叉验证找到预测误差最小时的损失惩罚参数

set.seed(12345)
tObj<-tune.svm(Fy~.,data=data_train,type="C-classification",kernel="linear", cost=c(0.001,0.01,0.1,1,5,10,100,1000),scale=FALSE)
summary(tObj)

## BEST model
BestSvm<-tObj$best.model
summary(BestSvm)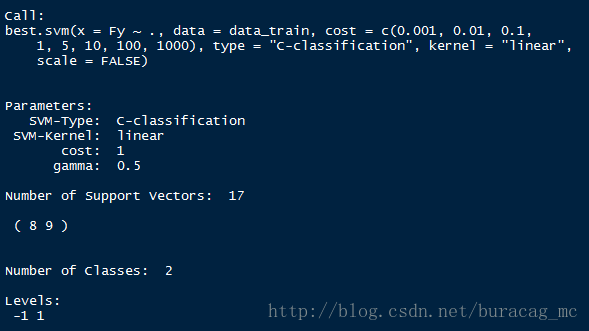

可以看到，采用10折交叉验证的预测误差最低时的C等于1，平均误判率为0.15。该参数下的模型为最优模型，找到了17个支持向量。

---

• 第四，利用最优模型对测试样本集

## 用10折交叉验证得到的best model测试
yPred<-predict(BestSvm,data_test)
(ConfM<-table(yPred,data_test$Fy))
(Err<-(sum(ConfM)-sum(diag(ConfM)))/sum(ConfM))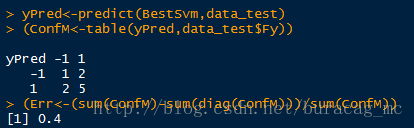

可以看到，将-1预测为+1的数量为2，将+1预测到-1的数量为2，故误判率为0.4。

模拟线性不可分下的支持向量分类

主要模拟步骤如下：

• 第一，在线性不可分的原则下，随机生成训练样本集合测试样本集。其中的输入变量有2个，输出变量类别为1和2。

set.seed(12345)
x<-matrix(rnorm(n=400,mean=0,sd=1),ncol=2,byrow=TRUE)
x[1:100,]<-x[1:100,]+2
x[101:150,]<-x[101:150,]-2
y<-c(rep(1,150),rep(2,50))
data<-data.frame(Fx1=x[,1],Fx2=x[,2],Fy=as.factor(y))

## 从1-200中随机抽选100个
flag<-sample(1:200,size=100)

## 100个为训练集
data_train<-data[flag,]

## 100个为测试集
data_test<-data[-flag,]

## 输出一下散点图
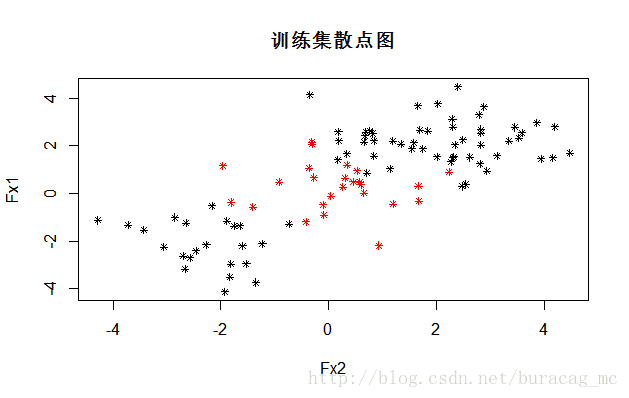
plot(data_train[,2:1],col=as.integer(as.vector(data_train[,3])),pch=8,cex=0.7,main="训练集散点图")

可见，样本集是一个线性不可分的，下面我们采用径向基核函数。

---

• 采用径向基核函数，利用10折交叉验证找到预测误差最小下的最优参数和最优模型

library("e1071")
set.seed(12345)

tObj<-tune.svm(Fy~.,data=data_train,type="C-classification",kernel="radial",    cost=c(0.001,0.01,0.1,1,5,10,100,1000),gamma=c(0.5,1,2,3,4),scale=FALSE)

## 可视化10折交叉验证后的不同参数组合下的结果
plot(tObj,xlab=expression(gamma),ylab="损失惩罚参数C",main="不同参数组合下的预测错误率",nlevels=10,color.palette=terrain.colors)

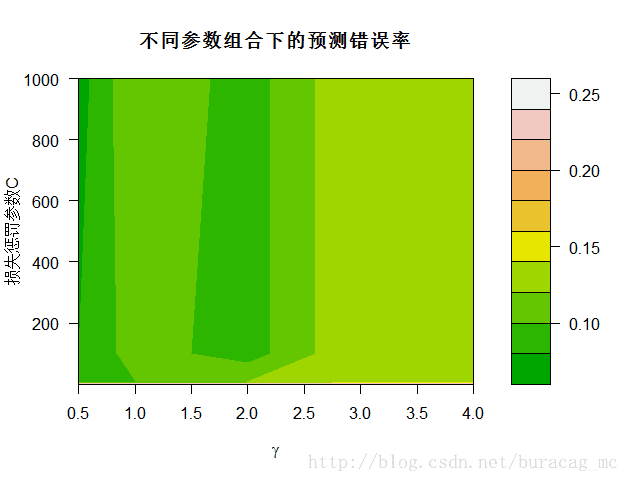
可以看到，颜色越深预测误差越小；即当gamma值等于0.5，C等于1000时，模型取最优，从summary结果也可以看出：

• 可视化超平面

plot(x=BestSvm,data=data_train,formula=Fx1~Fx2,svSymbol="#",dataSymbol="*",grid=100)

可以看到，支持向量(‘#’)位于两类的交汇处。

• 利用10折交叉验证训练的最优模型对测试集做预测

yPred<-predict(BestSvm,data_test)
(ConfM<-table(yPred,data_test$Fy))
(Err<-(sum(ConfM)-sum(diag(ConfM)))/sum(ConfM))

可以看到，预测误差率仅为0.08，说明训练所得模型效果的表现不错。

模拟多分类的支持向量分类

主要模拟步骤如下：

• 第一，在线性不可分的原则下，随机生成训练样本集；其中，输入变量有2个，输出变量有0,1和2三类。

set.seed(12345)
x<-matrix(rnorm(n=400,mean=0,sd=1),ncol=2,byrow=TRUE)
x[1:100,]<-x[1:100,]+2
x[101:150,]<-x[101:150,]-2
x<-rbind(x,matrix(rnorm(n=100,mean=0,sd=1),ncol=2,byrow=TRUE))
y<-c(rep(1,150),rep(2,50))
y<-c(y,rep(0,50))
x[y==0,2]<-x[y==0,2]+3
data<-data.frame(Fx1=x[,1],Fx2=x[,2],Fy=as.factor(y))

## 输出一下散点图
plot(data[,2:1],col=as.integer(as.vector(data[,3]))+1,pch=8,cex=0.7,main="训练集散点图")

可以看到，训练集总共包含250个观测，总共有3个类，说明该模拟时一个线性不可分下的多分类支持向量分类问题，我们采用径向基核函数。

• 采用径向基核函数，利用10折交叉验证找到预测误差最小下的最优参数和最优模型

library("e1071")
set.seed(12345)
tObj<-tune.svm(Fy~.,data=data,type="C-classification",kernel="radial",
               cost=c(0.001,0.01,0.1,1,5,10,100,1000),gamma=c(0.5,1,2,3,4),scale=FALSE)
BestSvm<-tObj$best.model
summary(BestSvm)

## 划分结果可视化下
plot(x=BestSvm,data=data,formula=Fx1~Fx2,svSymbol="#",dataSymbol="*",grid=100)

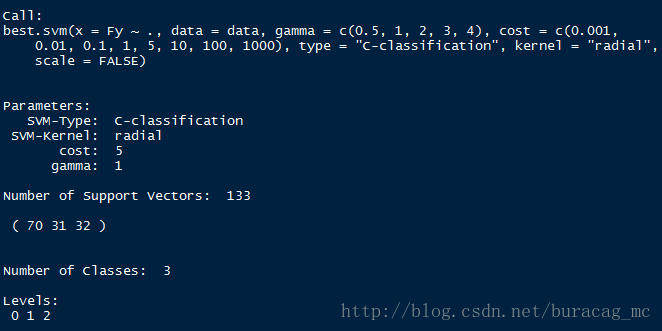
可以看到，最优模型时当C=5，gamma=1时的模型，模型将训练集划分结果如下：

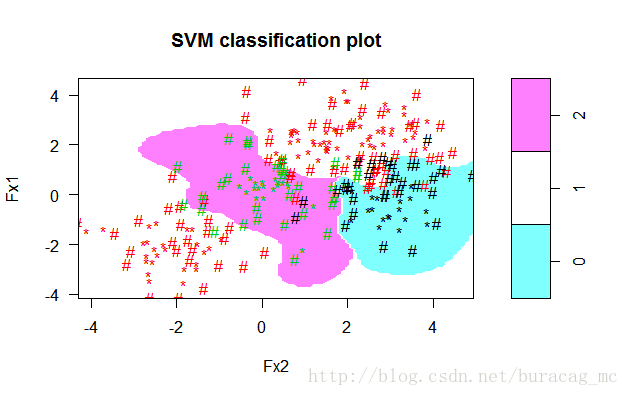
• 利用最优模型对训练样本做预测，观测多类别预测的依据。

SvmFit<-svm(Fy~.,data=data,type="C-classification",kernel="radial",cost=5,gamma=1,scale=FALSE)

head(SvmFit$decision.values)

## 预测
yPred<-predict(SvmFit,data)
(ConfM<-table(yPred,data$Fy))
(Err<-(sum(ConfM)-sum(diag(ConfM)))/sum(ConfM))

这里需要解读一下的是，head(SvmFit decision.values)命令：SvmFit decision.values查看个观测的决策函数值，head只是输出了头部的6个，以第一个观测为例，解释一下：

 对3个类别的分类问题建立了3个支持向量分类。在1对2(即1/2)类的分类中,决策函数值大于0，故预测为1类；

 在1对0(即1/0)类的分类中,决策函数值大于0，故预测为1类；

 在2对0(即2/0)类的分类中,决策函数值小于0，故预测为0类；

 预测为1类的次数最多，故最终观测1预测为1类。

可以看到，0类误判为1类和2类的数量分别为3和0；1类误判为0类和2类的数量分别为6和6；2类误判为0类和1类的数量分别为2和4。

总体预测误差为0.084，说明模型训练效果表现良好。