HOG算法复现

本博客纯粹用于记录学习过程中的error，若有好的想法或者对于程序某处有错误的，欢迎指点！谢谢

本文主要是了解一下HOG算法的执行机理，代码不一定正确，但是编译通过了，没有联合SVM进行测试，主要是还不会，若有后续，会测试一下。

我写了个图像的基本的一些处理的库，本程序中有些代码可能没给出来，基本都在那个库里，或许是挺简单的或者是之前的博客有，如果没有，就自己写吧，哈哈哈

1、HOG特征：

方向梯度直方图（Histogram of Oriented Gradient, HOG）特征是一种在计算机视觉和图像处理中用来进行物体检测的特征描述子。它通过计算和统计图像局部区域的梯度方向直方图来构成特征。Hog特征结合SVM分类器已经被广泛应用于图像识别中，尤其在行人检测中获得了极大的成功。需要提醒的是，HOG+SVM进行行人检测的方法是法国研究人员Dalal在2005的CVPR上提出的，而如今虽然有很多行人检测算法不断提出，但基本都是以HOG+SVM的思路为主。

（1）主要思想：

在一副图像中，局部目标的表象和形状（appearance and shape）能够被梯度或边缘的方向密度分布很好地描述。（本质：梯度的统计信息，而梯度主要存在于边缘的地方）。

（2）具体的实现方法是：

首先将图像分成小的连通区域，我们把它叫细胞单元。然后采集细胞单元中各像素点的梯度的或边缘的方向直方图。最后把这些直方图组合起来就可以构成特征描述器。

（3）提高性能：

把这些局部直方图在图像的更大的范围内（我们把它叫区间或block）进行对比度归一化（contrast-normalized），所采用的方法是：先计算各直方图在这个区间（block）中的密度，然后根据这个密度对区间中的各个细胞单元做归一化。通过这个归一化后，能对光照变化和阴影获得更好的效果。

（4）优点

与其他的特征描述方法相比，HOG有很多优点。首先，由于HOG是在图像的局部方格单元上操作，所以它对图像几何的和光学的形变都能保持很好的不变性，这两种形变只会出现在更大的空间领域上。其次，在粗的空域抽样、精细的方向抽样以及较强的局部光学归一化等条件下，只要行人大体上能够保持直立的姿势，可以容许行人有一些细微的肢体动作，这些细微的动作可以被忽略而不影响检测效果。因此HOG特征是特别适合于做图像中的人体检测的。

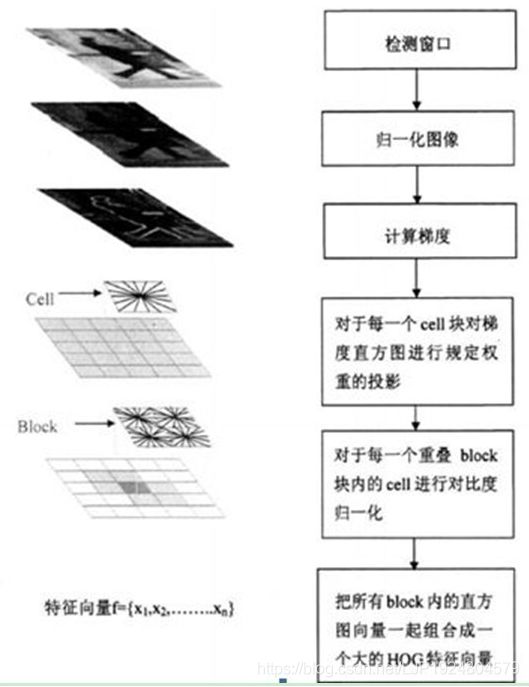
2、HOG特征提取算法的实现过程：

大概过程：

HOG特征提取方法就是将一个image（你要检测的目标或者扫描窗口）：

1）灰度化（将图像看做一个x,y,z（灰度）的三维图像）；

2）采用Gamma校正法对输入图像进行颜色空间的标准化（归一化）；目的是调节图像的对比度，降低图像局部的阴影和光照变化所造成的影响，同时可以抑制噪音的干扰；

3）计算图像每个像素的梯度（包括大小和方向）；主要是为了捕获轮廓信息，同时进一步弱化光照的干扰。

4）将图像划分成小cells（例如6*6像素/cell）；

5）统计每个cell的梯度直方图（不同梯度的个数），即可形成每个cell的descriptor；

6）将每几个cell组成一个block（例如3*3个cell/block），一个block内所有cell的特征descriptor串联起来便得到该block的HOG特征descriptor。

7）将图像image内的所有block的HOG特征descriptor串联起来就可以得到该image（你要检测的目标）的HOG特征descriptor了。这个就是最终的可供分类使用的特征向量了。

/*
HOG算法，
输入：图像，需要将360°分成多少格，块的尺寸
输出：一个二维的描述子
---2020/12/3
*/
#pragma once
#ifndef __HOGPROCESSIMAGE__
#define __HOGPROCESSIMAGE__

#include
#include"image_process.h"
#include"math.h"
#include"opencv.hpp"
using namespace std;
using namespace cv;
#define x 'x'
#define y 'y'
#define PI 3.14159265
/*创建二维数组*/
template<typename T>
T** CreatArray(int row, int col)
{
	int i;
	T** array = new T *[row]();
	for (i = 0; i < row; ++i)
		array[i] = new T[col]();
	return array;
}
/*将数组绝对值化*/
int** AbsoluteArray(int** array，int row,int col)
{
	int i, j;
	for (i = 0; i < row; ++i)
		for (j = 0; j < col; ++j)
			array[i][j] = abs(array[i][j]);
	return array;
}
/*求梯度x、y方向上的微分二维数组*/
int**ComputeGradient(Mat img,char direction)
{
	int row = img.rows;
	int col = img.cols;
	int i, j;
	int value;
	uchar* data_img;
	uchar* data1, * data2;
	//创建二维数组
	int** image = new int *[row]();
	for (i = 0; i < row; ++i)
		image[i] = new int[col]();
	if (direction == 'x')
	{
		for (i = 0; i < row; ++i)
		{
			data_img = img.ptr<uchar>(i);
			for(j = 1;j < col-1;++j)
			{ 
				value = (int)(data_img[j + 1] - data_img[j - 1]);
				image[i][j] = value;
			}
		}
	}
	else if (direction == 'y')
	{
		for (i = 1; i < row - 1; ++i)
		{
			data1 = img.ptr<uchar>(i - 1);
			data2 = img.ptr<uchar>(i + 1);
			for(j = 0;j < col; ++j)
			{
				value = (int)(data2[j] - data1[j]);
				image[i][j] = value;
			}
		}
	}
	else
	{
		cout << "输入计算梯度方向失败！" << endl;
		return 0;
	}
	return image;
}
/*求梯度方向*/
int**ComputeGradientAngle(int** ImageX, int**ImageY,int row, int col)
{
	int i, j;
	int** img = new int * [row]();
	for (i = 0; i < row; ++i)
		img[i] = new int[col]();
	for (i = 0; i < row; ++i)
	{
		for(j = 0;j < col; ++j)
		{
			img[i][j] = (int)(atan((float)ImageY[i][j]/(float)ImageX[i][j]) * 180 / PI);
		}
	}
	return img;
}
/*求梯度值*/
int** ComputeGradientValue(int** ImageX, int** ImageY,int row,int col)
{
	int i, j;
	int** img = new int * [row]();
	for (i = 0; i < row; ++i)
		img[i] = new int[col]();
	for (i = 0; i < row; ++i)
	{
		for (j = 0; j < col; ++j)
		{
			img[i][j] = (int)(sqrt(pow(ImageX[i][j],2)+pow(ImageY[i][j],2)));
		}
	}
	return img;
}
/*二维数组画图*/
Mat CreatImage(int** array, int row, int col)
{
	int i, j;
	uchar* data;
	Mat img(row, col, CV_8UC1);
	for (i = 0; i < row; ++i)
	{
		data = img.ptr<uchar>(i);
		for(j = 0;j < col; ++j)
		{
			data[j] = array[i][j];
		}
	}
	return img;
}
/*单元方向直方图*/
float** ComputeCellHistogram(int** ImageAngle, int** ImageValue,int AngleIntervalNumber,int CellSize,int row,int col)
{
	int i, j, k;
	int m, n;
	int new_i = 0, new_j = 0;
	int new_row = row / CellSize;//块数
	int new_col = col / CellSize;
	int t = 0;
	int location = 0;
	int value = 0;
	float PerAngleRange = (float)360 / AngleIntervalNumber;
	//创建保存直方图权值及方向的三维数组
	int*** img = new int**[new_row]();
	for (i = 0; i < new_row; ++i)
	{
		img[i] = new int* [new_col]();
		for (j = 0; j < new_col; ++j)
			img[i][j] = new int[AngleIntervalNumber]();
	}
	t = (new_row - 1) * (new_col - 1)*4;
	float** arr = CreatArray<float>(t, AngleIntervalNumber);//返回的hog描述符数组
	for(i = 0;i < row; i = i + CellSize)
	{
		for(j = 0;j < col; j = j + CellSize)
		{ 
			//得到每一个cell的梯度方向直方数组
			for (m = i; m < i + CellSize; ++m)
			{
				for (n = j ; n < j + CellSize; ++n)
				{
					location = ImageAngle[m][n]/ PerAngleRange;//
					if ((location < 0) || (location >= AngleIntervalNumber))
						break;
					img[new_i][new_j][location] = img[new_i][new_j][location] + ImageValue[m][n];
				}
			}
			new_j++;
		}
		new_i++;
		new_j = 0;
	}
	//采用2*2cells做特征提取
	new_i = 0;
	new_j = 0;
	for (i = 0; i < new_row-1; ++i)
	{
		for (j = 0; j < new_col-1; ++j)
		{
			//每2个cells取总值
			value = 0;
			for (m = i; m < i + 2; ++m)
			{
				for (n = j; n < j + 2; ++n)
				{
					for (k = 0; k < AngleIntervalNumber; ++k)
					{
						value = value + img[m][n][k] * img[m][n][k];
					}
				}
			}
			value = sqrt(value);
			//量化
			for (m = i; m < i + 2; ++m)
			{
				for (n = j; n < j + 2; ++n)
				{
					for (k = 0; k < AngleIntervalNumber; ++k)
					{
						arr[new_i][new_j] = (float)img[m][n][k]/value;//
						new_j++;
					}
					new_i++;
					new_j = 0;
				}
			}
		}
	}
	return arr;
}
/*主函数*/
float** HogProcessImage(Mat img, int AngleIntervalNumber = 9, int CellSize = 8)
{
	int row = img.rows;
	int col = img.cols;
	int row_rate, col_rate;
	Mat GrayImage, GammaImage, AngleImage, ValueImage;
	Mat image,gray;
	int** ImageX, ** ImageY, ** ImageAngle, ** ImageValue;
	float** HogArray;
	//改变图像尺寸，方便后面的块成形
	if ((row % CellSize != 0) || (col % CellSize != 0))
	{
		row_rate = row / CellSize;
		col_rate = col / CellSize;
		row = row_rate * CellSize;
		col = col_rate * CellSize;
		img = Change_Size(img,row,col);
	}
	gray = gray_image(img);
	GrayImage = gray_image(img);
	//伽马校验
	GammaImage = Gamma(GrayImage,1,1);
	//X,Y方向的微分二维数组
	ImageX = CreatArray<int>(row, col);
	ImageY = CreatArray<int>(row, col);
	ImageX = ComputeGradient(GammaImage, x);
	ImageY = ComputeGradient(GammaImage, y);
	ImageAngle = CreatArray<int>(row, col);
	ImageValue = CreatArray<int>(row, col);
	//计算权值以及角度
	ImageAngle = ComputeGradientAngle(ImageX, ImageY,row,col);
	ImageValue = ComputeGradientValue(ImageX, ImageY, row, col);
	ImageValue = AbsoluteArray(ImageValue,row,col);
	AngleImage = CreatImage(ImageAngle, row, col);
	ValueImage = CreatImage(ImageValue, row, col);
	//直方图
	HogArray = ComputeCellHistogram(ImageAngle, ImageValue, AngleIntervalNumber, CellSize, row, col);
	image = Merge_image(gray, GammaImage, AngleImage, ValueImage);
	return HogArray;
}
#endif

比较好的参考博客：
https://blog.csdn.net/hujingshuang/article/details/47337707
https://blog.csdn.net/zouxy09/article/details/7929348
https://blog.csdn.net/coming_is_winter/article/details/72850511
https://www.cnblogs.com/zyly/p/9651261.html