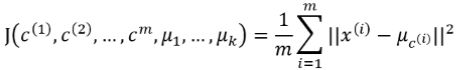K-means算法
一、k-means算法流程:
K-means是一种重要的无监督学习的算方法,也是聚类算法中的最常用的一种,算法的详细步骤如下:
1、在分类前选定K的值,即我们希望将数据集经过聚类得到K个类别;
2、从数据集中随机选择K个数据点作为质心(Centroid);
3、对数据集中的每个数据点中计算与这K个质心距离(一般选取欧式距离),数据集中每个样本点距离这K个质心中某个质心的距离最近,则这个数据样本被认为属于这个质心的类别;
4、在分好的K个类别中,计算每个类别所属的数据点的中心点作为新的K个质心;
5、如果新的质心和旧的质心的距离小于某一个设置的阈值(表示重新计算的质心的位置变化不大,趋于稳定,或者说收敛),可以认为我们进行的聚类已经达到期望的结果,算法终止;
6、如果新的质心和旧的质心的距离变化很大,需要迭代3~5步骤。
这样文字的叙述很难直观的理解K-means的算法过程,读者可以访问这个网站,该网址上可以通过简单的动图展示算法的过程:
https://www.naftaliharris.com/blog/visualizing-k-means-clustering/
二、K-means算法的优缺点:
@@优点:
@算法能根据较少的已知聚类样本的类别对树进行剪枝确定部分样本的分类;
@其次,为克服少量样本聚类的不准确性,该算法本身具有优化迭代功能,在已经求得的聚类上再次进行迭代修正剪枝确定部分样本的聚类,优化了初始监督学习样本分类不合理的地方;
@由于只是针对部分小样本可以降低总的聚类时间复杂度。
@对处理大数据集,该算法保持可伸缩性和高效性
@当簇接近高斯分布时,它的效果较好。
@@缺点:
@在 K-means 算法中 K 是事先给定的,这个 K 值的选定是非常难以估计的。很多时候,事先并不知道给定的数据集应该分成多少个类别才最合适;
@在 K-means 算法中,首先需要根据初始聚类中心来确定一个初始划分,然后对初始划分进行优化。这个初始聚类中心的选择对聚类结果有较大的影响,一旦初始值选择的不好,可能无法得到有效的聚类结果;
@该算法需要不断地进行样本分类调整,不断地计算调整后的新的聚类中心,因此当数据量非常大时,算法的时间开销是非常大的;
@若簇中含有异常点,将导致均值偏离严重(即:对噪声和孤立点数据敏感);
@不适用于发现非凸形状的簇或者大小差别很大的簇。
三、k-means的关键问题:
@K值的选取:
当你不知道待分类样本中有几类是,K值理论上可选区间为[1:X],即为样本的总数。可以通过穷举的方法选取K值,然后画出算法的代价函数值随着K值变化的曲线图,选择“肘点处”的值作为K的取值。如下图:
@目标函数:
用平方误差和(sum of the squared error, SSE)作为欧式空间的样本数据聚类的目标函数,同时也可以衡量不同聚类结果好坏的指标:
其中第一次for循环相当于算法的第3步;
其中第二次for循环相当于算法的第4步;
四、k-means面试问题:
@K-means中常用的到中心距离的度量有哪些?
@K-means中的k值如何选取?
@K-means算法中初始点的选择对最终结果有影响吗?
@K-means聚类中每个类别中心的初始点如何选择?
@K-means中空聚类的处理
@K-means是否会一直陷入选择质心的循环停不下来?
@如何快速收敛数据量超大的K-means?
@K-means算法的优点和缺点是什么?
@如何对K-means聚类效果进行评估?
@K-Means与KNN有什么区别?
引用文章(感谢这些机器学习分享者):
https://blog.csdn.net/weixin_38656890/article/details/80447548
https://blog.csdn.net/gaobellen/article/details/45024663
https://blog.csdn.net/u011204487/article/details/59624571
https://www.cnblogs.com/lianyingteng/p/7988779.html
https://blog.csdn.net/qq_33011855/article/details/81482511