决策树、Bagging、随机森林、Boosting、Adaboost、GBDT、XGBoost

决策树（Descision Tree）

决策树介绍

决策树基于“树”结构进行决策：
- 每个“内部节点”对应于某个属性上的测试
- 每个分枝对应于该测试的一种可能结果（即属性的某个取值）
- 每个叶节点对应于一个“预测结果”

决策树学习的三个步骤

• 特征选择
• 决策树的生成
• 决策树的修剪
  特征选择是决定用哪个特征来划分特征空间；
  特征选择的准则：信息增益或信息增益比

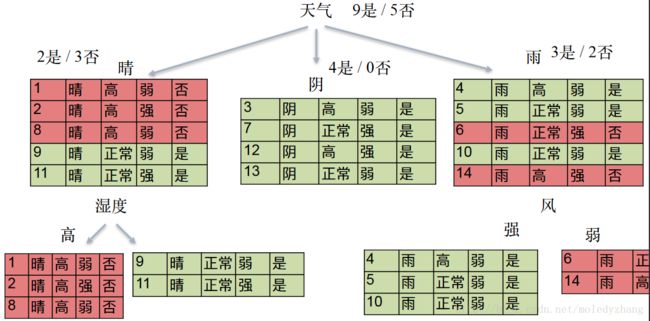
案例:预测小明今天出门打不打球

信息增益

熵

熵表示随机变量不确定性的度量
假设随机变量X，它可能属于n个类中的任何一个，通过样本的统计，它分别属于各个类的概率分别为p₁,p₂,…p_n，那么要想把某一样本进行归类所需要的熵就为：

H(X)=−∑i=1npilog2pi

若p _i=0,则0log0=0
注：熵只依赖与X的分布，与X的取值无关

条件熵

随机变量X给定的情况下随机变量Y的条件熵H(Y|X)，定义为

H(Y|X)=∑i=1npiH(Y|X=xi)

这里 pi=P(X=xi),i=1,2,...,n
当熵和条件熵中的概率由数据估计（特别是极大似然估计）得到时，所对应的熵与条件熵分别称为经验熵与经验条件熵。

信息增益

特征A对数据集D的信息增益g(D,A)定义为集合D的经验熵H(D)与特征A给定条件下D的经验条件熵之差，即

g(D,A)=H(D)−H(D,A)

小明打球案例中，数据集D的经验熵为：

H(D)=−914log2914−514log2514=0.940

特征天气对数据集D的信息增益为：

g(D,天气)=H(D)−[514H(D1)+414H(D2)+514H(D3)]

=0.940−[514(−25log225−35log235)+414(−44log244−04log204)+514(−35log235−25log225)]

=0.940−[5140.971+4140+5140.971]=0.940−0.694=0.246

其他特征对数据集D的信息增益的计算方法与之类似

信息增益比

以信息增益作为划分训练数据集的特征，存在偏向于选择取值较多的特征的问题。使用信息增益比可以对这一问题进行校正。
特征A对训练数据集D的信息增益比g_R(D,A)定义为其信息增益g(D,A)与训练数据集D关于特征A的值的熵H_A(D)之比，即

gR(D,A)=g(D,A)HA(D)

其中， HA(D)=−∑ni=1|Di||D|log2|Di||D| ，n是特征A取值的个数。

决策树生成算法

ID3

ID3的核心是使用信息增益准则选择特征，递归地构建决策树。

1）对当前样本集合，计算所有属性的信息增益；

2）选择信息增益最大的属性作为测试属性，把测试属性取值相同的样本划为同一个子样本集；

3）若子样本集的类别属性只含有单个属性，则分支为叶子节点，判断其属性值并标上相应的符号，然后返回调用处；否则对子样本集递归调用本算法。

ID3的bug：overfitting

可以把n个数据分成100%纯洁的n组，如编号

避免过拟合：没必要的分裂不要整，剪枝

C4.5

C4.5算法与ID3算法类似，使用信息增益比来选择特征

CART

CART使用基尼指数作为特征选择的准则，分类与回归树
样本集合D的基尼指数

Gini(D)=1−∑k=1K(|Ck||D|)2

特征A条件下集合D的基尼指数：

Gini(D,A)=|D1||D|Gini(D1)+|D2||D|Gini(D2)

其中，D ₂=D-D ₁

决策树算法总结

决策树的究极进化

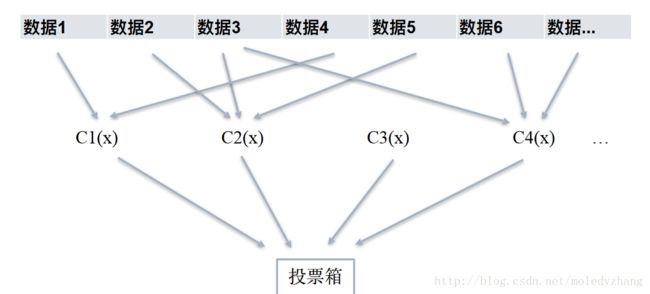
Bagging

Fit many large trees to bootstrap-resampled versions of the training data, and classify by majority vote.

Bagging的策略

（1）从样本集中重采样（有重复的）选出n个样本；

（2）在所有属性上，对这n个样本建立分类器（ID3、C4.5、CART、SVM、Logistic回归等）；

（3）重复以上两步m次，即获得了m个分类器；

（4）将数据放在这m个分类器上，最后根据这m个分类器的投票结果，决定数据属于哪一类。

注：其实Bagging采用了综合多个弱分类器的结果得到一个强分类器的思想；每个数看到部分数据，所有树看到全部数据。
m的取值为奇数。

Random Forest

Fancier version of bagging, add one more randomness in variable choosing.

随机森林在bagging基础上做了修改（有限样本，有限属性），基本思想为：

（1）从样本集中用Bootstrap采样（有放回的采样）选出n个样本（重采样）；

（2）从所有属性中随机选择k个属性，选择最佳分割属性作为节点建立CART决策树；

（3）重复以上两步m次，即建立了m棵CART决策树

（4）这m个CART形成随机森林，通过投票表决结果，决定数据属于哪一类

Boosting

Fit many large or small trees to re-weighted versions of the training data.
Classify by weighted majority vote.

Boosting是一族可将弱学习期提升为强学习器的算法（循环嵌套，不好的数据重新weight）。基本思想为：
（1）先在原数据集中长出一个tree
（2）把前一个tree没能完美分类的数据重新weight
（3）用新的re-weighted tree再训练出一个tree
（4）最终的分类结果由加权投票决定

Adaboost就是这类算法中最具代表性的一个算法。

Adaboost

Adaboost算法思路

• 步骤1 . 首先，初始化训练数据的权值分布。每一个训练样本最开始时都被 赋予相同的权值： 1/N
  
  D1=(w11,w12,...,w1i,...,w1N),w1i=1N,i=1,2,...,N

• 步骤2 . 进行多轮迭代，用m = 1,2, …, M表示迭代的第多少轮

  a.使用具有权值分布D_m的训练数据集学习，得到基本分类器（选取让误差率最低的阈值来设计基本分类器）
  

  Gm(x):χ→{−1,+1}

  b. 计算G_m(x)在训练数据集上的分类误差率
  

  em=P(Gm(xi)≠yi)=∑i=1NwmiI(Gm(xi)≠yi)
  
  Note: G_m(x)在训练数据集上的误差率e_m就是被G_m(x)误分类样本的权值之和。

  c. 计算Gm(x)的系数，a_m表示G_m(x)在最终分类器中的重要程度（目的：得到基本分类器在最终分类器中所占的权重）
  

  am=12log1−emem
  
  Note: e_m <= 1/2时，a_m >= 0，且a_m随着e_m的减小而增大，意味着分类误差率越小的基本分类器在最终分类器中的作用越大。

  d. 更新训练数据集的权值分布（为了得到样本的新的权值分布），用于下一轮迭代
  

  Dm+1=(wm+1,1,wm+1,2...wm+1,i...wm+1,N)
  
  
  wm+1,i=wmiZmexp(−αmyiGm(xi);),i=1,2,...,N
  
  使得被基本分类器G_m(x)误分类样本的权值增大，而被正确分类样本的权值减小。
  就这样，通过这样的方式，AdaBoost方法能“重点关注”或“聚焦于”那些较难分的样本上。
  其中，Z_m是规范化因子，使得D_m+1成为一个概率分布
  
  Zm=∑i=1Nexp(−αmyiGm(xi))

• 步骤3 .组合各个弱分类器
  
  f(x)=∑m=1MαmGm(x)
  
  从而得到最终分类器，如下：
  
  G(x)=sign(f(x))=sign(∑m=1MαmGm(x))

GBDT

a. Adaboost的Regression版本
Adaboost的Error计算

em=P(Gm(xi)≠yi)=∑i=1NwmiI(Gm(xi)≠yi)

GBDT的Error计算

em=P(Gm(xi),yi)=∑wmierr(Gm(xi),yi)

b. 把 残差作为下一轮的学习目标

比如: 用GBDT预测年龄
A的真实年龄是18岁，但第一棵树的预测年龄是12岁，差了6岁，即残差为6岁。那么在第二棵树里我们把A的年龄设为6岁去学习，如果第二棵树真的能把A分到6岁的叶子节点，那累加两棵树的结论就是A的真实年龄；如果第二棵树的结论是5岁，则A仍然存在1岁的残差，第三棵树里A的年龄就变成1岁，继续学。

c. 最终的结果有加权和值得到，不再是简单的多数投票

G(x)=∑αmGm(x)

XGBoost

XGBoost本质上还是GBDT，但是把速度和效率做到了极致，所以叫X (Extreme) GBoosted
特点：
a. 使用L1 L2 Regularization 防止Overfitting

b. 对代价函数一阶和二阶求导，更快的Converge

c. 树长全后再从底部向上减枝，防止算法贪婪