排序算法总结

冒泡排序

• 一种简单直观的排序算法，时间复杂度$O(n^2)$，属于稳定排序和就地排序
• 遍历未排序的元素，比较相邻的元素，每次找出最大值放在队尾

def bubble_sort(nums):
    for i in range(1, len(nums)):
        for j in range(len(nums) - i):
            if nums[j] > nums[j+1]:
                nums[j], nums[j+1] = nums[j+1], nums[j]

冒泡排序有一种优化算法，在外层循环立一个flag，如果内层循环没有发生交换，说明数组已经有序，停止遍历。

---

选择排序

• 与冒泡排序类似，时间复杂度$O(n^2)$，属于不稳定排序和就地排序
• 首先在未排序序列中找到最小元素，存放到序列的起始位置
• 再从剩余未排序元素中继续寻找最小元素，然后放到已排序序列的末尾
• 交换次数远少于冒泡排序

def select_sort(nums):
    for i in range(len(nums)-1):
        # 最小数的索引
        min_index = i
        for j in range(i+1, len(nums)):
            if nums[j] < nums[min_index]:
                min_index = j
        if min_index != i:
            nums[i], nums[min_index] = nums[min_index], nums[i]

稳定排序要求不改变相等元素的相对位置，而选择排序选出最小元素，和前面的元素交换位置，可能会打乱相等元素的顺序。

---

插入排序

• 时间复杂度$O(n^2)$，属于稳定排序和就地排序
• 类比打扑克牌理牌的过程，从前向后遍历，把当前元素插入合适的位置（初始元素默认是排好的），路过的元素全部后移一位

def insert_sort(nums):
    for i in range(1, len(nums)):
        cur = nums[i]  # 保存当前元素
        j = i - 1
        while j >= 0 and nums[j] > cur:
            nums[j+1] = nums[j]
            j -= 1
        nums[j+1] = cur

插入排序在对几乎已经排好序的数据操作时，效率高，即可以达到线性排序的效率。

---

快速排序

• 处理大数据最快的排序算法，python内置的sort()用的就是快速排序
• 时间复杂度$O(n\cdot log(n))$，属于不稳定排序和就地排序
• 本质上可以看作递归分治的冒泡排序

算法步骤：

1. 从数组中选定一个基准值
2. 将所有比基准值小的元素放在基准值的左边，比基准值大的放在序列的右边
3. 递归地对左右两个子数组排序（继续选基准值，划分区间）

以左指针作为基准值为例：

def quick_sort(nums, l, r):
    if l >= r:
        return

    i, j = l, r
    while i < j:
        while i < j and nums[j] >= nums[l]:
            j -= 1
        while i < j and nums[i] <= nums[l]:
            i += 1
        nums[i], nums[j] = nums[j], nums[i]
        
    nums[i], nums[l] = nums[l], nums[i]
    quick_sort(nums, l, i - 1)
    quick_sort(nums, i + 1, r)

• 最后i, j 一定相等,nums[i], nums[l] = nums[l], nums[i]中的 i 换成 j 也可
• 这里选定的左指针做基准值，所以先遍历右边，再遍历左边，i,j的顺序不能颠倒

快速排序划分区间，可能将相等的值划分到不同的区间，所以不稳定。

---

计数排序

• 计数排序的核心是将数组的值作为键，频率作为值，映射到额外开辟的数组空间中
• 当输入的元素是 n 个 0 到 k 之间的整数时，时间复杂度为$O(n+k)$，是稳定排序和非就地排序

算法步骤：

• 创建一个能装下所有数字的数组bucket
• 统计原始数组nums中每个元素出现的次数，存入bucket
• 遍历bucket，将每个元素放在新数组的第0，1，2，……位置，每放一个元素x，bucket[x]减去1

def count_sort(nums, max_value):
    # 0 <= nums[i] <= max_value
    bucket_len = max_value + 1
    bucket = [0] * bucket_len
    for x in nums:
        bucket[x] += 1
    index = 0
    for i in range(bucket_len):
        while bucket[i] > 0:
            nums[index] = i
            index += 1
            bucket[i] -= 1
    return nums

计数排序是用来排序0到100之间的数字的最好的算法，属于牺牲空间换时间了

---

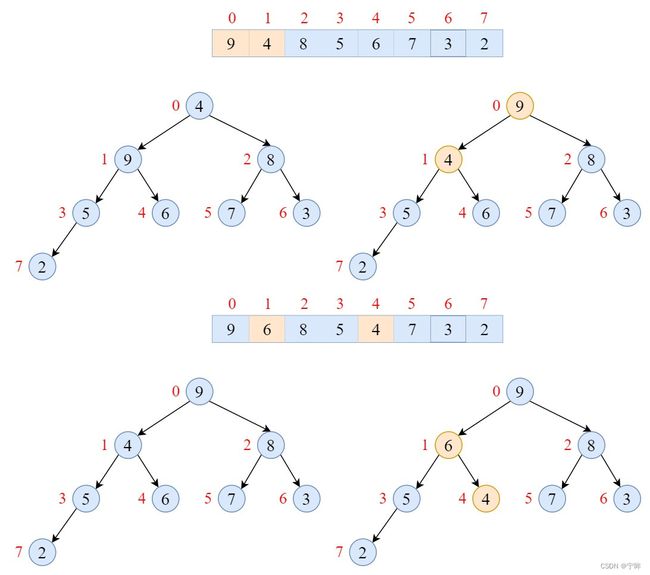
堆排序

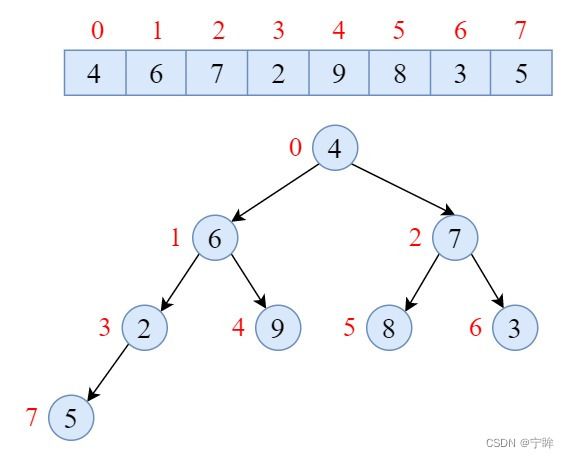
原始数组：[4, 6, 7, 2, 9, 8, 3, 5]

• 堆是一颗完全二叉树，父节点大于左右子节点

• 除根节点外，节点k的父节点是k // 2 - 1，左右子节点是2k + 1和2k + 2

• 从下往上构建堆，保证根节点是最大值，每次更新节点，都需要递归的维护下层树

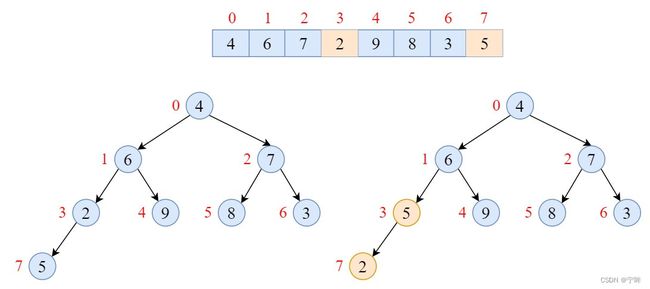
从下往上构建堆：

---

---

---

---

至此，二叉树形成一个完整最大堆，每个节点都不小于其左右子节点

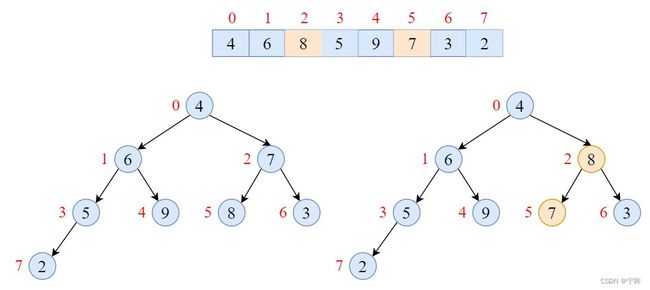
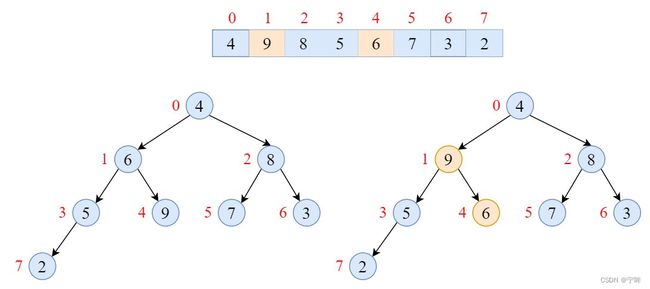
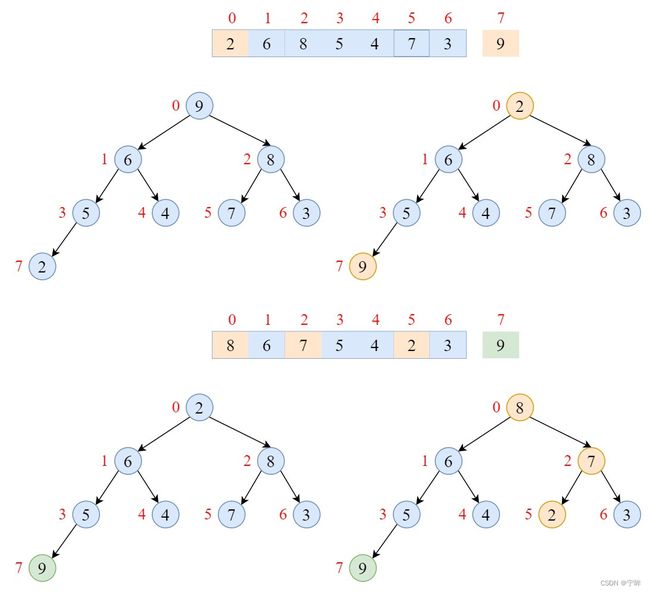
那么，如何用最大堆进行排序呢？

答案是每次将根节点（堆首，最大值）与最后一个叶子节点（堆尾）交换，然后缩小堆的尺寸，更新堆，直到堆的尺寸为1

以弹出根节点（9）为例：

---

下面堆排序的代码：

自己造轮子（最大堆）

class Solution(object):
    def heap_sort(self, nums):
        l = len(nums)
        # 构造大顶堆，从非叶子节点开始倒序遍历，因此是l//2 -1 就是最后一个非叶子节点
        for i in range(l // 2 - 1, -1, -1):
            self.build_heap(nums, i, l)
        # 交换根节点与最后一个叶子节点，缩小堆的尺寸后更新堆
        for i in range(l-1, -1, -1):
            # nums[0]是最大值
            nums[0], nums[i] = nums[i], nums[0]
            self.build_heap(nums, 0, i)
        return nums

    def build_heap(self, nums, i, l):
        """构建大顶堆"""
        # 左右子节点的下标
        left, right = 2 * i + 1, 2 * i + 2

        index = i
        # 在当前节点和左右子节点找最大值
        if left < l and nums[index] < nums[left]:
            index = left
        if right < l and nums[index] < nums[right]:
            index = right

        if i != index:  # 如果发生交换，递归维护
            nums[index], nums[i] = nums[i], nums[index]
            self.build_heap(nums, index, l)
        return nums

调用内置的heapq

import heapq

def heap_sort(nums):
    heapq.heapify(nums)
    res = []
    for _ in range(len(nums)):
        res.append(heapq.heappop(nums))
    return res

堆排序属于不稳定排序和就地排序，如果有两个相等的数，有着不同的父节点，一个父节点发生交换，另一个不交换，两个相等数的顺序就发生了改变。