图神经网络（8）- 如何应用GNN

目录

Augment Graphs

图的特征增强

condition 1：输入的图没有节点特征（可能只有邻接矩阵

solution：

condition 2：特殊图结构,GNN很难学

solution

图的结构增强

condition1：图过于稀疏，信息传递效率低——增强稀疏图

solution：

condition2：图过于密集，信息传递开销大

solution：节点邻居采样

condition3：图过于大，计算图太大了，数据量大

图的训练过程

GNN的预测头**(重要）

GNN的监督学习与无监督学习

GNN的损失函数

GNN的评估矩阵

GNN数据集的划分**(重要）

condition 1： 节点分类任务

solution 1：

solution2 ：

condition 2：边连接预测任务

solution1：

solution2：

---

摘要： 图的特征增强，图的结构增强，GNN训练过程中的处理和数据集的划分（transductive和inductive法就是跟数据集划分相关）

Augment Graphs

在介绍图神经网络时，我们假定认为计算图就是原始的图，但是实际应用中我们很少使用原始图。因为，在实际中，a.得到的图并不是完全符合模型的要求，b.就算符合要求增强得到的效果也更好。

增强图分为两个方面：图的特征增强与图的结构增强

图的特征增强

图的特征增强，主要是因为图的特征过少，导致最后模型的实现结果不佳。下面分情况分析。

condition 1：输入的图没有节点特征（可能只有邻接矩阵

solution：

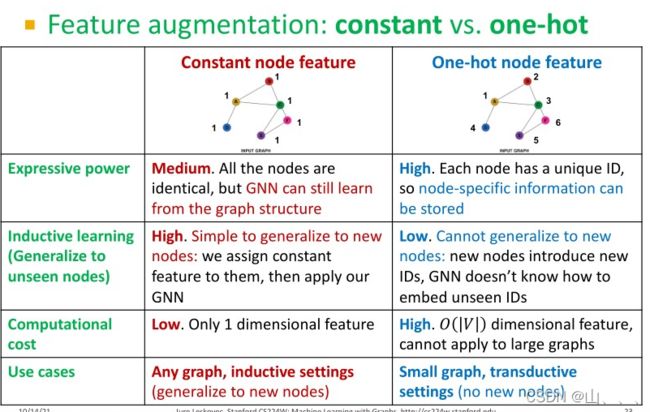
                  a. 给节点分配相同的实数值做特征。

                  b. 给节点分配ID值（可以用one-hot的方式）做特征。

两种方法的比较：

condition 2：特殊图结构,GNN很难学

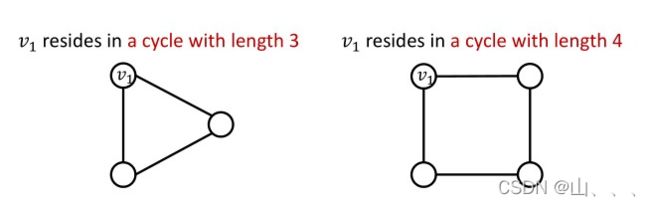
例如GNN学不会，V1所在环的长度，区分不了下面两种情况！！Jure Leskovec给出的原因是图里面所有点都是度为2，所以这两个图的计算图是一样的二叉树。我没完全理解这个意思。

solution

        增加一个节点特征用来表示这个环的长度，如果是其他情况，就增加节点特征表示其他——这个思路就是，如果GNN从图结构学不会这个特征，那么我们就把它加到节点特征里，让GNN从节点特征学。（GNN的学习经验来源就是节点特征+图结构）

其他常用增强特征：节点度，聚集系数，PageRank，centrality（参考————有空再补）

图的结构增强

图的结构增强有三种情况，分别是图过于稀疏，图过于密集以及图过于大。每一种情况中，由于图的结构问题，都会带来实际使用中的问题。

condition1：图过于稀疏，信息传递效率低——增强稀疏图

solution：

a. 增加虚拟边

b.增加虚拟点——虚拟点连接所有边

condition2：图过于密集，信息传递开销大

solution：节点邻居采样

有兴趣可以看这篇论文。

Hamilton et al. Inductive Representation Learning on Large Graphs, NeurIPS 2017

具体操作就是：例如求A的embedding，在GNN的每一层，A的邻居都是采样获得，不是所有的邻居。

优点：1.极大的减少了计算代价，

           2.Allows for scaling to large graphs (more about this later)

condition3：图过于大，计算图太大了，数据量大

        Will cover later in lecture: Scaling up GNNs（后面补参考链接）

图的训练过程

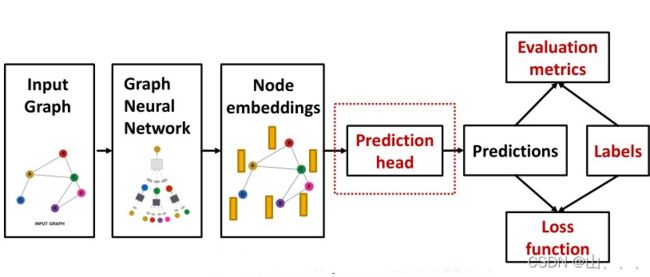
下面是完成一个GNN task的流程模板：

 可以看出来，前面的GNN就是得到节点embeddings，后面的大致流程其实就和普通的NN一样。当然也有GNN很特殊的地方。

GNN的预测头**(重要）

对于GNN得到的节点embeddings，在处理不同层级的任务时，处理方式不同。

节点任务：不需要什么太多的处理，直接把embeddings当作线性回归或者逻辑回归模型的输入就行。

 边任务：两种处理方式：1. Concatenation + Linear 2. Dot product

                有一个需要注意的小知识点，就是维度的要求。

 图任务：需要把所有的节点embeddings聚合到一起，作为图embedding。

聚合一般采用下面的这些全局池化操作

 这些操作对于小的图效果很好。但是池化操作太简略，对于有些结构不能区分。例如：

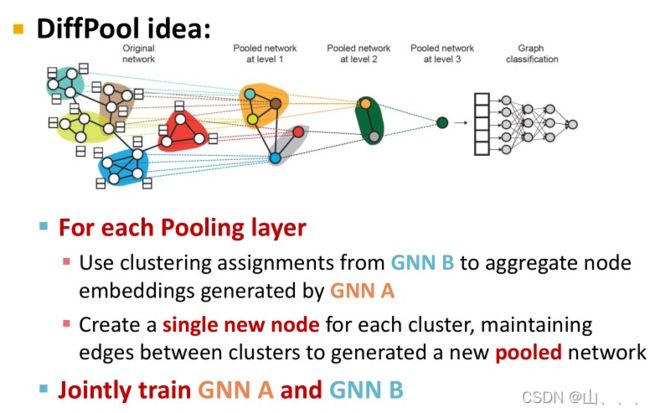
 这个时候引入更为复杂的hierarchically global pooling。这种池化的思路很简单，就是全局池化的时候，不是所有点一起，而是把点分成几部分，每个部分进行全局池化，最后的结果再来一次全局池化。

在实际操作中，可以用一个GNN来计算怎么把点分成几部分，另外GNN一个用来计算图中节点embeddings。这两个GNN可以并行执行，在预测头这个位置合二为一，并且可以通用反向传播同时优化两个GNN。

GNN的监督学习与无监督学习

对图神经网络而言，监督学习就是利用外部提供的label来训练，无监督学习就是利用图本身的结构关系进行训练。所以可以说，在无监督学习里面，也相当于是有label的，只是说这个label是图自身产生的。譬如说，图有连接，有聚集系数等等特征。

GNN的损失函数

这一部分没什么特别的，就和其他神经网络差不多。分类任务就常用交叉熵损失函数，回归任务就常用均方误差。

GNN的评估矩阵

和其他神经网络同。略，之后有时间补吴恩达关于评估模型的一些知识点。

GNN数据集的划分**(重要）

GNN数据集的划分有一些与众不同之处。一般来讲，当我们训练模型时，我们会把数据分为：训练集（约60%）、验证集（20%）、测试集（20）。训练集用来训练模型，验证集用来选择超参数，测试集用来评估模型好坏。并且，有一个非常重要的注意点：各个数据集的数据要独立同分布。在GNN里面，我们也想这么划分。但是在一些特殊情况下，很难实现所谓独立同分布。

图分类任务的数据集划分是可以达到独立同分布的。

下面介绍一些特殊情况并介绍怎么处理。

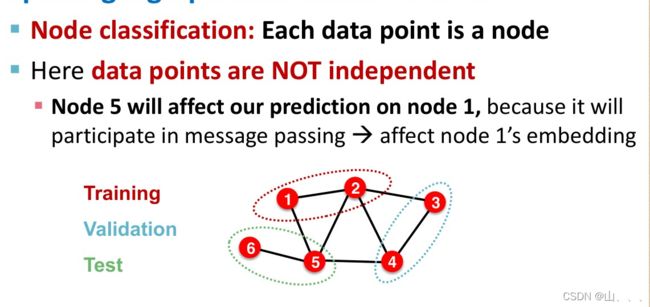
condition 1： 节点分类任务

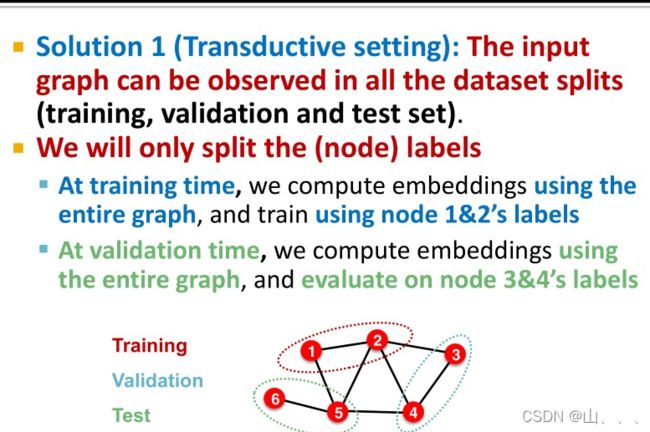
solution 1：

所有的节点参与embeddings的计算，但是在训练时只使用训练集中的节点。具体一点讲呢，就是只有所有点都通过GNN得到了embeddings，但是在计算loss，和反向传播时，只用训练集中的数据，相当于只划分了label。——transductive（直推法）

solution2 ：

直接把点划分为三个数据集，三个数据集之间存在的边都去掉，相当于把一个图划分会三个图，一个图是一个数据集。——inductive（归纳法）

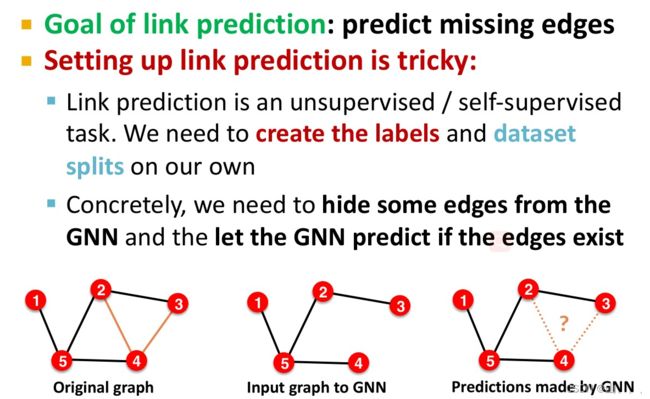
condition 2：边连接预测任务

先介绍一下，边连接预测任务。

把输入到GNN的边记作信息边，用来当label的边记作监督边。这样的话，原始图中就有了两类边。

solution1：

假设我们有三个图的数据，每个图分别用作训练集、验证集、测试集。——inductive（归纳法）

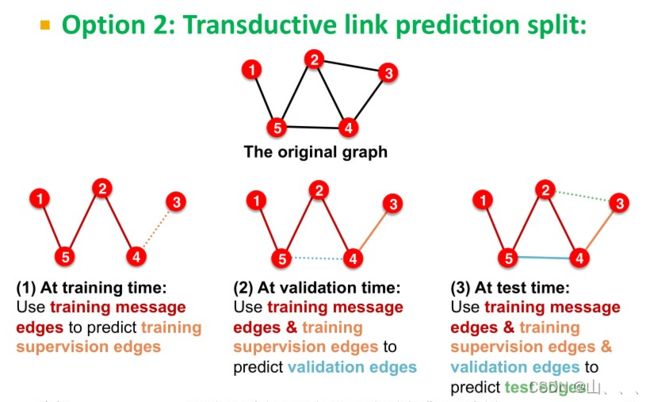
solution2：

只有一个图的数据，我们把这个图的边分成四类。用信息边和监督边训练GNN模型，然后用这个GNN模型输入包括信息边和监督边，来预测验证边，然后用这个GNN模型输入包括信息边、监督边、和验证边，来预测测试边。——transductive（直推法）

 DeepSNAP 提供了GNN流程中的核心模块

GraphGym 设计GNN