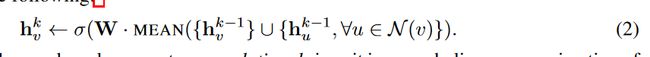3网络连接图_CS224w 图神经网络(Graph Neural Networks)
Hi,大家好,这里是居家隔离的糖葫芦喵喵~!
在之前的内容里我们讨论了图像和自然语言的机器学习方法以及简单的强化学习方法,今天开始我们要接触到机器学习的另一个有趣的领域——图机器学习。下面为大家带来斯坦福图机器学习CS224w 2019的Assginment 2的解析,还请大家多多指教~!
Part 0 CS224n Assignment简介与环境准备
1 课程简介
课程页面:CS224W | Home
课程视频[英字]:
【油管英字】CS224w 斯坦福图网络机器学习2019_哔哩哔哩 (゜-゜)つロ 干杯~-bilibiliwww.bilibili.com本门课程原来叫Analysis of Networks,也就是传统的网络分析,19年秋季改名为Machine Learning with Graphs,可见GNN等一系列方法对传统网络分析研究的推动。19年秋季课程除了传统网络分析涵盖的网络特征(度、直径、聚集系数、模块度等)、网络模型(随机网络、小世界等)、社团发现、网络连接分析(PageRank)、网络传染模型(SIR)等,全新加入了图神经网络(Graph Neural Networks)相关内容,受到了广大炼丹爱好者的高度评价(笑)。关于网络分析的理论与作业内容这里就不再赘述,感兴趣的炼丹爱好者们可以根据视频内容进行进一步研究,这里我们只结合Assignment 2对图神经网络的理论与实践进行详细介绍。
那么,让我们愉悦地开始研究GNN吧!
2. 环境准备
本次课程使用的工具是PyTorch Geometric (PyG):
rusty1s/pytorch_geometricgithub.com文档:PyTorch Geometric Documentation
PyTorch Geometric (PyG)是一款非常好用的PyTorch图神经网络的扩展包。它囊括了很多主要的图卷积的实现方式,如果你熟悉PyTorch的话,那将非常容易上手。不过安装稍显麻烦。
基本环境:Linux/gcc 5.0+/PyTorch 1.4.0 (支持CUDA9.2/10/10.1)
Linux下关于gcc的版本问题,建议使用安装SCL源之后安装devtoolset即可。
升级到gcc 5.2:
wget https://copr.fedoraproject.org/coprs/hhorak/devtoolset-4-rebuild-bootstrap/repo/epel-6/hhorak-devtoolset-4-rebuild-bootstrap-epel-6.repo -O /etc/yum.repos.d/devtoolset-4.repo
yum install devtoolset-4-gcc devtoolset-4-gcc-c++ devtoolset-4-binutils -y
scl enable devtoolset-4 bash首先要安装torch-scatter/torch-sparse/torch-spline-conv/torch-cluster:
pip install torch-scatter==latest+${CUDA} -f https://pytorch-geometric.com/whl/torch-1.4.0.html
pip install torch-sparse==latest+${CUDA} -f https://pytorch-geometric.com/whl/torch-1.4.0.html
pip install torch-cluster==latest+${CUDA} -f https://pytorch-geometric.com/whl/torch-1.4.0.html
pip install torch-spline-conv==latest+${CUDA} -f https://pytorch-geometric.com/whl/torch-1.4.0.html如果速度太慢建议通过 http://pytorch-geometric.com/whl/torch-1.4.0.html 下载对应的whl后pip install。
然后pip install即可:
pip install torch-geometricimport的时候可能出现的问题:version `GLIBCXX_3.4.21' not found:是因为升级gcc时新的动态库没有替换老版本gcc的动态库,重新做软连接即可:CSDN-专业IT技术社区-登录
导入成功!复杂的环境配置完毕,可以尝试运行pytorch_geometric/examples/下的demo看看有没有问题。
Part 1 PyG 数据格式
PyG定义了一套自己的数据格式,主要用来描述图,以及加载数据,整体结构与pytorch的处理方式非常接近。
1 torch_geometric.data 图数据结构
class Data(x=None, edge_index=None, edge_attr=None, y=None, pos=None, norm=None, face=None, **kwargs)主要参数:
- x [num_nodes, num_node_features] node的特征
- edge_index [2, num_edges] 由节点编号(0开始)对构成的edge,第一行是source,第二行是target
- edge_attr [num_edges, num_edge_features] edge的特征
- y: label
简单构造一个Data实例:
from torch_geometric.data import Data
x = torch.tensor([[2,1],[5,6],[3,7],[12,0]],dtype=torch.float)
y = torch.tensor([0,1,0,1], dtype=torch.float)
edge_index = torch.tensor([[0,1,2,0,3],
[1,0,1,3,2]],dtype=torch.long)
mydata = Data(x=x,y=y,edge_index=edge_index)
mydata
# 输出: Data(edge_index=[2, 5], x=[4, 2], y=[4])这样我们就用Data简单表示了一张由4个点5条边构成的图。
2. torch_geometric.datasets 数据加载
PyG提供了大量的benchmark数据集的载入方式,下面分别以Cora和ENZYMES数据集为例加载。
2.1 Cora
Cora = Planetoid(root='/tmp/Cora', name='Cora')
Cora[0]
# 输出: Data(edge_index=[2, 10556], test_mask=[2708], train_mask=[2708], val_mask=[2708], x=[2708, 1433], y=[2708])
np.unique(Cora[0].y)
# 输出: array([0, 1, 2, 3, 4, 5, 6])
sum(Cora[0].test_mask)
# 输出: tensor(1000)
sum(Cora[0].train_mask)
# 输出: tensor(140)可以看到Cora是一个单张图构成的节点7分类数据集,它有2708个点,10556/2条边,每个点初始1433维特征。训练数据train_mask指定,共140个节点,测试数据test_mask指定,共1000各节点。
2.2 ENZYMES
ENZYMES = TUDataset(root='/tmp/ENZYMES', name='ENZYMES')
len(ENZYMES)
# 输出: 600
y = []
for e in ENZYMES:
y.append(e.y)
np.unique(y)
# 输出: array([0, 1, 2, 3, 4, 5])而ENZYMES则是600张图构成的图6分类数据集。
然后我们用DataLoader再观察一下:
ENZYMESloader = DataLoader(ENZYMES[:int(len(ENZYMES) * 0.8)], batch_size=32, shuffle=True)
for batch in ENZYMESloader:
batch
print(batch, batch.num_graphs)
# 输出: Batch(batch=[971], edge_index=[2, 3518], x=[971, 3], y=[32]) 32我们加载了600*0.8=480张图,每个batch32张共15batch,最后一个batch有32张图,共计971个节点,3518条边。
batch.batch
# 输出: tensor([ 0, 0, 0, ..., 31, 31, 31])batch变量用于指示每个节点属于batch中的第几个graph。
有了上述几个基本内容我们就可以方便地配合PyTorch准备模型输入的数据了。
下面我们开始构造模型。
Part 2 GNN基本理论与PyG消息传递机制
1. GNN基本理论
简单来说图神经网络主要是靠图卷积操作来完成的。而图卷积操作是一种将目标节点周围邻居节点的信息进行聚合的一种方法:
于是,根据这个公式,我们要做的就变成了三件事:
- A. 邻居信息的变换:
- B. 邻居信息聚合:
- C. 自己的信息与聚合后的邻居信息的变换:
在PyG中,这个流程被对应到self.propagate这个操作中,self.propagate将分别执行上述三件事:
- A. 执行self.message,对应公式中
,即邻居信息的变换
- B. 执行self.aggregate,对应公式中
,即邻居信息聚合
- C. 执行self.update,对应公式中
,即自己的信息与聚合后的邻居信息的变换
这样我们就好理解了,上述公式将被拆成三个部分写进对应的方法。下面我们分别从GCN/GraphSage/GAT来具体实践一下!
2. GCN
其实GCN很简单,只不过这个公式和消息传递公式对比起来比较迷惑。
简单来看:
便于理解我们采用另一种形式的公式:
归一化系数计算对应
- A. self.message:
计算归一化系数
- B. self.aggregate:
,选择add
- C. self.update:
(无)
class GCNConv(MessagePassing):
def __init__(self, in_channels, out_channels):
super(GCNConv, self).__init__(aggr='add') # /space 选择聚合方法
self.lin = torch.nn.Linear(in_channels, out_channels)
def forward(self, x, edge_index):
# 添加自环
edge_index, _ = add_self_loops(edge_index, num_nodes=x.size(0))
# /theta 初始特征的一次变换
x = self.lin(x)
return self.propagate(edge_index, size=(x.size(0), x.size(0)), x=x)
def message(self, x_j, edge_index, size):
# /phi 计算归一化系数
row, col = edge_index
deg = pyg_utils.degree(row, size[0], dtype=x_j.dtype)
deg_inv_sqrt = deg.pow(-0.5)
norm = deg_inv_sqrt[row] * deg_inv_sqrt[col]
return norm.view(-1, 1) * x_j
def update(self, aggr_out):
# /gamma 无
return aggr_out3. GraphSage
GraphSage其实有两个贡献,一是提出了更多的聚合方法(mean/lstm/pooling),二是对邻居信息进行多跳抽样(我们将在下一节中讨论)。那么最一般GraphSage的聚合形式是mean(好像目前只支持add/mean/max)。
回来看公式:
- A. self.message:没有
不做变换
- B. self.aggregate:
,选择mean
- C. self.update:
其实是第二行,要结合GraphSage论文看更明白,见下图第五行:
其实就是拼接再线性变换。
class GraphSage(pyg_nn.MessagePassing):
"""Non-minibatch version of GraphSage."""
def __init__(self, in_channels, out_channels, reducer='mean',
normalize_embedding=True):
super(GraphSage, self).__init__(aggr='mean') # /space 选择聚合方法
if normalize_embedding:
self.normalize_emb = True
def forward(self, x, edge_index):
num_nodes = x.size(0)
return self.propagate(edge_index, size=(num_nodes, num_nodes), x=x)
def message(self, x_j, edge_index, size):
# /phi 无
return x_j
def update(self, aggr_out, x):
# /gamma 拼接再线性变换
concat_out = torch.cat((x, aggr_out), 1)
aggr_out = F.relu(self.agg_lin(concat_out))
if self.normalize_emb:
aggr_out = F.normalize(aggr_out, p=2, dim=1)
return aggr_out搞定!
我们注意到论文里还有一个公式:
类似先拼接再聚合,论文中有详细实验对比。
4. GAT
我们都很熟悉attention了,其实就是加权,为此需要通过上下文来计算加权系数。而multi-head只不过是在channel上进行切分分别计算最后拼接/平均而已。
依旧分析公式,有
- A. self.message:
就是计算att加权系数,这里是将目标节点和邻居节点信息进行拼接后进行变换,归一化。
- B. self.aggregate:
,选择add
- C. self.update:
(无)
class GAT(pyg_nn.MessagePassing):
def __init__(self, in_channels, out_channels, num_heads=1, concat=True,
dropout=0, bias=True, **kwargs):
super(GAT, self).__init__(aggr='add', **kwargs)
self.in_channels = in_channels
self.out_channels = int(out_channels / num_heads)
self.heads = num_heads
self.concat = concat
self.dropout = dropout
self.lin = nn.Linear(in_channels, self.out_channels * num_heads) # TODO
self.att = nn.Parameter(torch.Tensor(1, self.heads, self.out_channels * 2)) # TODO
if bias and concat:
self.bias = nn.Parameter(torch.Tensor(self.heads * self.out_channels))
elif bias and not concat:
self.bias = nn.Parameter(torch.Tensor(self.out_channels))
else:
self.register_parameter('bias', None)
nn.init.xavier_uniform_(self.att)
nn.init.zeros_(self.bias)
def forward(self, x, edge_index, size=None):
if size is None and torch.is_tensor(x):
edge_index, _ = remove_self_loops(edge_index)
edge_index, _ = add_self_loops(edge_index, num_nodes=x.size(0))
# /theta 初始特征的一次变换
x = self.lin(x)
return self.propagate(edge_index, size=size, x=x)
def message(self, edge_index_i, x_i, x_j, size_i):
# /phi 计算att系数
x_i = x_i.view(-1, self.heads, self.out_channels)
x_j = x_j.view(-1, self.heads, self.out_channels)
alpha = (torch.cat([x_i, x_j], dim=-1) * self.att).sum(dim=-1)
alpha = F.leaky_relu(alpha, 0.2)
alpha = pyg_utils.softmax(alpha, edge_index_i, size_i)
alpha = F.dropout(alpha, p=self.dropout, training=self.training)
return x_j * alpha.view(-1, self.heads, 1)
def update(self, aggr_out):
# /gamma multi-head恢复
if self.concat is True:
aggr_out = aggr_out.view(-1, self.heads * self.out_channels)
else:
aggr_out = aggr_out.mean(dim=1)
if self.bias is not None:
aggr_out = aggr_out + self.bias
return aggr_out搞定!
Part 3 GraphSage NeighborSampler
前面提及GraphSage有两个贡献,这里我们来讨论对邻居信息进行多跳抽样的实现:
NeighborSampler!
NeighborSampler(data, size, num_hops, batch_size=1, shuffle=False, drop_last=False, bipartite=True, add_self_loops=False, flow='source_to_target')该方法返回一个生成器,主要需要的参数有data数据、采样邻居数(或比例)、采样跳数、bs等。其中bipartite参数指定返回的数据形式:
- bipartite=True 返回DataFlow 数据形式
- bipartite=False 返回Data 数据形式(实际上是Data形式的subgraph)
在 https://github.com/rusty1s/pytorch_geometric/blob/a8f32aaff8608e497f112f700d1fd8ca0cb9ae18/test/data/test_sampler.py 中我们可以看到两种方法的使用例子。
1. bipartite
Neighborloader = NeighborSampler(Cora[0], size=[25, 10], num_hops=2, batch_size=1,
shuffle=True, add_self_loops=True,)
for ner in Neighborloader(Cora[0].train_mask):
print(ner)
# 输出: DataFlow(1<-4<-9)即 layer 0有9个点,layer 1有4个点,layer 2有1个点(目标)
hoop设置两跳,ner里于是有了两个Block数据:、
ner[0], ner[1]
# 输出: Block(n_id=[9], res_n_id=[4], e_id=None, edge_index=[2, 18], size=[2]),
# Block(n_id=[4], res_n_id=[1], e_id=None, edge_index=[2, 4], size=[2]))- n_id是二分图中节点(从0开始)到原图的id映射
- res_n_id是二分图中向其他层连接的节点id
- edge_index二分图中的边
具体来看:
ner[0].n_id, ner[0].res_n_id
# 输出: (tensor([ 109, 2481, 234, 826, 2287, 114, 2506, 610, 2288]),
tensor([5, 8, 7, 6]),也就是说这一层ner[0] 26个节点编号:[ 109, 2481, 234, 826, 2287, 114, 2506, 610, 2288]
其中第[5, 8, 7, 6](即[ 114, 2288, 610, 2506])是和下一层ner[1] 相连接的:
ner[1].n_id, ner[1].res_n_id
# 输出:(tensor([ 114, 2288, 610, 2506]),
tensor([0]),batch>1时也就是采样一个包含batch个目标点的二分图。
因此我们在训练时要先输入layer 0进行训练,然后再此基础上对layer 1进行训练,最终得到layer 1的res_n_id的输出。
def forward_data_flow(self, x, edge_weight, data_flow):
block = data_flow[0]
weight = None if block.e_id is None else edge_weight[block.e_id]
x = relu(
self.conv1((x, None), block.edge_index, weight, block.size))
block = data_flow[1]
weight = None if block.e_id is None else edge_weight[block.e_id]
x = relu(
self.conv2((x, None), block.edge_index, weight, block.size))
return x2. subgraph
subgraph模型上与不使用NeighborSampler的无异,唯一区别是Data中的变量:
ner
# 输出:Data(b_id=[1], e_id=[20], edge_index=[2, 20], n_id=[19], sub_b_id=[1])
ner.b_id, ner.sub_b_id, ner.n_id
# 输出:(tensor([100]),
tensor([18]),
tensor([ 95, 2073, 2054, 6, 2074, 2072, 315, 2576, 1416, 734, 2311, 1628,
1841, 1680, 408, 2056, 1602, 1204, 100]))- n_id是子图中节点(从0开始)到原图的id映射
- b_id是目标点
- sub_b_id是子图中目标点的id
batch>1时也就是采样一个包含batch个目标点的子图。
我们在训练时放入采样的子图,只取目标点sub_b_id作为模型输出即可,其他不变。
out = model(data.x[subdata.n_id], subdata.edge_index, weight)
out = out[subdata.sub_b_id]Part 4 实验
1. Cora
Cora:一个单张图构成的节点7分类数据集,它有2708个点,10556/2条边,每个点初始1433维特征。训练数据train_mask指定,共140个节点,测试数据test_mask指定,共1000各节点。本质是一个transductive learning的问题。
hidden_dim=64 dropout=0.6 lr=0.001 batch_size=32 epoch=200 adam优化器
GCN:采用GCN-ReLU-Dropout-GCN-ReLU-Dropout结构
GAT:采用GAT(head=8)-ELU-Dropout-GAT(head=1)-ELU-Dropout结构
GraphSage:采用GraphSage-ReLU-Dropout-GraphSage-ReLU-Dropout-Linear结构
评测:由于训练数据较少,结果并不稳定,这里简单取了10次试验最高分数(基本接近论文中水平):
GCN:0.815 GAT:0.825 GraphSage:0.795
2.ENZYMES
ENZYMES:是600张图构成的图6分类数据集。本质是一个inductive learning的问题。
图分类和节点分类的差别仅在于最后需要对全图节点进行global_mean_pool,以得到图的表示向量。
hidden_dim=64 dropout=0 lr=0.001 batch_size=32 epoch=500 adam优化器
GCN:采用GCN-ReLU-Dropout-GCN-ReLU-Dropout-Linear结构
GAT:采用GAT(head=8)-ELU-Dropout-GAT(head=1)-ELU-Dropout结构
GraphSage:采用GraphSage-ReLU-Dropout-GraphSage-ReLU-Dropout-Linear结构
评测:
GCN:0.38 GAT:0.36 GraphSage:0.73
感兴趣的同学们可以继续炼丹!
Browse the State-of-the-Art in Machine Learningpaperswithcode.com在这个网站上可以看到一些经典数据集的分数榜,有兴趣的同学可以刷一下。
本次内容中我们结合PyTorch Geometric (PyG),研究了图神经网络消息传递机制与实现方法,并分别实现了GCN/GAT/GraphSage。近年来随着图神经网络技术的发展,很多领域都在尝试引入这种新的方法:如通过推荐系统中天然具有的链接关系构成二分图;又如自然语言处理中通过构造句子语法树来获得图等。相信随着计算力与算法的进一步提升,在更多的问题中都能够运用到这种方法,让我们一起期待新技术的到来吧!
では、おやすみ~!