皮尔逊相关性分析一文详解+python实例代码
目录
前言
一、数值类型
二、皮尔逊系数使用场景
二、皮尔逊相关系数(Pearson correlation)
1.定义
2.线性关系判定
3.正态检验
1.KS检验
4.计算代码
点关注,防走丢,如有纰漏之处,请留言指教,非常感谢
参阅
前言
相关性分析算是很多算法以及建模的基础知识之一了,十分经典。关于许多特征关联关系以及相关趋势都可以利用相关性分析计算表达。其中常见的相关性系数就有三种:person相关系数,spearman相关系数,Kendall's tau-b等级相关系数。各有各自的用法和使用场景。当然关于这以上三种相关系数的计算算法和原理+代码我都会在我专栏里面写齐全。目前关于数学建模的专栏已经将传统的机器学习预测算法、维度算法、时序预测算法和权重算法写的七七八八了,有这个需求兴趣的同学可以去看看。
一、数值类型
之前在我上篇文章说过关于数据特征是一个很重要的例子,任何分析算法都需要建立在其符合使用场景之上,我们需要对症下药,从数据特征开始分析。
按照数据存储的数据格式可以归纳为两类:
按照特征数据含义又可分为:
- 离散型随机变量:取值只能是可取范围内的指定数值类型的随机变量,比如年龄、车流量此类数据。
- 连续随机变量:按照测量或者计算方法得到,在某个范围内连取n个值,此类数据可化为定类数据。
- 二分类数据:此类数据仅只有两类:例如是与否、成功与失败。
- 多分类数据:此类数据有多类:例如天气出太阳、下雨、阴天。
- 周期型数据:此类数据存在一个周期循环:例如周数月数。
那么问题来了,关于这三种系数到底适用于哪种数据场景呢?
二、皮尔逊系数使用场景
首先使用皮尔逊系数的情况包含以下三种特性,我们从scipy的函数pearsonr的相关说明就可以看出:
The Pearson correlation coefficient [1] measures the linear relationship between two datasets. Like other correlation coefficients, this one varies between -1 and +1 with 0 implying no correlation. Correlations of -1 or +1 imply an exact linear relationship. Positive correlations imply that as x increases, so does y. Negative correlations imply that as x increases, y decreases.
也就是说:
皮尔逊相关系数测量两个数据集之间的线性关系。与其他相关系数一样,该系数在-1和+1之间变化,0表示不相关。-1或+1的相关性意味着精确的线性关系。正相关意味着x增加,y也增加。负相关意味着随着x增加,y减少。
总结一下对于皮尔逊相关系数的使用场景,有三种必要的特性使用皮尔逊系数最佳:
- 连续数据
- 正态分布
- 线性关系
上述三个条件均满足才能使用pearson相关系数,否则就用spearman相关系数。定序数据之间也只用spearman相关系数,不能用pearson相关系数。
二、皮尔逊相关系数(Pearson correlation)
1.定义
两个变量之间的皮尔逊相关系数定义为两个变量之间的协方差和标准差的商:
上式定义了总体相关系数,常用希腊小写字母![]() 作为代表符号。估算样本的协方差和标准差,可得到皮尔逊相关系数,常用英文小写字母
作为代表符号。估算样本的协方差和标准差,可得到皮尔逊相关系数,常用英文小写字母![]() 代表:
代表:
![]() 亦可由
亦可由![]() 样本点的标准分数均值估计,得到与上式等价的表达式:
样本点的标准分数均值估计,得到与上式等价的表达式:
变量相关强度:
| 相关程度 | 极强相关 | 强相关 | 中等强度相关 | 弱相关 | 极弱相关或无相关 |
| 相关系数绝对值 | 1-0.8 | 0.8-0.6 | 0.6-0.4 |
0.4-0.2 | 0.2-0 |
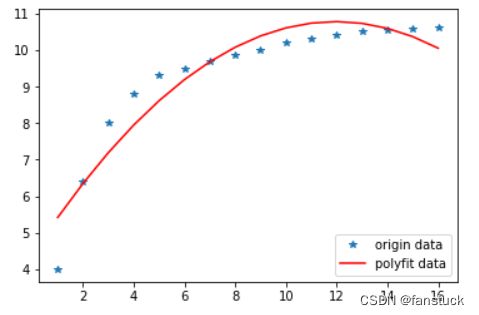
2.线性关系判定
3.正态检验
1.KS检验
假设检验的基本思想:
若对总体的某个假设是真实的,那么不利于或者不能支持这一假设的事件A在一次试验中是几乎不可能发生的。如果事件A真的发生了,则有理由怀疑这一假设的真实性,从而拒绝该假设。
实质分析:
假设检验实质上是对原假设是否正确进行检验,因此检验过程中要使原假设得到维护,使之不轻易被拒绝;否定原假设必须有充分的理由。同时,当原假设被接受时,也只能认为否定该假设的根据不充分,而不是认为它绝对正确。
借助假设检验的思想,利用K-S检验可以对数列的性质进行检验:
def normal_test(data):
u = data.mean()
std = data.std()
result = stats.kstest(data, 'norm', (u, std))
print(result)
normal_test()此时,pvalue > 0.05,不拒绝原假设。因此数据服从正态分布。
4.计算代码
若以上验证均成功则采取皮尔逊相关系数进行相关性分析,可以使用pandas的函数corr:
DataFrame.corr(method='pearson',
min_periods=1,
numeric_only=_NoDefault.no_default)
参数说明:
method:{‘pearson’, ‘kendall’, ‘spearman’} or callable。Method of correlation。
-
pearson : standard correlation coefficient,皮尔逊系数
-
kendall : Kendall Tau correlation coefficient,肯德尔系数
-
spearman :Spearman rank correlation,斯皮尔曼系数
min_periods:int, optional。每对列所需的最小样本数。目前仅适用于Pearson和Spearman相关性。
numeric_only:bool, default True。仅包含浮点、整型或布尔型数据。
rho =df_test.corr(method='pearson')
rho对生成的相关系数矩阵进行可视化操作(生成热力图):
plt.rcParams['font.family'] = ['SimHei']
plt.rcParams['axes.unicode_minus'] = False
sns.heatmap(rho, annot=True)
plt.title('Heat Map', fontsize=18)
点关注,防走丢,如有纰漏之处,请留言指教,非常感谢
以上就是本期全部内容。我是fanstuck ,有问题大家随时留言讨论 ,我们下期见
参阅
kstest 检验数据是否符合正态分布
数学建模:相关性分析学习——皮尔逊(pearson)相关系数与斯皮尔曼(spearman)相关系数
肯德尔(Kendall)相关系数概述及Python计算例