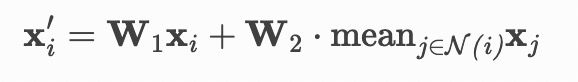【图神经网络】GraphSAGE 无监督训练源码剖析
概述
本教程主要介绍pytorch_geometric库examples下的graph_sage_unsup.py的源码剖析,主要的关键技术点,包括:
- 如何实现随机采样的?
- SAGEConv是如何训练的?
关键问题1,随机采样和采样方向的问题(有向图)
首先要理解的是,采样的过程和特征聚合的过程是相反的,采样的过程,比如,如下图所示,先采样A节点的一阶邻域节点,再根据一阶采样得到的节点进行二阶采样,是一个从左到右的采样过程,而在特征聚合消息传递的时候是先从二阶节点开始聚合,逐步收敛到目标节点A的过程(在关键问题2的训练阶段会谈到这个问题),是一个从右到左的过程。
同时,一个最重要的问题在于,如果图是有向图,那么采样函数是沿着节点A的出边采样,还是沿着入边采样呢?
以上图为例,如果采样是按照节点2的出边进行采样,那么N(2) = {3,5},上面说过消息传递是反向的,所以消息传递的方向是aggr(3,5) = 2,这显然与有向图的指向相反,通常情况下,有向图的指向应该代表了信息流动的方向,所以NeighborSampler.sample函数的采样并不是按照上述所说进行采样的,而是按照节点2的入边采样的,即N(2) = {0,1},这样在消息传递的时候,就是由aggr(0,1) = 2,正好跟有向图的方向一致!
代码验证如下:
import torch
import os.path as osp
import torch.nn as nn
import torch.nn.functional as F
from torch_cluster import random_walk
from sklearn.linear_model import LogisticRegression
import torch_geometric.transforms as T
from torch_geometric.nn import SAGEConv
from torch_geometric.datasets import Planetoid
from torch_geometric.data import NeighborSampler as RawNeighborSampler
from torch_geometric.data import Data
class NeighborSampler(RawNeighborSampler):
def sample(self, batch):
batch = torch.tensor(batch)
print("batch = ",batch)
return super(NeighborSampler, self).sample(batch)
edge_index = torch.tensor([[0,1,2,2,5,3],
[2,2,5,3,4,4]], dtype=torch.long)
x = torch.tensor([[-1,0,1], [0,-1,1], [1,0,-1],[1,0,-1],[1,0,-1],[-1,0,1],[-1,0,1]], dtype=torch.float)
data = Data(x=x, edge_index=edge_index)
train_loader = NeighborSampler(data.edge_index, sizes=[2], batch_size=1,
shuffle=True, num_nodes=data.num_nodes)
for batch_size,n_id,adjs in train_loader:
print("n_id:",n_id)
print("adjs:",adjs)
batch = tensor([2])
n_id: tensor([2, 1, 0])
adjs: EdgeIndex(edge_index=tensor([[1, 2],
[0, 0]]), e_id=tensor([1, 0]), size=(3, 1))
batch = tensor([4])
n_id: tensor([4, 5, 3])
adjs: EdgeIndex(edge_index=tensor([[1, 2],
[0, 0]]), e_id=tensor([4, 5]), size=(3, 1))
batch = tensor([5])
n_id: tensor([5, 2])
adjs: EdgeIndex(edge_index=tensor([[1],
[0]]), e_id=tensor([2]), size=(2, 1))
batch = tensor([1])
n_id: tensor([1])
adjs: EdgeIndex(edge_index=tensor([], size=(2, 0), dtype=torch.int64), e_id=tensor([], dtype=torch.int64), size=(1, 1))
batch = tensor([0])
n_id: tensor([0])
adjs: EdgeIndex(edge_index=tensor([], size=(2, 0), dtype=torch.int64), e_id=tensor([], dtype=torch.int64), size=(1, 1))
batch = tensor([6])
n_id: tensor([6])
adjs: EdgeIndex(edge_index=tensor([], size=(2, 0), dtype=torch.int64), e_id=tensor([], dtype=torch.int64), size=(1, 1))
batch = tensor([3])
n_id: tensor([3, 2])
adjs: EdgeIndex(edge_index=tensor([[1],
[0]]), e_id=tensor([3]), size=(2, 1))再者,graphsage_conv要想能够进行无监督训练,还需要构建正负样本,对于图上一批minibatch节点,其邻域节点就是作为其正样本,与该节点不连接的样本点作为负样本,为此源码中构建了一个随机采样函数NeighborSampler,看一下这个函数的实现:
from torch_geometric.data import NeighborSampler as RawNeighborSampler
class NeighborSampler(RawNeighborSampler):
def sample(self, batch): # sample 1
batch = torch.tensor(batch)
row, col, _ = self.adj_t.coo()
# For each node in `batch`, we sample a direct neighbor (as positive
# example) and a random node (as negative example):
pos_batch = random_walk(row, col, batch, walk_length=1,
coalesced=False)[:, 1]
neg_batch = torch.randint(0, self.adj_t.size(1), (batch.numel(), ),
dtype=torch.long)
batch = torch.cat([batch, pos_batch, neg_batch], dim=0)
return super(NeighborSampler, self).sample(batch) # sample 2第一阶段,假设batch样本量为256(即256为一批),pos_batch,通过random_walk,随机游走长度为1,进行采样得到,而neg_batch,是随机在图上进行采样获得,其shape均为256,最后的torch.cat([batch, pos_batch, neg_batch], dim=0)为256*3=768,作为源点;
第二阶段,调用sample函数进行采样,代码中,一阶和二阶中每个节点均从邻居中(如上面所示,会沿着节点入边进行采样)采样10个点,最后形成n_id包含了二阶采样的所有节点索引id,而adjs为列表,存储着一阶和二阶的子图对应的邻接矩阵。
其中,adjs列表元素由EdgeIndex(edge_index, e_id, size)构成:
- edge_index:每一阶的子图矩阵,source->target形式;
- e_id:子图边在全graph中的原始索引id;
- size:tuple形式,(K阶节点数,K-1阶节点数)
举个例子,例如我们的源点batch有768个节点,经过一阶采样后,一阶节点数为1826,二阶采样后节点数为2412,即采样过程中满足:768->1826->2412的变化,而在训练消息传递聚合的时候,是按照2412->1826->768的变化进行训练的。
def sample(self, batch):
if not isinstance(batch, Tensor):
batch = torch.tensor(batch)
batch_size: int = len(batch)
adjs = []
n_id = batch
for size in self.sizes:
adj_t, n_id = self.adj_t.sample_adj(n_id, size, replace=False)
e_id = adj_t.storage.value()
size = adj_t.sparse_sizes()[::-1]
if self.__val__ is not None:
adj_t.set_value_(self.__val__[e_id], layout='coo')
if self.is_sparse_tensor:
adjs.append(Adj(adj_t, e_id, size))
else:
row, col, _ = adj_t.coo()
edge_index = torch.stack([col, row], dim=0)
adjs.append(EdgeIndex(edge_index, e_id, size))
adjs = adjs[0] if len(adjs) == 1 else adjs[::-1]
out = (batch_size, n_id, adjs)
out = self.transform(*out) if self.transform is not None else out
return outtrain_loader = NeighborSampler(data.edge_index, sizes=[10, 10], batch_size=256,
shuffle=True, num_nodes=data.num_nodes)注意:需要明白这里面存在两种物理含义上的采样
sample 1,得到的pos_batch和neg_batch是为了用于计算loss所用,即:
![]()
sample 2,是图上的K阶采样,是用于特征聚合学习所用,即下图中的3-7行
关键问题2,sage_conv如何训练
正如上述所说,采样的时候是由向图方向反向实现K阶采样的,这样在训练的时候,特征聚合(消息传递)的过程是沿着图的方向进行的,即从第二层向源点进行消息传递。其中,n_id表示每个batch样本中二阶采样点的索引id(包含节点自身)。整个前向传播的out,分为三个部分,out,pos_out,neg_out,根据论文中的loss计算方式,用于反向传播:
def train():
model.train()
total_loss = 0
for batch_size, n_id, adjs in train_loader:
# `adjs` holds a list of `(edge_index, e_id, size)` tuples.
adjs = [adj.to(device) for adj in adjs]
optimizer.zero_grad()
out = model(x[n_id], adjs)
out, pos_out, neg_out = out.split(out.size(0) // 3, dim=0)
pos_loss = F.logsigmoid((out * pos_out).sum(-1)).mean()
neg_loss = F.logsigmoid(-(out * neg_out).sum(-1)).mean()
loss = -pos_loss - neg_loss
loss.backward()
optimizer.step()
total_loss += float(loss) * out.size(0)
return total_loss / data.num_nodes下面看一下model整个前向传播的计算。定义的SAGE模型如下,forward的传播过程如下:二阶->一阶->目标节点。
class SAGE(nn.Module):
def __init__(self, in_channels, hidden_channels, num_layers):
super(SAGE, self).__init__()
self.num_layers = num_layers
self.convs = nn.ModuleList()
for i in range(num_layers):
in_channels = in_channels if i == 0 else hidden_channels
self.convs.append(SAGEConv(in_channels, hidden_channels))
def forward(self, x, adjs):
for i, (edge_index, _, size) in enumerate(adjs):
x_target = x[:size[1]] # Target nodes are always placed first.
x = self.convs[i]((x, x_target), edge_index)
if i != self.num_layers - 1:
x = x.relu()
x = F.dropout(x, p=0.5, training=self.training)
return x
def full_forward(self, x, edge_index):
for i, conv in enumerate(self.convs):
x = conv(x, edge_index)
if i != self.num_layers - 1:
x = x.relu()
x = F.dropout(x, p=0.5, training=self.training)
return xtorch_geometric源码SAGEConv的定义,重点关注其forward函数,其计算过程是按照如下公式进行计算的:
根据上述公式,结合下面的源码可以看出,self.line_l和self.line_r分别对应这个公式中的
![]()
![]()
class SAGEConv(MessagePassing):
r"""The GraphSAGE operator from the `"Inductive Representation Learning on
Large Graphs" `_ paper
.. math::
\mathbf{x}^{\prime}_i = \mathbf{W}_1 \mathbf{x}_i + \mathbf{W}_2 \cdot
\mathrm{mean}_{j \in \mathcal{N(i)}} \mathbf{x}_j
Args:
in_channels (int or tuple): Size of each input sample. A tuple
corresponds to the sizes of source and target dimensionalities.
out_channels (int): Size of each output sample.
normalize (bool, optional): If set to :obj:`True`, output features
will be :math:`\ell_2`-normalized, *i.e.*,
:math:`\frac{\mathbf{x}^{\prime}_i}
{\| \mathbf{x}^{\prime}_i \|_2}`.
(default: :obj:`False`)
root_weight (bool, optional): If set to :obj:`False`, the layer will
not add transformed root node features to the output.
(default: :obj:`True`)
bias (bool, optional): If set to :obj:`False`, the layer will not learn
an additive bias. (default: :obj:`True`)
**kwargs (optional): Additional arguments of
:class:`torch_geometric.nn.conv.MessagePassing`.
"""
def __init__(self, in_channels: Union[int, Tuple[int, int]],
out_channels: int, normalize: bool = False,
root_weight: bool = True,
bias: bool = True, **kwargs): # yapf: disable
kwargs.setdefault('aggr', 'mean')
super(SAGEConv, self).__init__(**kwargs)
self.in_channels = in_channels
self.out_channels = out_channels
self.normalize = normalize
self.root_weight = root_weight
if isinstance(in_channels, int):
in_channels = (in_channels, in_channels)
self.lin_l = Linear(in_channels[0], out_channels, bias=bias)
if self.root_weight:
self.lin_r = Linear(in_channels[1], out_channels, bias=False)
self.reset_parameters()
def reset_parameters(self):
self.lin_l.reset_parameters()
if self.root_weight:
self.lin_r.reset_parameters()
def forward(self, x: Union[Tensor, OptPairTensor], edge_index: Adj,
size: Size = None) -> Tensor:
""""""
if isinstance(x, Tensor):
x: OptPairTensor = (x, x)
# propagate_type: (x: OptPairTensor)
out = self.propagate(edge_index, x=x, size=size)
out = self.lin_l(out)
x_r = x[1]
if self.root_weight and x_r is not None:
out += self.lin_r(x_r)
if self.normalize:
out = F.normalize(out, p=2., dim=-1)
return out 参考链接
论文链接:https://arxiv.org/abs/1706.02216
github链接:https://github.com/rusty1s/pytorch_geometric/blob/master/examples/graph_sage_unsup.py
https://github.com/rusty1s/pytorch_geometric/issues/2816
官方文档:https://pytorch-geometric.readthedocs.io/en/latest/modules/nn.html?highlight=SAGEConv#torch_geometric.nn.conv.SAGEConv.forward
知乎链接:https://www.zhihu.com/people/zhang-kang-5-20/posts