【机器学习】关联规则挖掘算法 + 三大案例实战 + Apriori算法 + Python代码实现

---

一、关联规则概述

1.1 关联规则引入

下面用一个故事来引出关联规则：

1.2 关联规则相关概念介绍

1.2.1 样本、事务、项集、规则

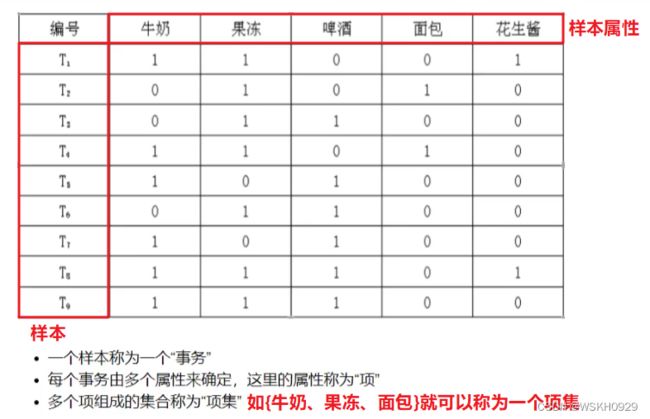
关联规则中的数据集结构一般如下所示：

关于项集（多个项组成的集合）：

• { 牛奶 } 是 1-项集
• { 牛奶，果冻 } 是 2-项集；
• { 啤酒，面包，牛奶 } 是 3-项集

X==>Y含义（规则）：

• X和Y是项集
• X称为规则前项
• Y称为规则后项

事务：即样本，一个样本称为一个事务。事务仅包含其涉及到的项目，而不包含项目的具体信息

• 在超级市场的关联规则挖掘问题中事务是顾客一次购物所购买的商品，但事务中并不包括这些商品的具体信息，如商品的数量、价格等

1.2.2 支持度、置信度

支持度(support)：一个项集或者规则在所有事务中出现的频率，$\sigma (\mathrm{X})$：表示项集X的支持度计数

• 项集X的支持度：$s(X)=\sigma (\mathrm{X})÷N$
• 规则X==>Y表示物品集X对物品集Y的支持度，也就是物品集X和物品集Y同时出现的概率
• 假设某天共有100个顾客到商场买东西，其中30个顾客同时购买了啤酒和尿布，那么上述的关联规则的支持度就是30%

置信度(confidence)：确定Y在包含X的事务中出现的频繁程度。$c(X⟶Y)=\sigma (X\cup Y)÷\sigma (X)$

• 条件概率公式：$P(Y|X)=P(XY)÷P(X)$
• 置信度反映了关联规则的可信度，即购买了项目集X中的商品的顾客同时也购买了Y中商品的概率
• 假设购买薯片的顾客中有50%也购买了可乐，则置信度为50%

下面举一个例子，来更深层次的理解支持度和置信度：

计算 A==>C 的支持度和置信度：

• 支持度：即同时购买了商品A和C的顾客的比率 = $2÷4=50\%$
• 置信度：即在购买了商品A的顾客中，购买了商品C的比率 = $2÷3=66.7\%$

计算 C==>A 的支持度和置信度：

• 支持度：即同时购买了商品C和A的顾客的比率（其实和A==>C的支持度是一样的） = $2÷4=50\%$
• 置信度：即在购买了商品C的顾客中，购买了商品A的比率 = $2÷2=100\%$

我们一般可以用 X==>Y（支持度，置信度）的格式表示规则的支持度和置信度，具体如下所示：

• A==>C（50%，66.7%）
• C==>A（50%，100%）

一般地，我们会定义最小支持度（minsupport）和最小置信度（minconfidence），若规则X==>Y的支持度分别大于等于我们定义的最小支持度和最小置信度，则称关联规则X==>Y为强关联规则，否则称为弱关联规则。我们通常会把注意力放在强关联规则上。

1.2.3 提升度

提升度（lift）：物品集A的出现对物品集B的出现概率发生了多大的变化

• $lift(A==>B)=confidence(A==>B)÷support(B)=P(B|A)÷P(B)$
• 假设现在有1000个顾客，其中500人买了茶叶，买茶叶的500人中有450人还买了咖啡。那么可以计算得 $confidence(茶叶==>咖啡)=450÷500=90\%$，由此，可能会认为喜欢喝茶的人往往喜欢喝咖啡。但是，如果另外没有购买茶叶的500人中也有450人买了咖啡，同样可以算出置信度90%，得到的结论是不爱喝茶的人往往喜欢喝咖啡。这与前面的结论矛盾了，由此看来，实际上顾客喜不喜欢喝咖啡和他喜不喜欢喝茶几乎没有关系，两者是相互独立的。此时，我们就有提升度这一指标来描述这一现象。
  在这个例子中，$lift(茶叶==>咖啡)=confidence(茶叶==>咖啡)÷support(咖啡)=90\%÷[(450+450)÷1000]=1$
• 由此可见，提升度弥补了置信度的这一缺憾，如果提升都等于1，那么X与Y独立，X对Y的出现的可能性没有提升作用。提升度越大（lift > 1），则表明X对Y的提升程度越大，也表明X与Y的关联性越强。

1.2.4 所有指标的公式

---

二、Python实战关联规则

2.1 使用 mlxtend 工具包得出频繁项集与规则

2.1.1 安装 mlxtend 工具包

pip install mlxtend

2.1.2 引入相关库

import pandas as pd
# 设置pandas输出表格的属性
pd.options.display.max_colwidth=100
pd.options.display.width=500
from mlxtend.frequent_patterns import apriori, association_rules

2.1.3 自定义一份数据集

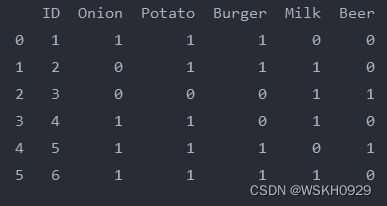
# 自定义一份数据集
data = {
    'ID': [1, 2, 3, 4, 5, 6],
    'Onion': [1, 0, 0, 1, 1, 1],
    'Potato': [1, 1, 0, 1, 1, 1],
    'Burger': [1, 1, 0, 0, 1, 1],
    'Milk': [0, 1, 1, 1, 0, 1],
    'Beer': [0, 0, 1, 0, 1, 0],
}
df = pd.DataFrame(data)
print(df)

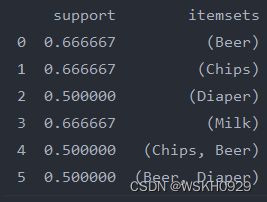
2.1.4 得到频繁项集

# 利用mlxtend提供的apriori算法函数得到频繁项集，其中设置最小支持度为50%
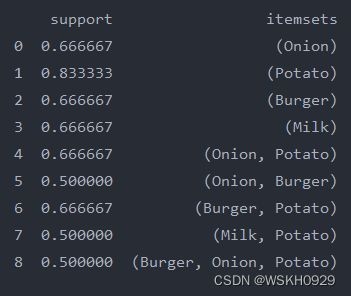
frequent_item_sets = apriori(df[['Onion', 'Potato', 'Burger', 'Milk', 'Beer']], min_support=0.50, use_colnames=True)
print(frequent_item_sets)

2.1.5 计算规则

# 计算规则，并设置提升度阈值为 1 （返回的是各个指标的数值，可以按照按兴趣的指标排序观察，但具体解释还得参考实际数据的含义）
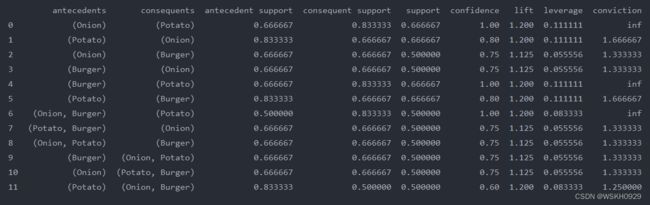
rules = association_rules(frequent_item_sets, metric='lift', min_threshold=1)
print(rules)

2.1.6 挑选有用的规则进行分析

print(rules[(rules['lift'] > 1.125) & (rules['confidence'] > 0.8)])

通过一些自定义条件，筛选出自己感兴趣的结果。如上，我们可以分析得：

• （洋葱和马铃薯）（汉堡和马铃薯）可以搭配着来卖
• 如果洋葱和汉堡都在顾客的购物篮中，顾客购买马铃薯得可能性也较高，如果他篮子里没有，则可以推荐一下

2.2 数据集制作

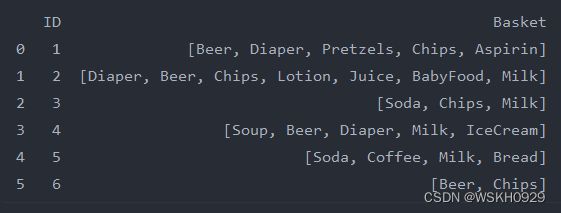
实际场景中，我们拿到的数据往往如下图所示：

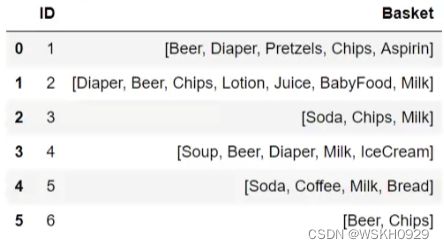
也就是说，我们的初始输出往往是每个顾客购买了哪些商品，都是字符串类型的，而并非像我们上一节用到的那种标准格式的。这一节就讲讲怎么讲上面的原始数据转化为我们需要的格式。

导入相关库

import pandas as pd

# 设置pandas输出表格的属性
pd.options.display.max_colwidth = 100
pd.options.display.width = 500
from mlxtend.frequent_patterns import apriori, association_rules

构建原始数据集

# 原始数据集
data = {
    'ID': [1, 2, 3, 4, 5, 6],
    'Basket': [
        ['Beer', 'Diaper', 'Pretzels', 'Chips', 'Aspirin'],
        ['Diaper', 'Beer', 'Chips', 'Lotion', 'Juice', 'BabyFood', 'Milk'],
        ['Soda', 'Chips', 'Milk'],
        ['Soup', 'Beer', 'Diaper', 'Milk', 'IceCream'],
        ['Soda', 'Coffee', 'Milk', 'Bread'],
        ['Beer', 'Chips']
    ]
}
data = pd.DataFrame(data)
print(data)

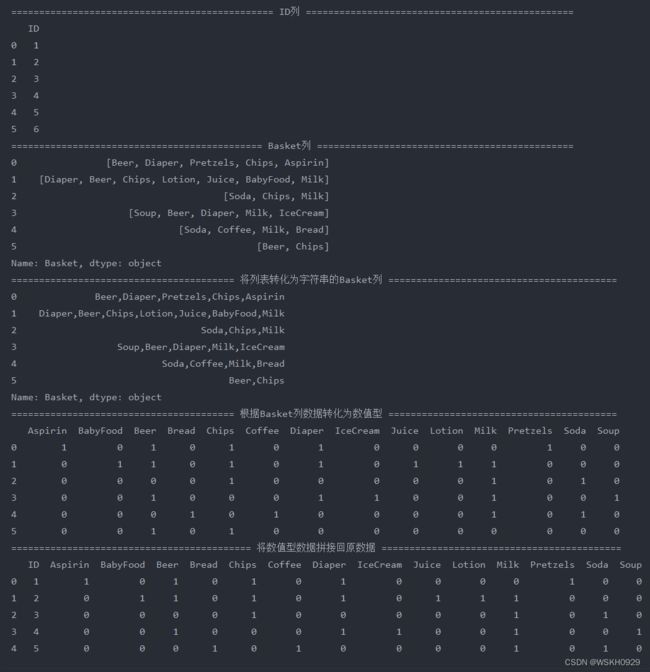
处理成标准格式

# 将 Basket 列取出来单独处理，然后再将处理好的数据拼接回去
print(" ID列 ".center(100, '='))
data_id = data.drop('Basket', 1)
print(data_id)

print(" Basket列 ".center(100, '='))
basket = data.Basket
print(basket)

print(" 将列表转化为字符串的Basket列 ".center(100, '='))
basket = data.Basket.str.join(',')
print(basket)

print(" 根据Basket列数据转化为数值型 ".center(100, '='))
basket = basket.str.get_dummies(',')
print(basket)

print(" 将数值型数据拼接回原数据 ".center(100, '='))
data = data_id.join(basket)
print(data)

用标准数据继续关联规则分析的步骤

# 用标准数据继续关联规则分析的步骤
# 利用mlxtend提供的apriori算法函数得到频繁项集，其中设置最小支持度为50%
frequent_item_sets = apriori(data[['Aspirin', 'BabyFood', 'Beer', 'Bread', 'Chips', 'Coffee', 'Diaper', 'IceCream',
                                   'Juice', 'Lotion', 'Milk', 'Pretzels', 'Soda', 'Soup']], min_support=0.50,
                             use_colnames=True)
print(frequent_item_sets)

计算规则

# 计算规则，并设置提升度阈值为 1 （返回的是各个指标的数值，可以按照按兴趣的指标排序观察，但具体解释还得参考实际数据的含义）
rules = association_rules(frequent_item_sets, metric='lift', min_threshold=1)
print(rules)

2.3 电影数据集关联分析

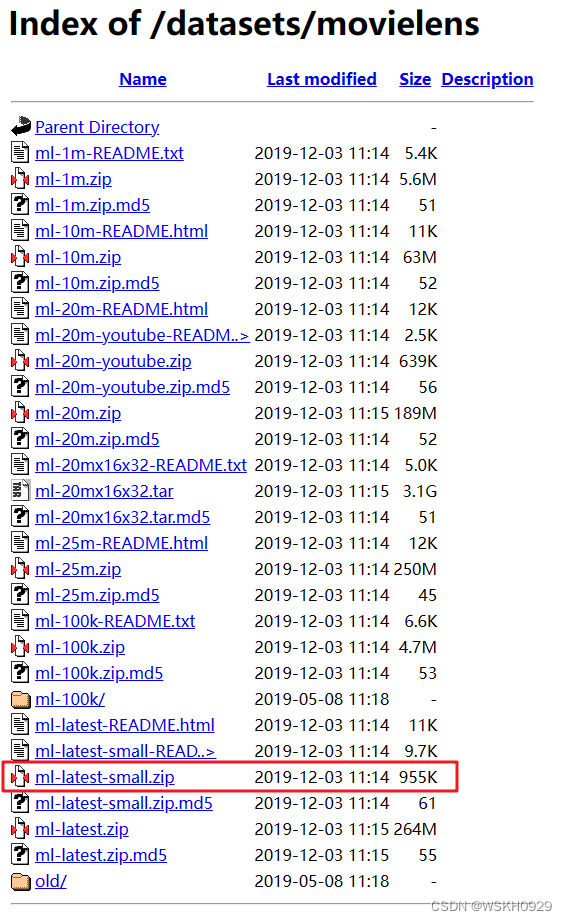
2.3.1 数据集获取

数据集链接

2.3.2 引入相关库

import pandas as pd

# 设置pandas输出表格的属性
pd.options.display.max_colwidth = 100
pd.options.display.width = 500
from mlxtend.frequent_patterns import apriori, association_rules

2.3.3 读取数据集

# 读取原始数据
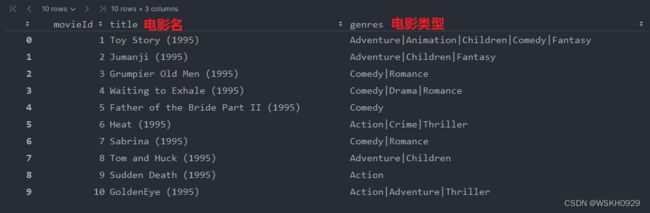
movies = pd.read_csv(
    r'E:\Software\JetBrainsIDEA\PythonIDEA\Projects\CXSJS\Python\机器学习\唐宇迪机器学习\关联规则\data\movies\movies.csv')
movies.head(10)

2.3.4 标准化数据集

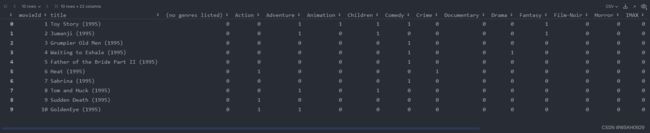
# 第一步，当然是将原始数据转化为标准格式啦
movies_standard = movies.drop('genres', 1).join(movies.genres.str.get_dummies())
movies_standard.head(10)
# 一共包含 9742 部电影，一共有20种不同的电影类型（有2列是ID和电影名）
print(movies_standard.shape)  # (9742, 22)

2.3.5 获取频繁项集

# 利用mlxtend提供的apriori算法函数得到频繁项集，其中设置最小支持度为0.05
movies_standard.set_index(['movieId', 'title'], inplace=True)
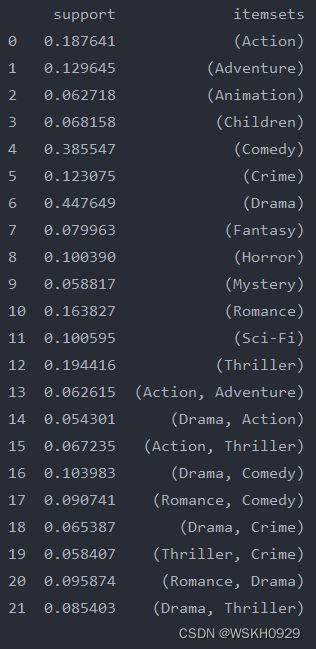
frequent_item_sets = apriori(movies_standard, min_support=0.05, use_colnames=True)
print(frequent_item_sets)

2.3.6 计算规则

# 计算规则，并设置提升度阈值为 1.25 （返回的是各个指标的数值，可以按照按兴趣的指标排序观察，但具体解释还得参考实际数据的含义）
rules = association_rules(frequent_item_sets, metric='lift', min_threshold=1.25)
print(rules)

2.3.7 结果分析

# 对lift降序排序，查看lift较大的是哪些规则
rules_sort = rules.sort_values(by=['lift'], ascending=False)
print(rules_sort)

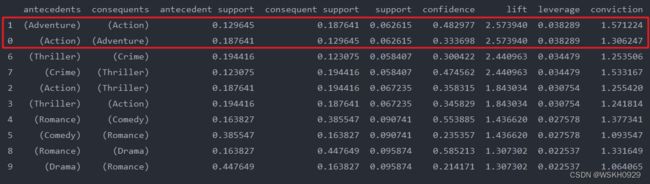
由上图可知，Adventure（冒险） 和 Action（动作片） 两个类型是最相关的，这和常识相符。

---

三、Apriori 算法

3.1 算法介绍

假设现在有 4 个项（0、1、2、3），那么需要找出频繁项集的话就需要遍历所有可能的项集，一共15个（如下图所示）

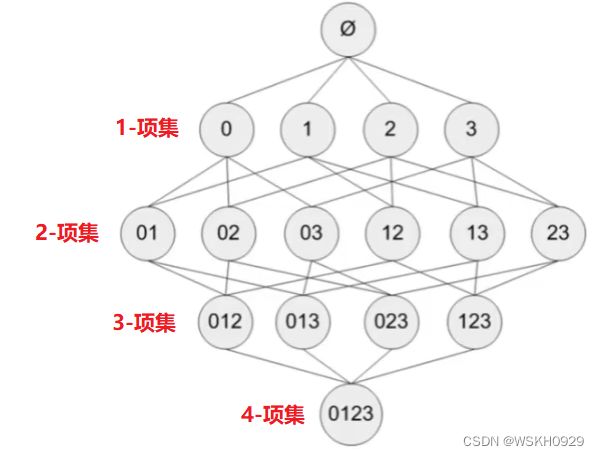
假设现在有 $n$ 个项，那么所有可能的项集就有 $2^n-1$ 个，显然，当 $n$ 较大时，采用暴力遍历的方法寻找频繁项集是不可行的。所以就有人提出了 Apriori 算法来减少遍历的次数。

首先，我们要知道一个定理，如果一个项集是非频繁项集，那么它的超集一定也是非频繁的。这个定理很容易理解，比如项集{2,3}是非频繁的，那么它的一个超集{1,2,3}肯定也是非频繁的，为什么呢？因为{1,2,3}出现的概率肯定小于等于{2,3}出现的概率，如果{2,3}都是非频繁的，那么出现概率更小的{1,2,3}当然也是非频繁的啦！

Apriori 算法的思想就是，在遍历的时候采用上述定理进行剪枝，从而减少遍历次数。

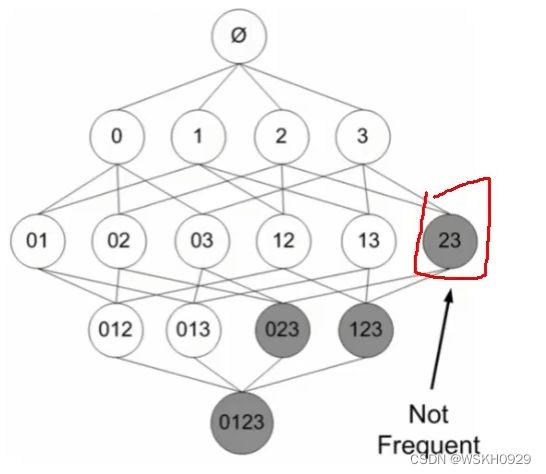
如下图所示，采用 Apriori 算法，假设项集{2,3}是非频繁的，那么项集{023}、{123}和{0123}肯定都是非频繁的。所以可以不用遍历它们。

3.2 Python代码实现

案例：求下图所示数据集的频繁项集并计算规则

代码

import math
import time


def get_item_set(data):
    '''
    获取项的字典
    :param data: 数据集
    :return: 项的字典
    '''
    item_set = set()
    for d in data:
        item_set = item_set | set(d)
    return item_set


def apriori(item_set, data, min_support=0.50):
    '''
    获取频繁项集
    :param item_set: 项的字典
    :param data: 数据集
    :param min_support: 最小支持度，默认为0.50
    :return: None
    '''
    # 初始化存储非频繁项集的列表
    infrequent_list = []
    # 初始化存储频繁项集的列表
    frequent_list = []
    # 初始化存储频繁项集的支持度的列表
    frequent_support_list = []
    # 遍历获取 n-项集
    for n in range(1, len(item_set) + 1):
        c = []
        supports = []
        if len(frequent_list) == 0:
            # 计算 1-项集
            for item in item_set:
                items = {item}
                support = calc_support(data, items)
                # 如果支持度大于等于最小支持度就为频繁项集
                if support >= min_support:
                    c.append(items)
                    supports.append(support)
                else:
                    infrequent_list.append(items)
        else:
            # 计算 n-项集，n > 1
            for last_items in frequent_list[-1]:
                for item in item_set:
                    if item > list(last_items)[-1]:
                        items = last_items.copy()
                        items.add(item)
                        # 如果items的子集没有非频繁项集才计算支持度
                        if is_infrequent(infrequent_list, items) is False:
                            support = calc_support(data, items)
                            # 如果支持度大于等于最小支持度就为频繁项集
                            if support >= min_support:
                                c.append(items)
                                supports.append(support)
                            else:
                                infrequent_list.append(items)
        frequent_list.append(c)
        frequent_support_list.append(supports)
        print(f"{n}-项集: {c} , 支持度分别为: {supports}")
    return infrequent_list, frequent_list, frequent_support_list


def is_infrequent(infrequent_list, items):
    '''
    判断是否属于非频繁项集的超集
    :param infrequent_list: 非频繁项集列表
    :param items: 项集
    :return: 是否属于非频繁项集的超集
    '''
    for infrequent in infrequent_list:
        if infrequent.issubset(items):
            return True
    return False


def calc_support(data, items):
    '''
    计算 support
    :param data: 数据集
    :param items: 项集
    :return: 计算好的支持度
    '''
    cnt = 0
    for d in data:
        if items.issubset(d):
            cnt += 1
    return cnt / len(data)


def generate_rules(frequent_list, data, min_confidence=0.60):
    '''
    根据频繁项集和最小置信度生成规则
    :param frequent_list: 存储频繁项集的列表
    :param data: 数据集
    :param min_confidence: 最小置信度
    :return: 规则
    '''
    rule_key_set = set()
    rules = []
    for frequent in frequent_list:
        for items in frequent:
            if len(items) > 1:
                for n in range(1, math.ceil(len(items) / 2) + 1):
                    front_set_list = get_all_combine(list(items), n)
                    for front_set in front_set_list:
                        back_set = items - front_set
                        confidence = calc_confidence(front_set, items, data)
                        if confidence >= min_confidence:
                            rule = (front_set, back_set, confidence)
                            key = f'{front_set} ==> {back_set} , confidence: {confidence}'
                            if key not in rule_key_set:
                                rule_key_set.add(key)
                                rules.append(rule)
                                print(f"规则{len(rules)}: {key}")
    return rules


def get_all_combine(data_set, length):
    '''
    在指定数据集种获取指定长度的所有组合
    :param data_set: 数据集
    :param length: 指定的长度
    :return: 所有符合约束的组合
    '''

    def dfs(cur_index, cur_arr):
        if cur_index < len(data_set):
            cur_arr.append(data_set[cur_index])
            if len(cur_arr) == length:
                combine_list.append(set(cur_arr))
            else:
                for index in range(cur_index + 1, len(data_set)):
                    dfs(index, cur_arr.copy())

    combine_list = []

    for start_index in range(len(data_set)):
        dfs(start_index, [])

    return combine_list


def calc_confidence(front_set, total_set, data):
    '''
    计算规则 X==>Y 的置信度
    :param front_set: X
    :param total_set: X ∪ Y
    :param data: 数据集
    :return: 返回规则 X==>Y 的置信度
    '''
    front_cnt = 0
    total_cnt = 0
    for d in data:
        if front_set.issubset(d):
            front_cnt += 1
        if total_set.issubset(d):
            total_cnt += 1
    return total_cnt / front_cnt


if __name__ == '__main__':
    # 记录开始时间
    s = time.time()

    # 数据集
    data = [
        [1, 3, 4],
        [2, 3, 5],
        [1, 2, 3, 5],
        [2, 5]
    ]

    # 获取项的字典
    item_set = get_item_set(data)
    print("项的字典:", item_set)

    # 根据 Apriori算法 获取 n-频繁项集
    infrequent_list, frequent_list, frequent_support_list = apriori(item_set, data, min_support=0.50)

    # 生成规则
    rule_set = generate_rules(frequent_list, data, min_confidence=0.60)

    # 输出总用时
    print("总用时:", (time.time() - s), "s")

运行输出

项的字典: {1, 2, 3, 4, 5}
1-项集: [{1}, {2}, {3}, {5}] , 支持度分别为: [0.5, 0.75, 0.75, 0.75]
2-项集: [{1, 3}, {2, 3}, {2, 5}, {3, 5}] , 支持度分别为: [0.5, 0.5, 0.75, 0.5]
3-项集: [{2, 3, 5}] , 支持度分别为: [0.5]
4-项集: [] , 支持度分别为: []
5-项集: [] , 支持度分别为: []
规则1: {1} ==> {3} , confidence: 1.0
规则2: {3} ==> {1} , confidence: 0.6666666666666666
规则3: {2} ==> {3} , confidence: 0.6666666666666666
规则4: {3} ==> {2} , confidence: 0.6666666666666666
规则5: {2} ==> {5} , confidence: 1.0
规则6: {5} ==> {2} , confidence: 1.0
规则7: {3} ==> {5} , confidence: 0.6666666666666666
规则8: {5} ==> {3} , confidence: 0.6666666666666666
规则9: {2} ==> {3, 5} , confidence: 0.6666666666666666
规则10: {3} ==> {2, 5} , confidence: 0.6666666666666666
规则11: {5} ==> {2, 3} , confidence: 0.6666666666666666
规则12: {2, 3} ==> {5} , confidence: 1.0
规则13: {2, 5} ==> {3} , confidence: 0.6666666666666666
规则14: {3, 5} ==> {2} , confidence: 1.0
总用时: 0.0 s