Automatic Online Calibration of Cameras and Lasers 论文翻译
目录
- 题目
- Abstract
- I. INTRODUCTION
- II. SENSOR PROCESSING
-
- A. Image processing
- B. Laser processing
- III. MISCALIBRATION DETECTION
- IV. AUTOMATIC CALIBRATION TRACKING
- V. EXPERIMENTAL RESULTS
- VI. CONCLUSION
题目
Automatic Online Calibration of Cameras and Lasers
下载地址: http://www.roboticsproceedings.org/rss09/p29.pdf
Abstract
The combined use of 3D scanning lasers with 2D cameras has become increasingly popular in mobile robotics, as the sparse depth measurements of the former augment the dense color information of the latter. Sensor fusion requires precise 6- DOF transforms between the sensors, but hand-measuring these values is tedious and inaccurate. In addition, autonomous robots can be rendered inoperable if their sensors’ calibrations change over time. Yet previously published camera-laser calibration algorithms are offline only, requiring significant amounts of data and/or specific calibration targets; they are thus unable to correct calibration errors that occur during live operation.
3D扫描激光与2D相机的结合使用在移动机器人中变得越来越流行,因为前者的稀疏深度测量增加了后者的稠密颜色信息。传感器融合需要在传感器之间进行精确的6自由度变换,但手动测量这些值既繁琐又不准确。此外,如果传感器的校准值随时间变化,自主机器人可能无法运行。然而,先前发布的相机激光校准算法仅可以离线执行,需要大量数据和/或特定校准目标;因此它们不能校正在带电操作期间发生的校准误差。
In this paper, we introduce two new real-time techniques that enable camera-laser calibration online, automatically, and in arbitrary environments. The first is a probabilistic monitoring algorithm that can detect a sudden miscalibration in a fraction of a second. The second is a continuous calibration optimizer that adjusts transform offsets in real time, tracking gradual sensor drift as it occurs.
在本文中,我们介绍了两种新的实时技术,可以在线、自动和在任意环境中进行相机激光校准。第一种是一种概率监控算法,可以在几分之一秒内检测到突然的校准错误。第二种是连续校准优化器,它实时调整变换偏移,在传感器漂移发生时跟踪传感器的逐渐漂移。
Although the calibration objective function is not globally convex and cannot be optimized in real time, in practice it is always locally convex around the global optimum, and almost everywhere else. Thus, the local shape of the objective function at the current parameters can be used to determine whether the sensors are calibrated, and allows the parameters to be adjusted gradually so as to maintain the global optimum.
尽管校准目标函数不是全局凸的,并且不能实时优化,但实际上它总是围绕全局最优值局部凸的,几乎在其他任何地方都是如此。因此,目标函数在当前参数下的局部形状可用于确定传感器是否被校准,并允许逐渐调整参数以保持全局最优。
需要保证标定前的转换矩阵有70%~80%的准度
In several online experiments on thousands of frames in real markerless scenes, our method automatically detects miscalibrations within one second of the error exceeding .25 deg or 10cm, with an accuracy of 100%. In addition, rotational sensor drift can be tracked in real-time with a mean error of just .10 deg. Together, these techniques allow significantly greater flexibility and adaptability of robots in unknown and potentially harsh environments.
在对真实无标记场景中的数千帧进行的几次在线实验中,我们的方法在误差超过0.25度或10厘米的一秒内自动检测错误,准确率为100%。此外,旋转传感器漂移可实时跟踪,平均误差仅为0.10度。总之,这些技术使机器人在未知和潜在恶劣环境中具有更大的灵活性和适应性。
I. INTRODUCTION
II. SENSOR PROCESSING
The goal of our algorithm is to take a series of corresponding camera images and laser scans, captured over time in an arbitrary environment, and to automatically determine the true 6-dimensional transform between the two sensors. Specifically, the six values are the x, y, and z translations, and the roll, pitch, and yaw Euler angle rotations between the two sensors. These six parameters uniquely determine the calibration. Whereas in previous work [20] we assumed the calibration to be rigid during the entire time spanned by the data, here we relax that constraint, and instead approximate the calibration as rigid only over much shorter windows of time.
我们算法的目标是在任意环境中拍摄一系列相应的相机图像和激光扫描,并自动确定两个传感器之间的真实6维变换。具体来说,这六个值是x、y和z平移,以及两个传感器之间的横摇、俯仰和偏航欧拉角旋转。这六个参数唯一地决定了校准。尽管在之前的工作[20]中,我们假设校准在数据所跨越的整个时间内是刚性的,但在这里我们放松了这一约束,而是仅在更短的时间窗口内将校准近似为刚性。
An underlying assumption, which is used in [16], and which [20] showed to be very robust, is that, everything else being equal, depth discontinuities in laser data should project onto edges in images more often when using accurate calibrations than when not. Across a series of frames, even a weak signal should overwhelm considerable noise.
[16]中使用了一个基本假设,[20]证明该假设非常稳健,即在其他条件相同的情况下,使用精确校准时,激光数据中的深度不连续性应比不使用时更频繁地投射到图像边缘。在一系列帧中,即使是微弱的信号也会压倒相当大的噪声
We assume that the camera images are already calibrated for their intrinsic parameters (e.g. geometric distortion), either with manufacturer-supplied values or through another calibration procedure, e.g. [13]. The laser data is assumed to cover a field of view at least partially overlapping the camera, and to come from multiple rotating beams, or a single beam on a pan/tilt mount.
我们假设摄像机图像已经使用制造商提供的值或通过其他校准程序(例如[13])针对其固有参数(例如几何失真)进行了校准。假设激光数据覆盖至少部分与相机重叠的视场,并且来自多个旋转光束,或平移/倾斜安装上的单个光束。
The camera and laser data may either be captured simultaneously, or if they are not, then any time offsets between the two sensors should be accounted for. Temporal correction is easily achieved by projecting each laser point from the laser’s origin at the time of detection. If a laser rotates while the robot is moving, an IMU (or other device) can be used to track the laser’s position over time, which allows laser points to be projected into the camera image based on the laser’s position at time the image was captured. In such a case, it is helpful to first calibrate the location of laser itself [9, 11, 8, 21]; we use the procedure described in [8], which also works automatically and in arbitrary scenes.
摄像机和激光数据可以同时被捕获,或者如果它们不被捕获,则应考虑两个传感器之间的任何时间偏移。通过在检测时从激光原点投影每个激光点,可以容易地实现时间校正。如果机器人在移动时激光旋转,则可以使用IMU(或其他设备)来跟踪激光随时间的位置,这允许基于图像捕获时激光的位置将激光点投影到相机图像中。在这种情况下,首先校准激光器本身的位置是有帮助的[9,11,8,21];我们使用[8]中描述的过程,该过程也可以在任意场景中自动工作。
A. Image processing
Assume we are given a series of camera images I 1 : n I^{1:n} I1:n and point clouds P 1 : n P^ {1:n} P1:n from n frames. Since the goal is to align laser depth discontinuities with image edges, we filter each camera frame I i I^i Ii to give a metric of the “edginess” of each pixel. We use a two-step process. First, each image is converted to grayscale, and each pixel is set to the largest absolute value of the difference between it and any of its 8 neighbors. We call this edge image E; an example is shown in Fig.3.
假设我们从n帧获得一系列 相机图像 I 1 : n I^{1:n} I1:n和点云 P 1 : n P^{1:n} P1:n。由于目标是将激光深度不连续性与图像边缘对齐,因此我们对每个相机帧 I I I^I II进行过滤,以给出每个像素的“边缘”度量。我们采用两步流程。首先,将每个图像转换为灰度,并将每个像素设置为其与8个相邻像素之间的差值的最大绝对值。我们将此边缘图像称为E;示例如图3所示。

Next, we apply an inverse distance transform to each edge image E 1 : n E^{1:n} E1:n, in order to reward laser points which hit pixels near edges; effectively, this smooths out the objective function and thus helps to avoid local optima in the search procedure. We use the L1 distance for ease of computation; in doing so, we can apply the transform in time linear in the number of pixels. Effectively, each edge has an exponential spilloff into its neighbors. Each pixel D i , j D_{i,j} Di,j is computed as follows:
接下来,我们对每个边缘图像 E 1 : n E^{1:n} E1:n应用逆距离变换,以奖励击中边缘附近像素的激光点;这有效地平滑了目标函数,从而有助于避免搜索过程中的局部最优。为了便于计算,我们使用L1距离;在这样做的时候,我们可以在像素数量上应用时间线性变换。实际上,每条边都有一个指数扩散到它的邻居。每个像素 D i , j D_{i,j} Di,j的计算如下:

逆矩阵变换可以理解为高斯模糊化,目的是为了处理激光点和图像点之间的一致性联系。
where i, j and x, y each correspond to row and column indices for pixels in the image. We use α = 1 / 3 α = 1/3 α=1/3 and γ = 0.98 γ = 0.98 γ=0.98, as in[20]. Examples of images after the inverse distance transformis applied are shown in Fig.2 (bottom), and a before/after comparison is shown in Fig.3.
其中i、j和x、y分别对应于图像中像素的行和列索引。我们使用 α = 1 / 3 α=1/3 α=1/3和 γ = 0.98 γ=0.98 γ=0.98,如[20]所示。应用反距离变换后的图像示例如图2(底部)所示,前后对比如图3所示。
B. Laser processing
For laser returns, we consider each beam independently, and look for points that are closer than at least one of their two neighbors; due to parallax and occlusion, points which are farther than their neighbors are less likely to coincide with an image edge. Specifically, we use each point cloud P i P^i Pi to compute a new point cloud X i X^i Xi , where each point p in X i X^i Xi is assigned a value as follows:
对于激光返回信息,我们独立地考虑每个光束,并寻找两个相邻光束中至少一个更近的点;由于视差和遮挡,比相邻点更远的点不太可能与图像边缘重合。具体来说,我们使用每个点云 P i P^i Pi来计算新的点云 X i X^i Xi,其中 X i X^i Xi中的每个点P都被分配了一个值,如下所示:
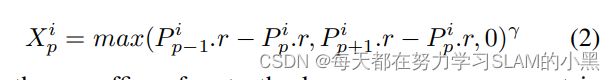
P p − 1 i . r − P p i . r P^i_{p-1}.r-P^i_p.r Pp−1i.r−Ppi.r : 表示当前激光光束的距离长度和相邻前一束的长度的差值
x p I = m a x ( P p − 1 i . r − P p i . r , P p + 1 i . r − P p i . r , 0 ) γ x^I_p = max(P^i_{p-1}.r-P^i_p.r,P^i_{p+1}.r-P^i_p.r,0)^\gamma xpI=max(Pp−1i.r−Ppi.r,Pp+1i.r−Ppi.r,0)γ:表示选取激光点中当前激光光束的距离长度比前后相邻激光束的距离长度都要长的激光点,那么这个激光点就是激光角点。
Here, the .r suffix refers to the laser range measurement in meters corresponding to that point. We use γ = . 5 γ = .5 γ=.5, and for efficiency, we filter out all points with a depth discontinuity of less than 30cm. The laser points in Fig.2 (Top) correspond to the points selected in X.
这里,.r后缀是指与该点相对应的激光测距(单位:米)。我们使用 γ = . 5 γ=.5 γ=.5,为了效率,我们过滤掉深度不连续性小于30cm的所有点。图2(顶部)中的激光点对应于X中选择的点。

图2.两个帧,显示了RGB相机图像,其中激光点对应于以绿色覆盖的深度不连续性(顶部)和应用了反距离变换的处理相机图像(底部)。在足够数量的帧中,精确的相机激光校准将使绿色点与红色边缘重合,而不是不准确的校准。
III. MISCALIBRATION DETECTION
Given a calibration C, we can project all laser points in X i X^i Xi onto the image D i D^i Di using basic geometry; we consider only those points which actually fall in the image. Unlike the offline case in which C would be scored across all n frames in the dataset, here we compute the objective function J C J_C JC over just the last w frames, where w is our window size:
给定校准C,我们可以使用基本几何将 X i X^i Xi中的所有激光点投影到图像 D i D^i Di上;我们只考虑那些实际落在图像中的点。与离线情况不同,在离线情况下,C将是数据集中的所有n帧上得分,这里我们仅在最后w帧上计算目标函数 J C J_C JC,其中w是我们的窗口大小:
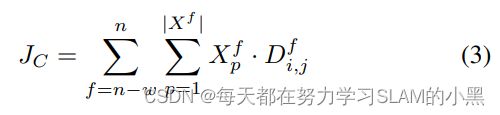
目标函数的意思是将前面计算出的激光点角点标量信息值和图像处理信息相乘再求和,得到一个概率检测标量 J c J_c Jc
如果离线标定准确,那么角点激光点通过离线标定得到的对应图像的像素点应该都是像素亮点,就是像素值为255的点,如果所有的激光点都是像素亮点,那么该算法得到的标量值 J c J_c Jc应该是最大的。通过目标函数 J c J_c Jc就可以判断该函数的标定是和否准确,是否发生偏移。
where f iterates over all frames, p iterates over all 3D points in X f X^f Xf , and (i, j) refers to the coordinates in image space onto which point p projects. Put simply, this function sums up the depth discontinuities at each laser return in X times the “edginess” of D for some calibration C.
其中f在所有帧上迭代,p在 X f X^f Xf中的所有3D点上迭代,并且(i,j)指的是点p投影到的图像空间中的坐标。简单地说,对于某些校准C,该函数将每次激光返回时的深度不连续性总结为D的“边缘”的X倍。
Ideally, J would be optimized by performing a global search over all possible calibrations C. However, that six-dimensional space cannot be effectively searched in real time, and the objective function is not convex. Therefore, an online search for the optimal value of J is infeasible.
理想情况下,J将通过对所有可能的校准C执行全局搜索来优化。然而,无法实时有效地搜索六维空间,并且目标函数不是凸的。因此,在线搜索J的最佳值是不可行的.
However, despite that the global optimum of J is unobtainable in real time, it is possible to determine, with very high accuracy, whether a given C is correct to within a given threshold. For many classes of problem, it is often far simpler to discern whether a given solution to a problem is correct than it is to determine a correct solution from scratch. Indeed, the same holds here.
然而,尽管无法实时获得J的全局最优值,但可以以非常高的精度确定给定C是否在给定阈值内是正确的。对于许多类型的问题,辨别问题的给定解决方案是否正确通常比从头开始确定正确的解决方案简单得多。事实上,这里也是如此。
Just as a highly out-of-focus camera image is obviously not focused properly, even if the viewer cannot determine the precise distance that the camera should have been focused at, it is possible to determine that a proposed C is wrong even without knowing what the correct C is. In other words, whether or not J C J_C JC is a local optimum of J is a strong indication of whether C is correct. But why should that be, given that we know J not to be convex? The answer is that even though J is unlikely to have only one local optimum, the probability of any given wrong calibration C being one of those optima is extremely small.
正如高度失焦的相机图像显然没有正确聚焦一样,即使观看者无法确定相机应该聚焦的精确距离,也有可能在不知道正确的C是什么的情况下确定所建议的C是错误的。换句话说, J C J_C JC是否是J的局部最佳值,是C是否正确的有力指示。但既然我们知道J不是凸的,为什么要这样呢?答案是,即使J不太可能只有一个局部最优值,任何给定的错误校准C成为这些最优值之一的概率都非常小。
Given a calibration C, we can compute J C J_C JC very quickly. If we perform a grid search with radius 1, centered around a given C, across all 6 dimensions, we will compute 3 6 = 729 3^6 = 729 36=729 different values of J (one of which will be J C J_C JC itself; that is, the center of the grid).3 Let F C F_C FC be the fraction of the 728 perturbed values of J that are worse than J C J_C JC . For example, if all 728 perturbations of C result in values of J worse than J C J_C JC , F C F_C FC would be 1. If half of the 728 perturbations of C result in values of J worse than J C J_C JC , F C F_C FC would be .5.
给定校准C,我们可以非常快速地计算 J C J_C JC。如果我们在所有6个维度上以给定C为中心执行半径为1的网格搜索,我们将计算 3 6 = 729 3^6=729 36=729不同的J值(其中一个值将是 J C J_C JC本身;即网格的中心)。设 F C F_C FC是728个J扰动值中比 J C J_C JC更差的一部分。例如,如果所有728个C扰动导致J值比 J C J_C JC差,则 F C F_C FC值为1。如果728个B扰动中有一半导致J值低于 J C J_C JC,则 F C F_C FC值为.5。
论文将离线标定的六个自由度变量中的每个自由度分别上下偏移一个浮动量,因此总共得到的离线标定1个 J c J_c Jc和其余728个浮动值得到的 J c J_c Jc。如果离线标定是准确的,那么离线标定得到的 J c J_c Jc是最大的,其余728个浮动值的 J c J_c Jc应该是小于离线标定得到的 J c J_c Jc的,因此再次构造一各个最终判定标量 F c F_c Fc,离线标定正确,那么 F c = 728 / 729 = 1 F_c = 728 /729 = 1 Fc=728/729=1.如果标定不准确,那么肯定会有浮动值的 J c J_c Jc大于离线标定的 J c J_c Jc,比如有一半的浮动值 J c J_c Jc大于离线标定的 J c J_c Jc,那么 F c = 364 / 729 = 0.5 F_c = 364/729=0.5 Fc=364/729=0.5。那么就需要通过搜寻算法寻找最大的 J c J_c Jc,那么最大的 J c J_c Jc对应的X,Y,Z,rpy就是正确的校正之后的转换矩阵.
The key idea is that when C is correct, most perturbations of C should lower the objective function J; after all, a perturbation of a correct calibration must not also be correct, and therefore, if our objective function is effective, it should be worse for inaccurate calibrations. On the other hand, if C is incorrect, there should be a very low chance that JC will be at a local maximum of J. We now show that this distinction is empirically true.
关键思想是,当C是正确的时,C的大多数扰动应该降低目标函数J;毕竟,正确校准的扰动也不一定是正确的,因此,如果我们的目标函数是有效的,那么对于不准确的校准,它会更糟。另一方面,如果C不正确,JC达到J的局部最大值的可能性应该很低。我们现在证明,这种区别在经验上是正确的。
Fig.5 plots, over a series of frames, what fraction of the 729 perturbations of C result in values of the objective function J that are worse than JC , for both the correct C and several incorrect choices of C. In other words, it plots FC for each of six different Cs across a series of frames. Our hypothesis is confirmed: the FC values for the correct calibration are significantly higher than those of the incorrect calibrations. If we only use a window size of 1 frame, i.e. w = 1, we see that the correct calibration (top blue curve) usually gives the best value of J out of all perturbations, and for all frames, at least 80% of perturbations result in a decrease of J. On the other hand, the other five curves are quite noisy, but on average approximately 50% of perturbations to those calibrations improve J.
图5绘制了一系列帧中,对于正确的C和几个错误的C选择,729个C扰动中的哪一部分导致目标函数J的值比JC更差。换句话说,它绘制了一组帧中六个不同C的FC。我们的假设得到证实:正确校准的FC值显著高于错误校准的FC。如果我们只使用1帧的窗口大小,即w=1,我们可以看到,正确的校准(顶部蓝色曲线)通常给出所有扰动中J的最佳值,并且对于所有帧,至少80%的扰动会导致J的降低。
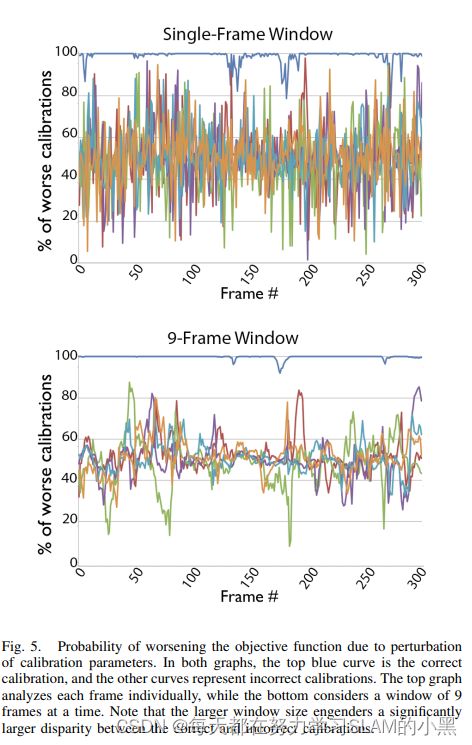
图5:校准参数扰动导致目标函数恶化的概率。在两个图中,顶部的蓝色曲线表示正确的校准,而其他曲线表示不正确的校准。顶部的图表分别分析每一帧,而底部的图表则考虑一次9帧的窗口。请注意,较大的窗口大小在正确和不正确的校准之间产生明显较大的差异。
Moving to a larger window size of 9 frames (which is just under one second of data at 10Hz), the two cases become significantly more disparate. Here, the correct calibration almost always gives the single best value of the objective function J, and no frame ever goes below FC = .9. At the same time, the incorrect values of C are now much more concentrated around FC = .5; both of these changes together make it even easier to disambiguate between the correct and incorrect case.
移动到9帧的更大窗口大小(在10Hz下仅为不到1秒的数据),这两种情况变得明显不同。这里,正确的校准几乎总是给出目标函数J的单个最佳值,并且没有一帧低于FC=.9。同时,错误的C值现在更集中在FC=.5附近;这两种变化加在一起,更容易消除正确和不正确情况之间的歧义。
We can also plot these data in a histogram, making it even more clear how distinct the two distributions are. In Fig.6, we see the distributions for the wrong calibrations on the left, and the correct calibrations on the right. It is readily apparent how different the two distributions are. Furthermore, we see that the top graphs, using a window size of 1 frame, are more similar to each other than the bottom graphs, which use a window size of 9 frames; this is expected, as the signal-to-noise ratio dramatically increases with the benefit of multiple frames.
我们还可以将这些数据绘制在直方图中,从而更加清楚这两种分布的区别。在图6中,我们在左侧看到错误校准的分布,在右侧看到正确校准的分布。很明显,这两种分布有多么不同。此外,我们看到,使用1帧窗口大小的顶部图比使用9帧窗口大小底部图彼此更相似;这是预期的,因为信噪比随着多帧的好处而显著增加。
These observations suggest a natural algorithm for determining whether the sensor is calibrated. Consider the two separate distributions of FC across a number of training frames, one for correct calibrations and the other for incorrect calibrations. We can fit a Gaussian to each of the two distributions, which then allows us to compute, for any value of FC , the probability that it was sampled from one distribution versus the other.4 Building the distributions from tens of incorrect calibrations (each generated by randomly perturbing the 6 calibration parameters) and one correct calibration on several hundred frames from each of several different logfiles, using a 9-frame window, we obtain a mean of µ1 = 99.7% and standard deviation of σ1 = 1.4 for correct calibrations, and a mean of µ2 = 50.5% and a standard devation of σ2 = 14 for incorrect calibrations.
这些观察结果表明了确定传感器是否校准的自然算法。考虑多个训练帧中FC的两个独立分布,一个用于正确校准,另一个用于错误校准。我们可以将高斯分布拟合到两个分布中的每一个,这样我们就可以计算FC的任何值,从一个分布对另一个分布采样的概率。4使用9帧窗口,从数十个错误校准(每个校准参数通过随机扰动6个校准参数生成)和数百个不同日志文件中的一个正确校准中构建分布,我们获得了正确校准的平均值µ1=99.7%和标准偏差σ1=1.4,对于不正确的校准,平均值µ2=50.5%,标准偏差σ2=14。
Therefore, using the standard formula for a Gaussian distribution, we can compute:
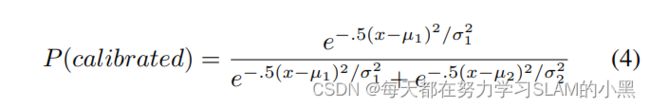 where P represents the probability that a calibration C having FC = x is a correct calibration. It is important to note that P is not a probability distribution over calibrations; rather, it is a statistical test which gives the probability of the observed data arising from a correctly calibrated sensor versus an incorrectly calibrated sensor
where P represents the probability that a calibration C having FC = x is a correct calibration. It is important to note that P is not a probability distribution over calibrations; rather, it is a statistical test which gives the probability of the observed data arising from a correctly calibrated sensor versus an incorrectly calibrated sensor
其中P表示具有FC=x的校准C是正确校准的概率。需要注意的是,P不是校准的概率分布;相反,这是一种统计测试,它给出了由正确校准的传感器与错误校准的传感器产生的观测数据的概率.
To be clear, although mathematically there is only exactly one calibration C which is actually “correct”, so that even an arbitrarily small deviation becomes “incorrect”, that is not the criteria used in this classification. Instead, the formula simply answers whether the sensors being calibrated or uncalibrated best explain the observed data, assuming each is equally likely a priori. Importantly, the tightness of the definition of correctness can be adjusted by changing σ1, while the tightness of the definition of incorrectness is controlled by σ2.
要清楚的是,尽管数学上只有一个校准C实际上是“正确”的,因此即使是任意小的偏差也会变得“不正确”,但这不是本分类中使用的标准。相反,该公式简单地回答了正在校准或未校准的传感器是否能最好地解释观测数据,假设每个传感器都有相同的先验可能性。重要的是,正确定义的严密性可以通过改变σ1来调整,而不正确定义的紧密性则由σ2控制。
Thus we have derived an easily computable formula that yields the probability that the robot’s current sensor calibration is accurate. Depending on the context, if this value falls below a designated threshold, a robot may choose to alert a command center, suspend its operation until further notice, or simply pause its activities to perform a more comprehensive offline calibration before resuming its work.
因此,我们导出了一个易于计算的公式,该公式得出了机器人当前传感器校准准确的概率。根据上下文,如果该值低于指定阈值,机器人可以选择向指挥中心发出警报,暂停其操作直到进一步通知,或者在恢复工作之前暂停其活动以执行更全面的离线校准。
IV. AUTOMATIC CALIBRATION TRACKING
In addition to determining whether a calibration is likely to be correct or not, we can also exploit the local convexity of the objective function J near the global optimum JC to track small changes in C over time.
除了确定校准是否正确,我们还可以利用目标函数J在全局最优JC附近的局部凸性来跟踪C随时间的微小变化。
If we consider all 729 perturbations of C from the grid search described in the previous section, some of them should be improvements if C is slightly incorrect. Of course, if C is wildly incorrect, there is no guarantee that ascending J will lead us in the right direction. However, if C is close to the right answer, gradient ascent would be expected to work. Our implementation is straightforward: at each iteration, the calibration C remains constant if all perturbations of C cause J to decrease, or else we select a new calibration C 0 which is the calibration out of all 729 candidates that gives the best value of J.
如果我们考虑上一节描述的网格搜索中C的所有729个扰动,如果C稍微不正确,其中一些扰动应该是改进的。当然,如果C是完全错误的,那么并不能保证上升的J会把我们引向正确的方向。然而,如果C接近正确答案,梯度上升将有望奏效。我们的实现很简单:在每次迭代中,如果C的所有扰动导致J减小,则校准C保持不变,否则我们从所有729个候选中选择一个新的校准C 0,这是给出J最佳值的校准。
Indeed, as we show in the results section, a slow and gradual adjustment of C in the direction of higher J does in fact allow us to track calibration changes over time. Unsurprisingly, the more frames that are used in the window, the better the signalto-noise ratio is. It is not realistic to expect a single-frame analysis to work all of the time, particularly in poorly-lit areas, areas with fewer 3D objects, or under severe flare or other artifacts. Instead, we find that a 9-frame analysis window is significantly more robust.
事实上,正如我们在结果部分所示,在较高J的方向上缓慢而渐进地调整C实际上允许我们跟踪校准随时间的变化。不出所料,窗口中使用的帧越多,信噪比就越好。期望单帧分析始终有效是不现实的,尤其是在光线较差的区域、3D对象较少的区域,或者在严重的光斑或其他伪影下。相反,我们发现9帧分析窗口明显更稳健。
As a consequence of a multi-frame window, we assume that the calibration changes within the window are negligible. For a window size of under a second, this should be a valid assumption in almost all scenarios.
作为多帧窗口的结果,我们假设窗口内的校准变化可以忽略不计。对于小于一秒的窗口大小,这在几乎所有场景中都应该是有效的假设。
V. EXPERIMENTAL RESULTS
For our experiments, we used a Velodyne HDL-64E S2 LIDAR sensor with 64 beams oriented between -22 and +2 degrees vertically and rotating 360 degrees horizontally. The unit spins at 10Hz and provides around 100,000 points per spin. The camera was a Point Gray Ladybug3 Panoramic unit with 5 separate cameras, of which we used just one for this paper. We ran the camera at 10Hz and used the middle third of the 1200x1600 vertical image, since the vertical field of view of the camera far exceeds that of our laser. The sensors were mounted to a vehicle equipped with an Applanix LV-420 GPS/IMU system, which was only used to adjust for local motion of the laser during each frame; no global coordinate frame or GPS coordinates were used, as the algorithms presented here do not require a globally consistent trajectory of the vehicle.
在我们的实验中,我们使用了Velodyne HDL-64E S2激光雷达传感器,该传感器具有64个垂直方向在-22度和+2度之间的光束,水平方向旋转360度。该装置以10Hz的频率旋转,每旋转一圈可提供约100000点。相机是一个点灰瓢虫3全景单元,有5个独立的相机,我们在本文中只使用了其中一个。我们以10Hz的频率运行相机,使用了1200x1600垂直图像的中间三分之一,因为相机的垂直视野远远超过我们的激光。这些传感器安装在一辆配备Applanix LV-420 GPS/IMU系统的车辆上,该系统仅用于调整每帧期间激光器的局部运动;没有使用全局坐标系或GPS坐标,因为这里提出的算法不需要车辆的全局一致轨迹。
VI. CONCLUSION
As robots move away from laboratory and factory settings and into real-life, unpredictable, and long-term operations, it is essential that sensor miscalibrations do not render them inoperable. A robot should be able to detect and correct errors in its calibration in real-time during operation, so that it can continue operating safely and effectively.
随着机器人从实验室和工厂环境转移到现实生活中的、不可预测的和长期的操作中,传感器的错误校准不会使其无法操作至关重要。机器人应能够在操作过程中实时检测和纠正校准中的错误,以便能够安全有效地继续操作。
In this paper, we have developed two new algorithms to assist robots equipped with cameras and lasers in the reliability of their perception systems over time. The constant background monitoring algorithm that detects sudden miscalibrations is an important tool for robots which need to know whether they can actually rely on the sensor data they’re receiving. While this is but one of many important checks a robot ought to perform on its sensor data, we believe it is an important, and perhaps underappreciated one.
在本文中,我们开发了两种新的算法,以帮助配备摄像机和激光器的机器人随着时间的推移提高其感知系统的可靠性。检测突然失准的恒定背景监控算法是机器人的一个重要工具,机器人需要知道自己是否能够真正依赖于所接收的传感器数据。虽然这只是机器人应该对其传感器数据进行的许多重要检查中的一项,但我们认为这是一项重要的检查,而且可能被低估了。
Additionally, we have shown that it is possible to track gradual drift of sensor pose over time, without performing computationally intensive global optimizations over the entire search space. This technique is suitable to be run in a background process, consuming very little CPU time, but potentially significantly improving the accuracy of a perception pipeline that includes camera-laser fusion. As expected, there is a tradeoff between the sensitivity with which minor miscalibrations can be detected and the number of frames required to make the determination. Yet even using less than one second of data, our results are more accurate than state-ofthe art offline techniques which require a calibration target [12] or hand-labeling of camera-laser correspondences [4].
此外,我们已经表明,可以跟踪传感器姿态随时间的逐渐漂移,而无需在整个搜索空间上执行计算密集型全局优化。该技术适合在后台过程中运行,消耗很少的CPU时间,但可能显著提高包括相机激光融合在内的感知管道的准确性。正如预期的那样,在可以检测到轻微错误校准的灵敏度和进行确定所需的帧数之间存在折衷。然而,即使使用不到1秒的数据,我们的结果也比最先进的离线技术更准确,离线技术需要校准目标[12]或手动标记相机激光对应关系[4]。
Further improvements in tracking accuracy and robustness should be possible by considering larger grid radii or by using a Monte Carlo sampling approach, such as a particle filter, rather than the greedy approach described here.
通过考虑更大的网格半径或使用蒙特卡洛采样方法(如粒子滤波器),而不是本文所述的贪婪方法,可以进一步提高跟踪精度和鲁棒性。
Although we focused on calibrating cameras to lasers in this paper, we hope that some of these insights will be useful to a variety of calibration tasks. In particular, the formation of a simple objective function that can discern the difference between a correctly and incorrectly calibrated sensor is often relatively straightforward, and from that starting point, many of the techniques discussed here should be readily applicable.
尽管我们在本文中专注于将相机校准为激光器,但我们希望其中的一些见解将对各种校准任务有用。特别是,能够辨别正确和错误校准的传感器之间的差异的简单目标函数的形成通常是相对简单的,并且从这个出发点出发,这里讨论的许多技术应该是容易适用的。