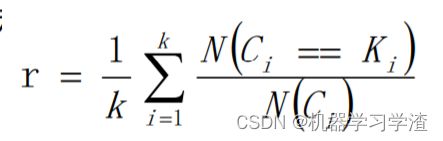K-Means和Mini Batch K-Means算法比较及效果评估案例

K-Means 和Mini Batch K-Means算法比较及效果评估案例

K-Means算法和Mini Batch K-Means算法已经由前两篇文章里讲述，这里不再赘述，请参考：Kmeans算法及简单案例 和 聚类优化算法——基于Kmeans算法

在写此案例之前我们先了解聚类算法的衡量指标

带y值的（实际中不常用）

1. 均一性：一个簇中只包含一个类别的样本，则满足均一性；其实也可以认为就是正确率(每个聚簇中正确分类的样本数占该聚簇总样本数的比例和
   

2. 完整性：同类别样本被归类到相同簇中，则满足完整性；每个聚簇中正确分类的样本数占该类型的总样本数比例的和——类似于召回率

3. V-measure：均一性和完整性的加权平均
   

4. Rand index(兰德指数)(RI)，RI取值范围为[0,1]，值越大意味着聚类结果与真实情况越吻合。
   
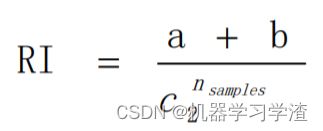
   其中C表示实际类别信息，K表示聚类结果，a表示在C与K中都是同类别的元素对数，b表示在C与K中都是不同类别的元素对数，$$c_2^{n_{samples}^{}}$$表示数据集中可以组成的对数

5. 调整兰德系数(ARI，Adjusted Rnd Index)，ARI取值范围[-1,1]，值越大，表示聚类结果和真实情况越吻合。从广义的角度来将，ARI是衡量两个数据分布的吻合程度的。
   

6. 调整互信息(AMI，Adjusted Mutual Information)，类似ARI，内部使用信息熵
   

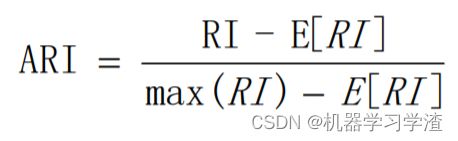
不带y值聚类衡量指标参考文章：聚类算法效果衡量标准

下面结合代码案例来分析K-Means和Mini Batch K-Means算法比较及效果评估

K-Means和Mini Batch K-Means算法比较

目的：基于scikit包中的创建模拟数据的API创建聚类数据，使用K-means算法和Mini Batch K-Means算法对数据进行分类操作，比较这两种算法的聚类效果以及聚类的消耗时间长度

# 导包
import time  
import numpy as np  
import matplotlib.pyplot as plt  
import matplotlib as mpl
from sklearn.cluster import MiniBatchKMeans, KMeans  
from sklearn.metrics.pairwise import pairwise_distances_argmin  
from sklearn.datasets.samples_generator import make_blobs  

## 设置属性防止中文乱码
mpl.rcParams['font.sans-serif'] = [u'SimHei']
mpl.rcParams['axes.unicode_minus'] = False

#初始化三个中心
centers = [[1, 1], [-1, -1], [1, -1]] 
clusters = len(centers)  #聚类的数目为3    
#产生3000组二维的数据，中心是意思三个中心点，标准差是0.7
X, Y = make_blobs(n_samples=3000, centers=centers, cluster_std=0.7, random_state=28)  

#构建kmeans算法
k_means = KMeans(init='k-means++', n_clusters=clusters, random_state=28)
t0 = time.time() #当前时间
k_means.fit(X)  #训练模型
km_batch = time.time() - t0  #使用kmeans训练数据的消耗时间
print ("K-Means算法模型训练消耗时间:%.4fs" % km_batch)
# 结果 K-Means算法模型训练消耗时间:0.0349s

#构建MiniBatchKMeans算法
batch_size = 100
mbk = MiniBatchKMeans(init='k-means++', n_clusters=clusters, batch_size=batch_size, random_state=28)  
t0 = time.time()  
mbk.fit(X)  
mbk_batch = time.time() - t0  
print ("Mini Batch K-Means算法模型训练消耗时间:%.4fs" % mbk_batch)
# 结果 Mini Batch K-Means算法模型训练消耗时间:0.0219s

#预测结果
km_y_hat = k_means.predict(X)
mbkm_y_hat = mbk.predict(X)

print(km_y_hat[:10])  # 前十个聚类预测值（簇）
print(mbkm_y_hat[:10])
print(k_means.cluster_centers_) # 聚类中心点
print(mbk.cluster_centers_)
# 结果
''' [0 2 2 2 2 1 0 0 2 2]
 [1 0 0 0 0 2 1 1 0 0]
 [[-1.0600799  -1.05662982]
  [ 1.02975208 -1.07435837]
 [ 1.01491055  1.02216649]]
[[ 0.99602094  1.10688195]
 [-1.00828286 -1.05983915]
 [ 1.07892315 -0.94286826]]'''

##获取聚类中心点并聚类中心点进行排序
k_means_cluster_centers = k_means.cluster_centers_#输出kmeans聚类中心点
mbk_means_cluster_centers = mbk.cluster_centers_#输出mbk聚类中心点
print ("K-Means算法聚类中心点:\ncenter=", k_means_cluster_centers)
print ("Mini Batch K-Means算法聚类中心点:\ncenter=", mbk_means_cluster_centers)
order = pairwise_distances_argmin(k_means_cluster_centers,  
                                  mbk_means_cluster_centers) # 遍历序列，求序列中距离的最小值，并返回其下标。
#方便后面画图
order
'''
K-Means算法聚类中心点:
center= [[-1.0600799  -1.05662982]
 [ 1.02975208 -1.07435837]
 [ 1.01491055  1.02216649]]
Mini Batch K-Means算法聚类中心点:
center= [[ 0.99602094  1.10688195]
 [-1.00828286 -1.05983915]
 [ 1.07892315 -0.94286826]]
array([1, 2, 0], dtype=int64)'''

## 画图
plt.figure(figsize=(12, 6), facecolor='w')
plt.subplots_adjust(left=0.05, right=0.95, bottom=0.05, top=0.9) # 调整图表、画布间距
cm = mpl.colors.ListedColormap(['#FFC2CC', '#C2FFCC', '#CCC2FF']) # ListedColormap定制的是离散型色板，颜色会根据色板列表循环
cm2 = mpl.colors.ListedColormap(['#FF0000', '#00FF00', '#0000FF'])
#子图1：原始数据
plt.subplot(221)
plt.scatter(X[:, 0], X[:, 1], c=Y, s=6, cmap=cm, edgecolors='none')
plt.title(u'原始数据分布图')
plt.xticks(())
plt.yticks(())
plt.grid(True)
#子图2：K-Means算法聚类结果图
plt.subplot(222)
plt.scatter(X[:,0], X[:,1], c=km_y_hat, s=6, cmap=cm,edgecolors='none')
plt.scatter(k_means_cluster_centers[:,0], k_means_cluster_centers[:,1],c=range(clusters),s=60,cmap=cm2,edgecolors='none')
plt.title(u'K-Means算法聚类结果图')
plt.xticks(())
plt.yticks(())
plt.text(-3.2, 2.5,  'train time: %.2fms' % (km_batch*1000))  
plt.grid(True)
#子图三Mini Batch K-Means算法聚类结果图
plt.subplot(223)
plt.scatter(X[:,0], X[:,1], c=mbkm_y_hat, s=6, cmap=cm,edgecolors='none')
plt.scatter(mbk_means_cluster_centers[:,0], mbk_means_cluster_centers[:,1],c=range(clusters),s=60,cmap=cm2,edgecolors='none')
plt.title(u'Mini Batch K-Means算法聚类结果图')
plt.xticks(())
plt.yticks(())
plt.text(-3.2, 2.5,  'train time: %.2fms' % (mbk_batch*1000))  
plt.grid(True)

#
different = list(map(lambda x: (x!=0) & (x!=1) & (x!=2), mbkm_y_hat))
for k in range(clusters):  
    different += ((km_y_hat == k) != (mbkm_y_hat == order[k]))
identic = np.logical_not(different)
different_nodes = len(list(filter(lambda x:x, different)))

plt.subplot(224)
# 两者预测相同的
plt.plot(X[identic, 0], X[identic, 1], 'w', markerfacecolor='#bbbbbb', marker='.')  
# 两者预测不相同的
plt.plot(X[different, 0], X[different, 1], 'w', markerfacecolor='m', marker='.')  
plt.title(u'Mini Batch K-Means和K-Means算法预测结果不同的点')  
plt.xticks(())  
plt.yticks(())
plt.text(-3.2, 2.5,  'different nodes: %d' % (different_nodes))  

plt.show()

K-Means算法和Mini Batch K-Means算法效果评估

# 导包
import time
import numpy as np  
import matplotlib.pyplot as plt  
import matplotlib as mpl
from sklearn.cluster import MiniBatchKMeans, KMeans 
from sklearn import metrics
from sklearn.metrics.pairwise import pairwise_distances_argmin  
from sklearn.datasets.samples_generator import make_blobs  

## 设置属性防止中文乱码
mpl.rcParams['font.sans-serif'] = [u'SimHei']
mpl.rcParams['axes.unicode_minus'] = False

# 在实际工作中是人工给定的，专门用于判断聚类的效果的一个值
### TODO: 实际工作中，我们假定聚类算法的模型都是比较可以，最多用轮廓系数/模型的score api返回值进行度量；
### 其它的效果度量方式一般不用
### 原因：其它度量方式需要给定数据的实际的y值 ===> 当我给定y值的时候，其实我可以直接使用分类算法了，不需要使用聚类
centers = [[1, 1], [-1, -1], [1, -1]] 
clusters = len(centers)       

X, Y = make_blobs(n_samples=3000, centers=centers, cluster_std=0.7, random_state=28) 
print(Y)

# 结果 array([2, 0, 0, ..., 2, 2, 1])

# 构建KMeans模型
k_means = KMeans(init='k-means++', n_clusters=clusters, random_state=28)
t0 = time.time() 
k_means.fit(X)  
km_batch = time.time() - t0  
print ("K-Means算法模型训练消耗时间:%.4fs" % km_batch)
# 结果 K-Means算法模型训练消耗时间:0.0981s


# 构建MiniBatchKMeans模型
batch_size = 100
mbk = MiniBatchKMeans(init='k-means++', n_clusters=clusters, batch_size=batch_size, random_state=28)  
t0 = time.time()  
mbk.fit(X)  
mbk_batch = time.time() - t0  
print ("Mini Batch K-Means算法模型训练消耗时间:%.4fs" % mbk_batch)
# 结果 Mini Batch K-Means算法模型训练消耗时间:0.0460s

km_y_hat = k_means.labels_
mbkm_y_hat = mbk.labels_
print(km_y_hat) # 样本所属的类别
# 结果 [0 2 2 ... 1 1 0]

k_means_cluster_centers = k_means.cluster_centers_
mbk_means_cluster_centers = mbk.cluster_centers_
print ("K-Means算法聚类中心点:\ncenter=", k_means_cluster_centers)
print ("Mini Batch K-Means算法聚类中心点:\ncenter=", mbk_means_cluster_centers)
order = pairwise_distances_argmin(k_means_cluster_centers,  
                                  mbk_means_cluster_centers) 
order
'''
K-Means算法聚类中心点:
center= [[-1.0600799  -1.05662982]
 [ 1.02975208 -1.07435837]
 [ 1.01491055  1.02216649]]
Mini Batch K-Means算法聚类中心点:
center= [[ 0.99602094  1.10688195]
 [-1.00828286 -1.05983915]
 [ 1.07892315 -0.94286826]]
array([1, 2, 0], dtype=int64)'''


### 效果评估
score_funcs = [
    metrics.adjusted_rand_score,#ARI
    metrics.v_measure_score,#均一性和完整性的加权平均
    metrics.adjusted_mutual_info_score,#AMI
    metrics.mutual_info_score,#互信息
]

## 2. 迭代对每个评估函数进行评估操作
for score_func in score_funcs:
    t0 = time.time()
    km_scores = score_func(Y,km_y_hat)
    print("K-Means算法:%s评估函数计算结果值:%.5f；计算消耗时间:%0.3fs" % (score_func.__name__,km_scores, time.time() - t0))
    
    t0 = time.time()
    mbkm_scores = score_func(Y,mbkm_y_hat)
    print("Mini Batch K-Means算法:%s评估函数计算结果值:%.5f；计算消耗时间:%0.3fs\n" % (score_func.__name__,mbkm_scores, time.time() - t0))

# 结果
'''
K-Means算法:adjusted_rand_score评估函数计算结果值:0.72526；计算消耗时间:0.199s
Mini Batch K-Means算法:adjusted_rand_score评估函数计算结果值:0.72421；计算消耗时间:0.002s

K-Means算法:v_measure_score评估函数计算结果值:0.65754；计算消耗时间:0.011s
Mini Batch K-Means算法:v_measure_score评估函数计算结果值:0.65780；计算消耗时间:0.003s

K-Means算法:adjusted_mutual_info_score评估函数计算结果值:0.65726；计算消耗时间:0.026s
Mini Batch K-Means算法:adjusted_mutual_info_score评估函数计算结果值:0.65757；计算消耗时间:0.006s

K-Means算法:mutual_info_score评估函数计算结果值:0.72231；计算消耗时间:0.003s
Mini Batch K-Means算法:mutual_info_score评估函数计算结果值:0.72264；计算消耗时间:0.002s
'''