GMM_example(2)
若已知高斯混合模型的均值、协方差矩阵和权重系数,用函数gmdistribution可以生成一个高斯混合模型。通常我们只有一组样本数据,要将其拟合为高斯混合模型,所用算法为EM算法;matlab中函数fitmdist()可以较好的拟合出高斯混合模型。
实验代码如下:
%高斯混合模型的参数拟合
%产生三个二维的单高斯模型,并用来产生模拟数据
clc; close all; clear all;
k = 3; %单高斯成分个数
mu1 = [-2 -2]'; sigma1 = [1 0; 0 2]; %第一个高斯分布
mu2 = [-3 3]'; sigma2 = [1 0; 0 0.5]; %第二个高斯分布
mu3 = [ 3 -3]'; sigma3 = [0.5 0; 0 1]; %第三个高斯分布
%根据三个高斯模型参数,分别随机产生500个样本点,并组合在一起
rng(1);
X1 = mvnrnd(mu1,sigma1,500); %产生第一类样本数据
X2 = mvnrnd(mu2,sigma2,500); %产生第二类样本数据
X3 = mvnrnd(mu3,sigma3,500); %产生第三类样本数据
X = [X1; X2; X3]; %组成三类样本数据
gm = fitgmdist(X,k); %gm是个结构体,保存了拟合模型的参数
lab = [ones(500,1);2*ones(500,1);3*ones(500,1)]; %三类数据的标签
h = gscatter(X(:,1), X(:,2), lab); %画出三类数据散点图
hold on;
f = @(x,y)pdf(gm,[x,y]); %计算拟合后的概率密度函数值
fcontour(f, '--', 'LineWidth',2);
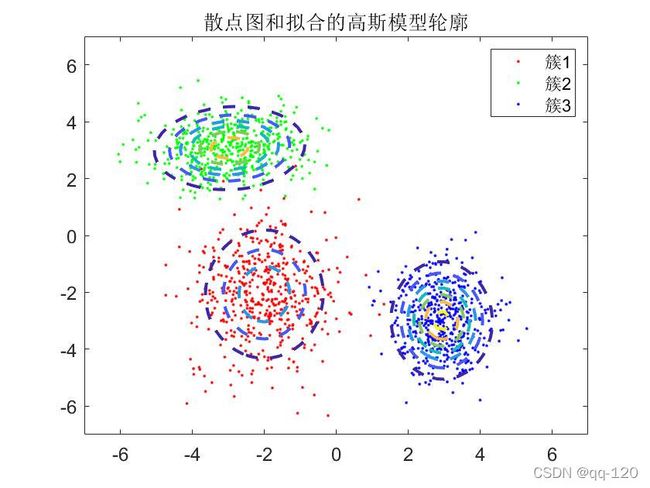
title('散点图和拟合的高斯模型轮廓');
legend('簇1','簇2','簇3','Location','NE');
set(gca,'Ylim',[-7,7],'Xlim',[-7,7],'FontSize',12);
hold off
properties(gm) %显示拟合模型的属性
Mu = gm.mu %显示拟合模型的均值
Sigma = gm.Sigma %显示拟合模型的协方差
w = gm.ComponentProportion %显示拟合模型的成分比例
其输出为
Mu =
2.9313 -2.9883
-1.9967 -2.0620
-2.9637 3.0801
Sigma(:,:,1) =
0.4878 -0.0162
-0.0162 1.0621
Sigma(:,:,2) =
0.9857 0.0049
0.0049 1.8753
Sigma(:,:,3) =
1.1347 0.0667
0.0667 0.5450
w =
0.3345 0.3307 0.3348
其中w为三种数据的混合比例,Mu为均值,Sigma为协方差矩阵,可见其拟合效果还不错。
%高斯混合聚类实例
%------生成两类高斯样本用于拟合与聚类----------------%
rng default %可重复性
mu1 = [1,2]; sigma1 = [3 0.2;0.2 2]; %第一个高斯分布参数
mu2 = [-1,-2]; sigma2 = [2 0; 0 1]; %第二个高斯分布参数
X1 = mvnrnd(mu1,sigma1,300); %生成第一个高斯样本数据
X2 = mvnrnd(mu2,sigma2,300); %生成第二个高斯样本数据
X = [X1; X2]; %组装成总样本数据
Y = [ones(300,1); 2*ones(300,1)]; %贴上标签
n = size(X,1); %矩阵X的行数
figure (1)
gscatter(X(:,1), X(:,2),Y,'rb','*x'); %原始数据散点图
title('原始数据'); xlabel('x'); ylabel('y');
set(gca,'Fontsize',12); %设置字体大小
%--------------拟合已生成的高斯样本--------------------%
figure (2)
%可选参数设置
options = statset('Display','final');
gm = fitgmdist(X,2,'Options',options); %拟合模型参数 %画出拟合模型的投影散点图
gscatter(X(:,1), X(:,2),Y,'rb','*x'); %原始样本散点图
hold on; %将拟合结果叠加到散点图
fcontour(@(x,y)pdf(gm,[x,y]),[-6,6,-6,6]); %等位线图
title('散点图和拟合GMM模型');

在得到拟合的高斯混合模型之后, 就可以用高斯混合聚类的的 cluster 方法来对数
据进行硬聚类;
%-----------利用cluster方法进行聚类-----------------%
idx = cluster(gm,X); %得到拟合数据的标签
esti_label = idx; %赋值给一个新变量
k = find(esti_label~=Y); %找到拟合标签与真实标签不符的样本
idx(k)=3; %标记错误分类的点为数字3
figure (3);
gscatter(X(:,1),X(:,2),idx,'rbk','*xo');
legend('簇1','簇2','簇3','Location','NW');
title('高斯混合聚类聚类');

图中的红色点和蓝色点分别代表类别为 1 和 2 的样本点, 黑色点表示分错的样本点。从图中可以直观地看出利用高斯混合聚类能够获得很高的分类正确率。
计算后验概率. 利用高斯混合聚类不仅能够对每个样本分类, 实际上还可 以算出每个样本点对各个类别的后验概率, 即隶属度. 可以用函数 posterior() 这一工作;
%------------------计算后验概率----------------------%
w = posterior(gm,X); %计算拟合模型的后验概率
%w是n*2矩阵,每一行是一个样本点,每一列代表对于两个类的隶属度大小
clus1 = (idx==1); %簇1的标签
clus2 = (idx==2); %簇2的标签
figure(4)
scatter(X(clus1,1),X(clus1,2),14,w(clus1,1),'*'); %簇1 Scatter plot with points of size 14
hold on; box on;
scatter(X(clus2,1),X(clus2,2),14,w(clus2,2),'p'); %簇2 Scatter plot with points of size 14
hold off
clrmap = jet(80); %加上颜色条
colormap(clrmap(9:72,:));
ylabel(colorbar,'Probability Density Function'); %后验概率
title('隶属簇1的后验概率');
legend('簇1','簇2');

上图中越接近红色表示属于类别 1、2 的概率越大,相反,越接近蓝色表示属于类别 1、2 的概率越小。 可以看出对于上下边缘的数据都有明确的类别标签, 而对于中间分界处数据就有些模凌两可,因为它们属于两个类别的概率都很大。这也就是这个区域的数据容易分错的原因。
那如果有一批新的数据点,不在训练集合中,那么高斯混合聚类的效果如何呢?
%------------------对新样本数据的测试-------------------%
figure(5)
w = [0.6,0.4]; %设置权重系数
Mu = [mu1;mu2];
Sigma = cat(3,sigma1,sigma2);
gm1 = gmdistribution(Mu,Sigma,w); %生成一个高斯混合模型
X0 = random(gm1,100); %产生100个测试点
[idx0,~,p0] = cluster(gm,X0);
fcontour(@(x,y)pdf(gm,[x,y]),[min(X0(:,1)),max(X0(:,1)),min(X0(:,2)),max(X0(:,2))]);
hold on;
gscatter(X0(:,1),X0(:,2),idx0,'rb','*p');
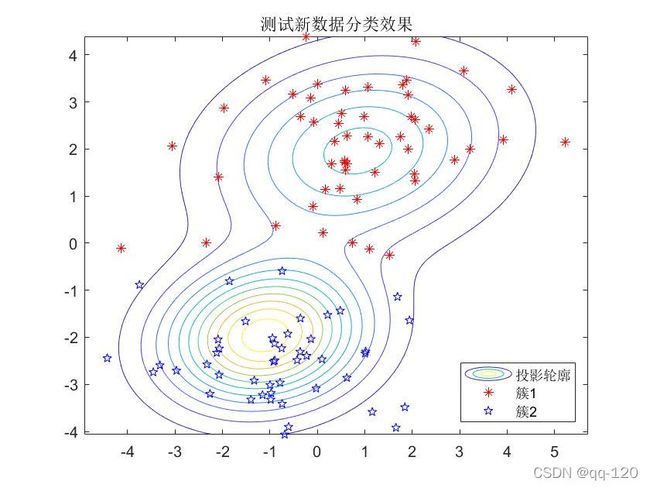
legend('投影轮廓','簇1','簇2','Location','SE');
title('测试新数据分类效果');