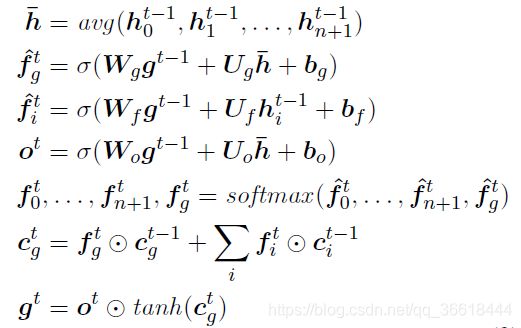当GNN遇见NLP(五) Sentence-State LSTM for Text Representation,ACL2018 +核心代码详解(pytorch)
本文作者来自Singapore University of Technology and Design以及Department of Computer Science, University of Rochester。
虽然本文中没有提到图神经网络的概念,但是从其实际操作上还是被归类为图的空间方法的一种。本文为了克服了BiLSTM局限于顺序文本的缺点,提出了新的模型S-LSTM,利用Recurrent steps在单词之间同时执行本地和全局信息交换,而不是对单词序列进行增量读取。换句话说,S-LSTM为LSTM增加了全局结点,并使用与LSTM同样的门规则对全局节点的信息进行更新,全局结点的信息也被用于与句子中的每一个单词结点进行信息交换,最终使得在减少了LSTM的复杂度的同时又提升了性能。
为了更深刻地理解本文,先复习一下LSTM。
LSTM
提到RNN,多数人都会想起来下边这样的图:
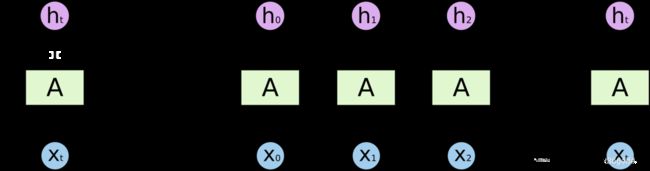
这里面的time step是指一句话的长度,每一个单词作为一个X输入,然后RNN的过程就是从头到尾遍历这句话的过程。每一个cell的输出对应X的输出,X+1个单词保留单词X的输出信息,这样就做到了记忆。但是可能由于梯度消失的原因,RNN的比较脑瘫,记忆力并不是很行,所以一个更强的版本LSTM诞生了。By the way,其实LSTM叫做(Long Short-Term Memory)长—短期记忆网络,而不是长短期—记忆网络。就跟北京的“东四-十条”不叫“东-四十条”一样。LSTM示意图如下:
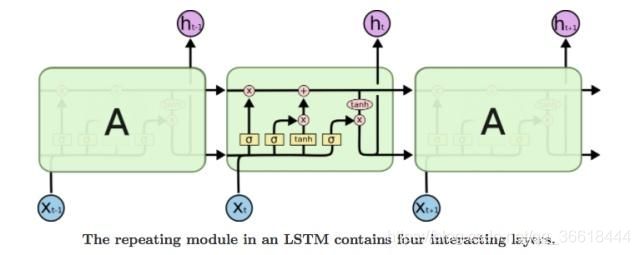
LSTM通过使用gate的机制(遗忘门,更新门,输出门)控制信息的取舍与更新,做到了更长时间的记忆。下面分别介绍这几个门。
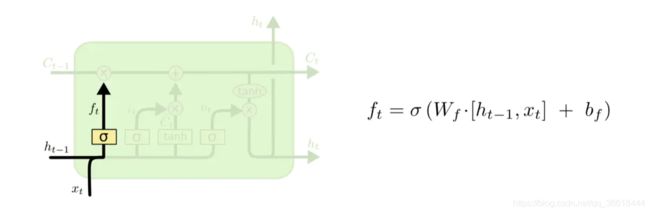
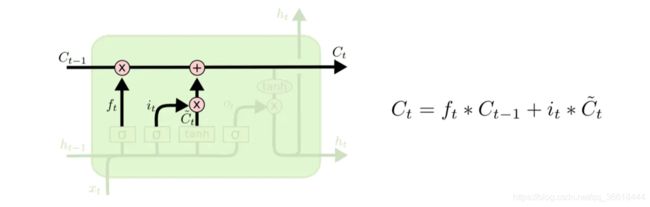
遗忘门:ht-1是上一个cell的输出,Ct-1表示上一个cell的状态。门本质上是一些列矩阵的操作,输出ft表示上一个cell的状态到底哪些要记住哪些要忘记。
更新门:决定了需要给本个cell的状态Ct添加哪些信息。

最终Ct由上一个cell的状态Ct-1和更新门的输出共同决定。
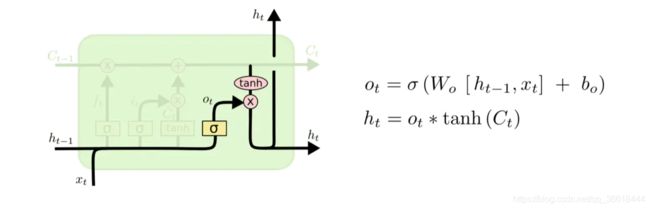
输出门:ot同样是一个参数矩阵乘法+bias然后过一个sigmoid激活函数的操作,最终cell的隐状态ht由ot与Ct共同参与决定。
本文Model

可以看到尽管S-LSTM脱胎于LSTM,但是与LSTM还是有一些差别:
- BiLSTM所需要的重复步骤的数量与句子的大小成比例,而S-LSTM所需的时间步是一个预设的参数,可以根据实际的实验进行调整。所以S-LSTM所需要的训练时间要比LSTM短。
- 句子级别结点g的添加。g^t在模型执行的过程中聚合整句话里所有单词结点的信息,并参与到下一层的结点的隐状态的更新的过程中。并且,句子级别的结点也可以被用来进行句子的分类。
- 每一个time step,单词wi都从上下文中聚合邻居单词的信息,这个领域的大小取决于窗口参数的大小,在后文中会对这个参数进行进一步探讨。假定每次传播从w_i-1和w_i+1两个结点聚合新的信息,在第二个time step就可以得到w_i-2和w_i+2的信息,因为w_i+1在第一个time step也从邻居聚合了有用的信息。因此随着time的增加,每个单词所聚合的上下文信息也越来越多,这就使得模型能够接受长距离的记忆。
从模型的实际传播过程也可以看出,S-LSTM尽管作用于一个序列(sentence),但是聚合方式以及全局结点的添加在本质上都属于GNN的基操。因此在清华大学孙茂松组发表的论文中将其归类为处理文本的GNN【1】。
github传送门:https://github.com/leuchine/S-LSTM
形式化描述
接下来就是枯燥的公式了。
第t步的S-LSTM状态可以表示为:
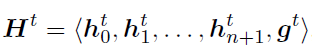
其中,h表示每个单词的隐藏状态表示,为啥有n+2个单词是因为在句首与句尾添加了两个特殊字符 < S>< /S> 表示句子的开始与结束。这两个字符的添加使得原本句子中第一个和最后一个单词也能参与到信息交换之中,因此会稍稍提升一下准确率。这个操作在后文的实验里也有提及。g则表示当前句子级别结点的隐藏信息。
之后句子中单词wi的信息更新的操作被表示为如下一大串公式。但是这些公式都和LSTM里的差不了多少,所以比较好理解:
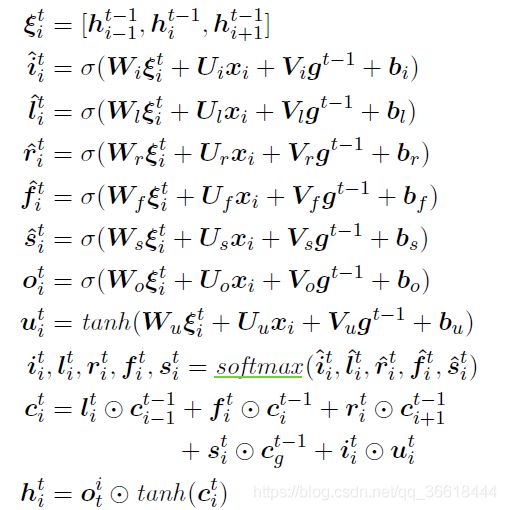
ξ:一个context window内的三个单词w_i-1,wi,w_i+1的隐状态的拼接。下面的公式都是依照这个ξ进行计算的。
i~:控制从输入xi获取到的信息,xi是单词的特征表示,可以是预训练的词向量。
l~:也就是left的门操作,控制从左侧单词w_i-1的cell接受到的信息
r~:同理,控制从右边的单词收到的信息。
f~:遗忘门,和LSTM中的遗忘门作用相同,控制从上一个时间步ct-1所得到的信息。
o~:输出门,来控制最终的输出。
u~:更新门
softmax:各种不同的门进行normalise
c~:当前节点对应cell的状态,由以上一大堆公式共同决定。
h~:最终的输出,输出还是由cell的状态与输出门共同控制。
然后恭喜你,你了解了文本结点是如何更新的,然后全局结点g还需要另一个cell进行更新。不过这个操作和以上操作差不多,相信你一看就会了:
实验
首先定义一下不同的任务。本文考虑了两种不同的任务:文本分类和序列标注。对于文本分类,可以使用全局结点作为softmax的输入:
![]()
最后一层隐藏层的结点信息可以应用在序列标注的任务中。当然,对于序列标注可以在输出层后边增加一层条件随机场(CRF)以提高准确率。
所有的损失函数都使用standard log-likelihood loss并添加L2正则化(正则化参数0.001)。
硬件以及超参数
因为实验中考虑到了模型的执行时间,因此要明确地说明硬件条件:GeForce GTX 1080 GPU with 8GB memory。
超参数上使用了预训练的Glove300,这个可以在Stanford的网站上下载预训练好的模型。Dropout为0.5,所有模型都使用Adam optimizer,初始learning rate为0.001并以0.97的速度进行衰减(0.001*0.97)。batch设置为10,每个sentence需要补全到同样的长度。
分类任务
可变超参数讨论
在MR数据集上进行了不同参数的实验。
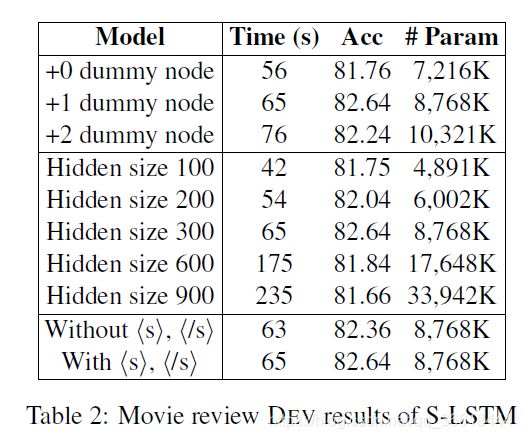
句子级别结点数(dummy node):1个最好。
Hidden Size:300
< S>:需要在句子首位两段添加特殊字符进行标记。
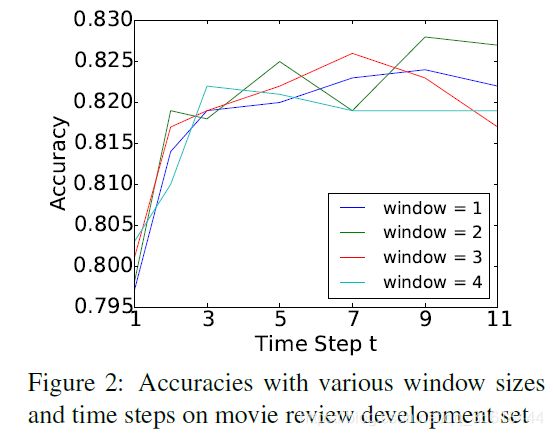
time step:step增加当然会让准确率一直有所提升,直到拟合。
window size:在较小的窗口大小下,可以使用更多的重复步骤来实现远程节点之间的信息交换,而在较大的窗口大小下,可以使用更少的步骤来实现。因此窗口的大小并不是很重要的参数。考虑到效率,剩余的实验选择窗口大小为1。step为9。
与LSTM、CNN以及Transform的比较

CNN的用时是一定最短的,这取决于模型的内部实现。LSTM要比S-LSTM长,这在前文也说了,LSTM需要每次都计算所有结点。在最终聚合w的信息到g的时候添加Attention有助于准确率的提升。
最终所有数据集比较
数据集描述:

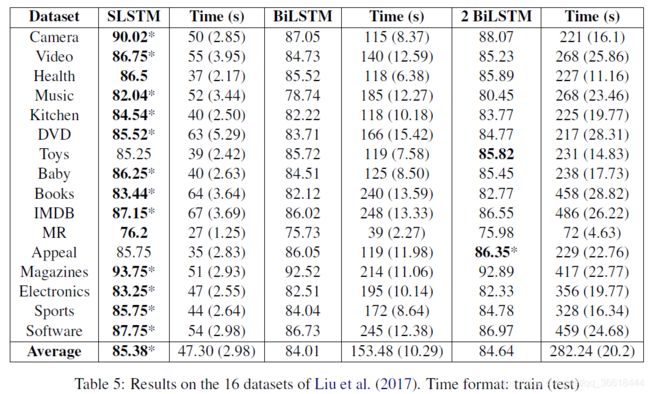
在16个数据集上有12个取得了最优的结果。
序列标注任务
使用了POS-tagging(词性标注)以及NER(命名实体识别)两个不同的子任务来验证。
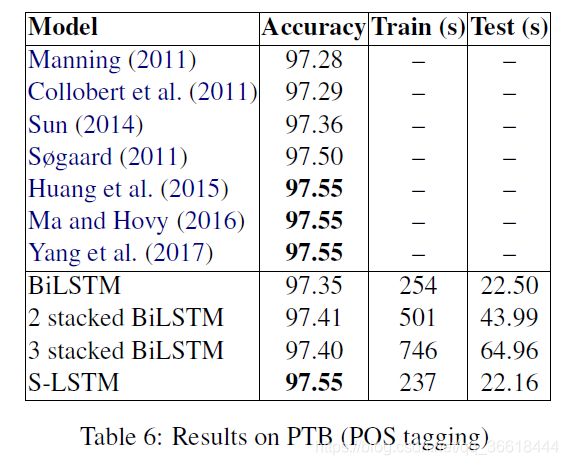
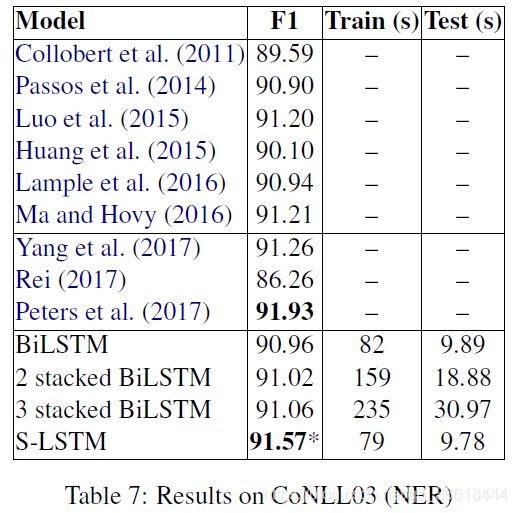
同时也实验了句子长度与准确率、耗时之间的关系:
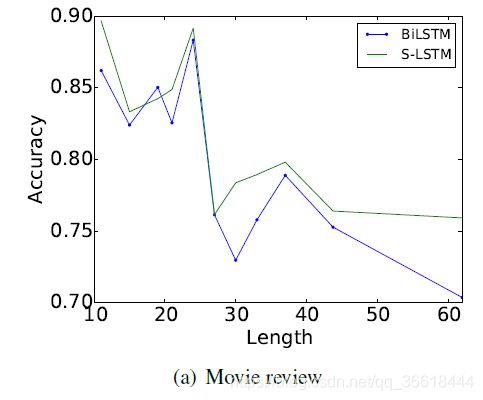
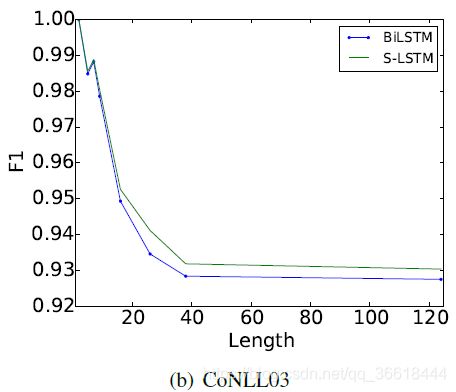
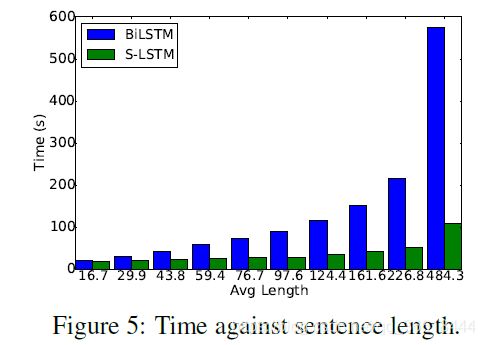
代码
代码的实现重点是门机制的实现,也就是对应文中的单词结点与句子结点的更新。总体的实现参考于https://github.com/WildeLau/S-LSTM_pytorch,略有改动。
首先,直接看sLSTM,这个实现了多个时间步的S-LSTM机制。需要明确其输入,是一个shape为batch,max sentence length,word2vec dim的三维张量。h_t对应t时刻hidden隐藏状态,c_t对应t时刻隐藏层状态。
class sLSTM(nn.Module):
r"""Args:
input_size: feature size of input sequence
hidden_size: size of hidden sate
window_size: size of context window
steps: num of iteration step
sentence_nodes:
bias: use bias if is True
batch_first: default False follow the pytorch convenient
dropout: elements are dropped by this probability, default 0
Inputs: (input, length), (h_0, c_0)
--input: (seq_len, batch, input_size)
--length: (batch, 1)
--h_0: (seq_len+sentence_nodes, batch, hidden_size)
--c_0: (seq_len+sentence_nodes, batch, hidden_size)
Outputs: h_t, g_t
--h_t: (seq_len, batch, hidden_size), output of every word in inputs
--g_t: (sentence_nodes, batch, hidden_size),
output of sentence node
"""
# step=7,全局结点数目1,窗口大小1表示只考虑wi的左右邻居
def __init__(self, input_size, hidden_size, window_size=1,
steps=7, sentence_nodes=1, bias=True,
batch_first=False, dropout=0):
super(sLSTM, self).__init__()
self.steps = steps
self.sentence_nodes = sentence_nodes
self.hidd = hidden_size
self.dense = nn.Linear(input_size, hidden_size) # dense to hidden
self.cell = sLSTMCell(input_size=hidden_size, hidden_size=hidden_size,
window_size=window_size,
sentence_nodes=sentence_nodes, bias=bias,
batch_first=batch_first, dropout=dropout)
def forward(self, x, hx=None):
x = x.permute(1,0,2) # reshape to seq_len, batch, hidden_size
if x.size()[-1] != self.hidd:
x = self.dense(x) # seq_len, batch, hidden_size
inputs = x
# inputs: (seqs, seq_lens)
if hx is None: # 对于t=0,h_t和c_t都是0向量
hidden_size = inputs[0].size()
# 结点数+全局结点,方便操作将全局结点和单词结点合并成一个张量
h_t = Variable(torch.zeros(hidden_size[0]+self.sentence_nodes,
hidden_size[1],
hidden_size[2]),
requires_grad=False).cuda()
c_t = Variable(torch.zeros_like(h_t.data), # c_t的shape与h_t相同
requires_grad=False).cuda()
else:
h_t = hx[0]
c_t = hx[1]
for step in range(self.steps): # cell对应论文中一个时间步的操作,通过循环的方式模拟steps
h_t, c_t = self.cell(x, (h_t, c_t))
h_x = h_t[:-self.sentence_nodes] # t时刻所有单词结点的隐状态,
h_g = h_t[-self.sentence_nodes:] # 全局结点的隐状态
return h_x, h_g, c_t
最基础的模块是sLSTMCell,输入是初始张量x,以及上一个时刻的h_t与c_t。sLSTMCell根据上一个cell的记忆对本cell进行更新。
class sLSTMCell(nn.Module):
r"""
Args:
input_size: feature size of input sequence
hidden_size: size of hidden state
window_size: size of context window
sentence_nodes:
bias: Default: ``True``
batch_first: default False follow the pytorch convenient
dropout: Default: 0
initial_mathod: 'orgin' for pytorch default
Inputs: (input, length), (h_0, c_0)
--input: (seq_len, batch, input_size)
--length: (batch, 1)
--h_0: (seq_len+sentence_nodes, batch, hidden_size)
--c_0: (seq_len+sentence_nodes, batch, hidden_size)
Outputs: (h_1, c_1)
--h_1: (seq_len+sentence_nodes, batch, hidden_size)
--c_1: (seq_len+sentence_nodes, batch, hidden_size)
"""
def __init__(self, input_size, hidden_size, window_size=1,
sentence_nodes=1, bias=True, batch_first=True,
dropout=0, initial_mathod='orgin'):
super(sLSTMCell, self).__init__()
self.input_size = input_size
self.hidden_size = hidden_size
self.window_size = window_size
self.num_g = sentence_nodes
self.initial_mathod = initial_mathod
self.bias = bias
self.batch_first = batch_first
self.dropout = dropout
self.lens_dim = 1 if batch_first is True else 0
self._all_gate_weights = []
# 单词结点对应的所有门参数定义
word_gate_dict = dict(
[('input gate', 'i'), ('lift forget gate', 'l'),
('right forget gate', 'r'), ('forget gate', 'f'),
('sentence forget gate', 's'), ('output gate', 'o'),
('recurrent input', 'u')])
# 通过循环的方式定义每个门所需的参数,每个不同的门都需要w,u,v,b四个参数
for (gate_name, gate_tag) in word_gate_dict.items():
# parameters named follow original paper
# weight: (out_features, in_features)
w_w = nn.Parameter(torch.Tensor(hidden_size,
(window_size*2+1)*hidden_size))
w_u = nn.Parameter(torch.Tensor(hidden_size, hidden_size))
w_v = nn.Parameter(torch.Tensor(hidden_size, hidden_size))
w_b = nn.Parameter(torch.Tensor(hidden_size))
gate_params = (w_w, w_u, w_v, w_b)
param_names = ['w_w{}', 'w_u{}', 'w_v{}', 'w_b{}']
param_names = [x.format(gate_tag) for x in param_names]
for name, param in zip(param_names, gate_params):
setattr(self, name, param)
self._all_gate_weights.append(param_names)
# parameters for sentence node,句子结点的参数定义方式相同,就是其参数少量一些
sentence_gate_dict = dict(
[('sentence forget gate', 'g'), ('word forget gate', 'f'),
('output gate', 'o')])
for (gate_name, gate_tag) in sentence_gate_dict.items():
# weight: (out_features, in_features)
s_w = nn.Parameter(torch.Tensor(hidden_size, hidden_size))
s_u = nn.Parameter(torch.Tensor(hidden_size, hidden_size))
s_b = nn.Parameter(torch.Tensor(hidden_size))
gate_params = (s_w, s_u, s_b)
param_names = ['s_w{}', 's_u{}', 's_b{}']
param_names = [x.format(gate_tag) for x in param_names]
for name, param in zip(param_names, gate_params):
setattr(self, name, param)
self._all_gate_weights.append(param_names)
# 参数初始化方案
self.reset_parameters(self.initial_mathod)
初始化参数的函数如下,如果参数全部默认设置为0可能造成梯度消失。
def reset_parameters(self, initial_mathod):
if initial_mathod is 'orgin':
std = 0.1
for weight in self.parameters():
weight.data.normal_(mean=0.0, std=std) # 平均数为0方差为0.1的标准正态分布
else:
stdv = 1.0 / math.sqrt(self.hidden_size)
for weight in self.parameters():
weight.data.uniform_(-stdv, stdv) # 将tensor用从均匀分布中抽样得到的值填充
在单词级别结点更新的时候需要考虑左右的结点,in_window_context对窗口内的结点进行聚合,聚合的方式(平均聚合还是向量拼接)根据不同的预设参数决定:
def in_window_context(self, hx, window_size=1, average=False): # average false表示使用张量拼接返回窗口内结点
slices = torch.unbind(hx, dim=0)
zeros = torch.unbind(Variable(torch.zeros_like(hx.data)), dim=0)
context_l = [torch.stack(zeros[:i] + slices[:len(slices)-i], dim=0)
for i in range(window_size, 0, -1)] # 窗口内左侧结点获取
context_l.append(hx)
context_r = [torch.stack(slices[i+1: len(slices)] + zeros[:i+1], dim=0)
for i in range(0, window_size)]
context = context_l + context_r
# average not concering padding. 0 also be averaged.
# official method is sum left and right respectivly and concat along
# hidden
return torch.stack(context).mean(dim=0) if average \
else torch.cat(context, dim=2)
最后是sLSTMCell的forward方法:
def forward(self, seqs, hx=None): # hx为None表示第一个cell
h_gt_1 = hx[0][-self.num_g:] # g数量*batch,dim
h_wt_1 = hx[0][:-self.num_g] # h表示隐藏状态,g是结点,w是单词
c_gt_1 = hx[1][-self.num_g:]
c_wt_1 = hx[1][:-self.num_g] # c表示cell的状态
# update sentence node
h_hat = h_wt_1.mean(dim=0) # nV处的平均,表示所有结点的平均值 batch*dim
# 1*batch*hidden + batch*hidden + batch*hidden broad cast = 1*batch*hidden
# 通过Linear模拟门的操作,本质上就是一个矩阵乘法。
# h_gt_1:句子级别结点t-1时刻的隐状态,fg对应结点级别的遗忘门
fg = F.sigmoid(F.linear(h_gt_1, self.s_wg) +
F.linear(h_hat, self.s_ug) + self.s_bg)
o = F.sigmoid(F.linear(h_gt_1, self.s_wo) + # o = 1*batch*hidden
F.linear(h_hat, self.s_uo) + self.s_bo)
fi = F.sigmoid(F.linear(h_gt_1, self.s_wf) +
F.linear(h_wt_1, self.s_uf) +
self.s_bf)
fi_normalized = F.softmax(fi, dim=0) # nV*batch*hidden
c_gt = fg.mul(c_gt_1).add(fi_normalized.mul(c_wt_1).sum(dim=0))
h_gt = o.mul(F.tanh(c_gt))
# 句子结点的更新结束
# update word nodes
epsilon = self.in_window_context(h_wt_1, window_size=self.window_size)
i = F.sigmoid(F.linear(epsilon, self.w_wi) +
F.linear(seqs, self.w_ui) +
F.linear(h_gt_1, self.w_vi) + self.w_bi)
l = F.sigmoid(F.linear(epsilon, self.w_wl) +
F.linear(seqs, self.w_ul) +
F.linear(h_gt_1, self.w_vl) + self.w_bl)
r = F.sigmoid(F.linear(epsilon, self.w_wr) +
F.linear(seqs, self.w_ur) +
F.linear(h_gt_1, self.w_vr) + self.w_br)
f = F.sigmoid(F.linear(epsilon, self.w_wf) +
F.linear(seqs, self.w_uf) +
F.linear(h_gt_1, self.w_vf) + self.w_bf)
s = F.sigmoid(F.linear(epsilon, self.w_ws) +
F.linear(seqs, self.w_us) +
F.linear(h_gt_1, self.w_vs) + self.w_bs)
o = F.sigmoid(F.linear(epsilon, self.w_wo) +
F.linear(seqs, self.w_uo) +
F.linear(h_gt_1, self.w_vo) + self.w_bo)
u = F.tanh(F.linear(epsilon, self.w_wu) +
F.linear(seqs, self.w_uu) +
F.linear(h_gt_1, self.w_vu) + self.w_bu)
gates = torch.stack((l, f, r, s, i), dim=0)
gates_normalized = F.softmax(gates, dim=0)
c_wt_l, c_wt_1, c_wt_r = \
self.in_window_context(c_wt_1).chunk(3, dim=2)
c_mergered = torch.stack((c_wt_l, c_wt_1, c_wt_r,
c_gt_1.expand_as(c_wt_1.data), u), dim=0)
c_wt = gates_normalized.mul(c_mergered).sum(dim=0)
h_wt = o.mul(F.tanh(c_wt))
# 每个单词结点更新结束
h_t = torch.cat((h_wt, h_gt), dim=0)
c_t = torch.cat((c_wt, c_gt), dim=0) # 单词级别结点和句子级别结点拼接后返回
return (h_t, c_t)
参考文献
【1】Zhou J, Cui G, Zhang Z, et al. Graph Neural Networks: A Review of Methods and Applications[J]. arXiv: Learning, 2018.