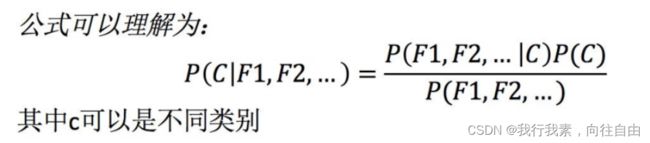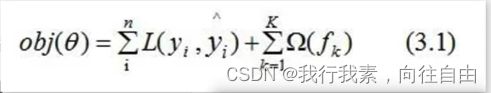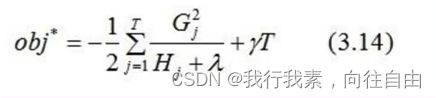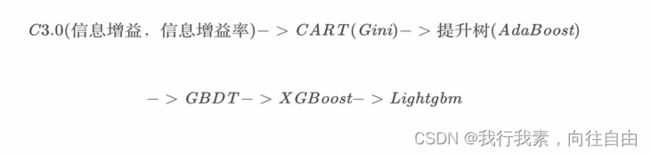机器学习之算法部分(算法篇2)
目录
1.朴素贝叶斯——分类算法
1.1 朴素贝叶斯算法简介
1.2 概率基础复习
1.2.1 概率定义
1.2.2 案例:判断女神对你的喜欢情况
1.2.3 联合概率、条件概率与相互独立
1.2.4 贝叶斯公式
1.2.5 小结
1.3 案例:商品评论情感分析
1.3.1 API介绍
1.3.2 商品评论情感分析
1.4 小结
2.支持向量机SVM——分类和回归
2.1 SVM算法简介
2.1.1 SVM算法导入
2.1.2 SVM算法定义
2.1.3 小结
2.2 SVM算法API初步使用
2.3 SVM算法原理
2.3.1 定义输入数据
2.3.2 线性可分支持向量机
2.3.3 SVM的计算过程与算法步骤
2.3.4 举例
2.4 SVM的损失函数
2.5 核方法
2.5.1 什么是核函数
2.5.2 常见核函数
2.5.3 小结
2.6 SVM回归
2.7 SVM算法api再介绍
2.7.1 SVM算法api综述
2.7.2 SVC【常用】
2.7.3 NuSVC
2.7.4 LinearSVC
2.7.5 小结
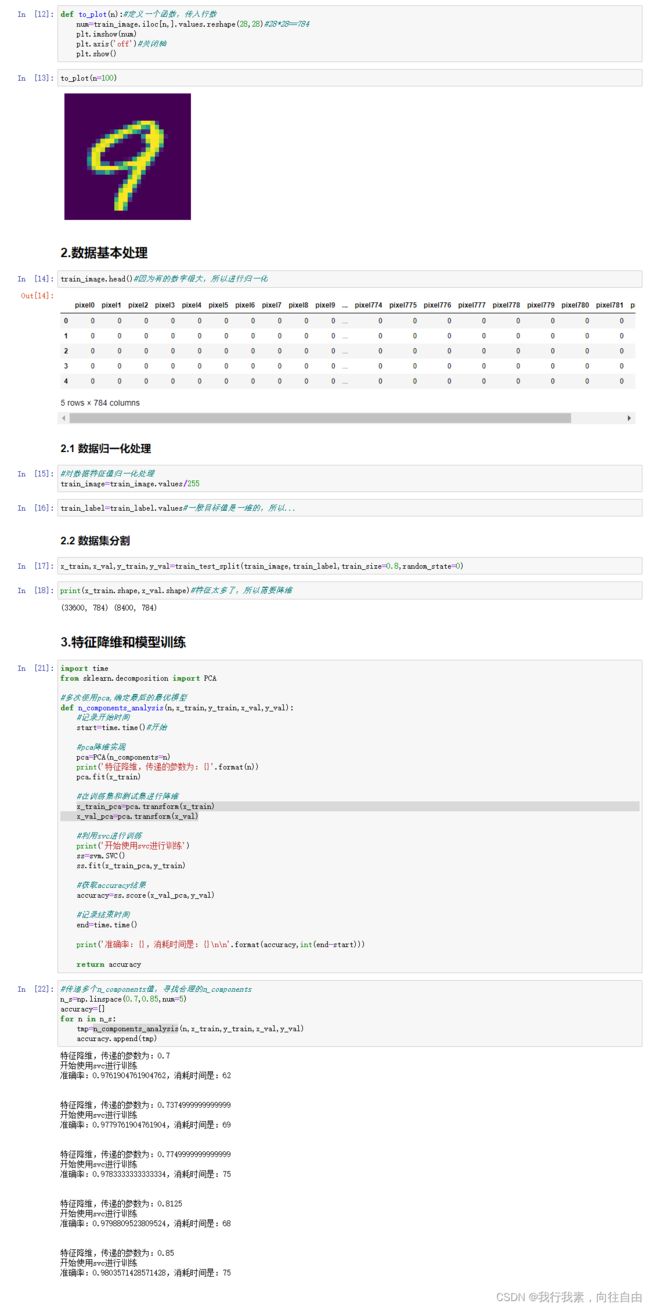
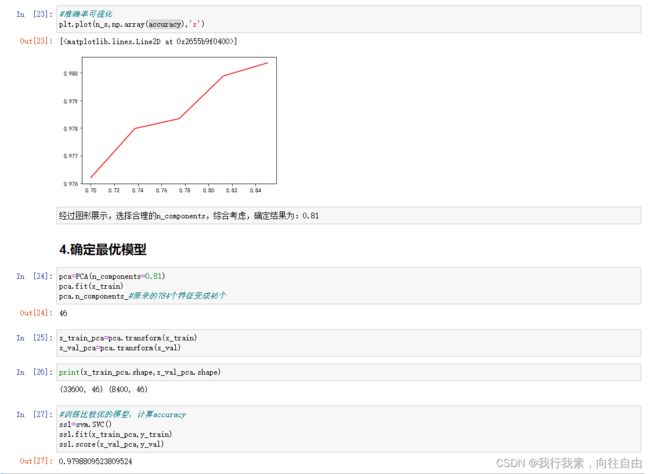
2.8 案例:数字识别器
2.8.1 案例背景介绍
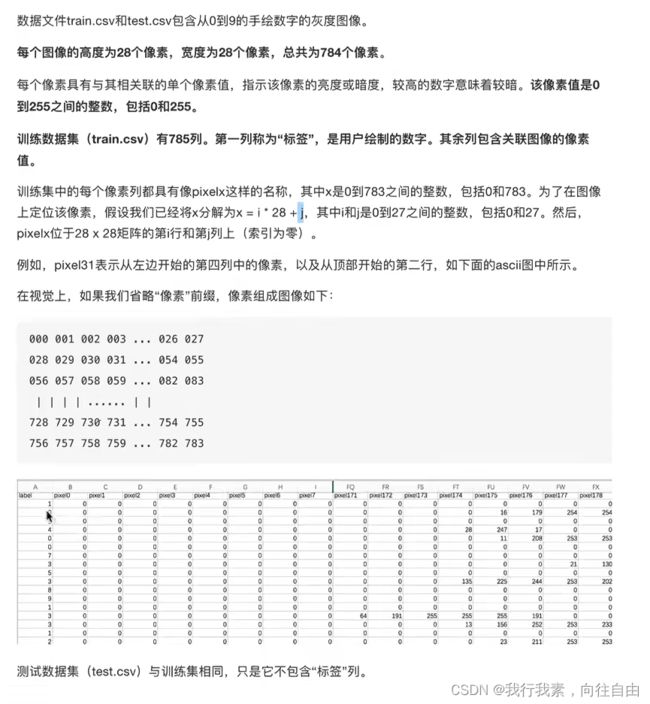
2.8.2 数据介绍
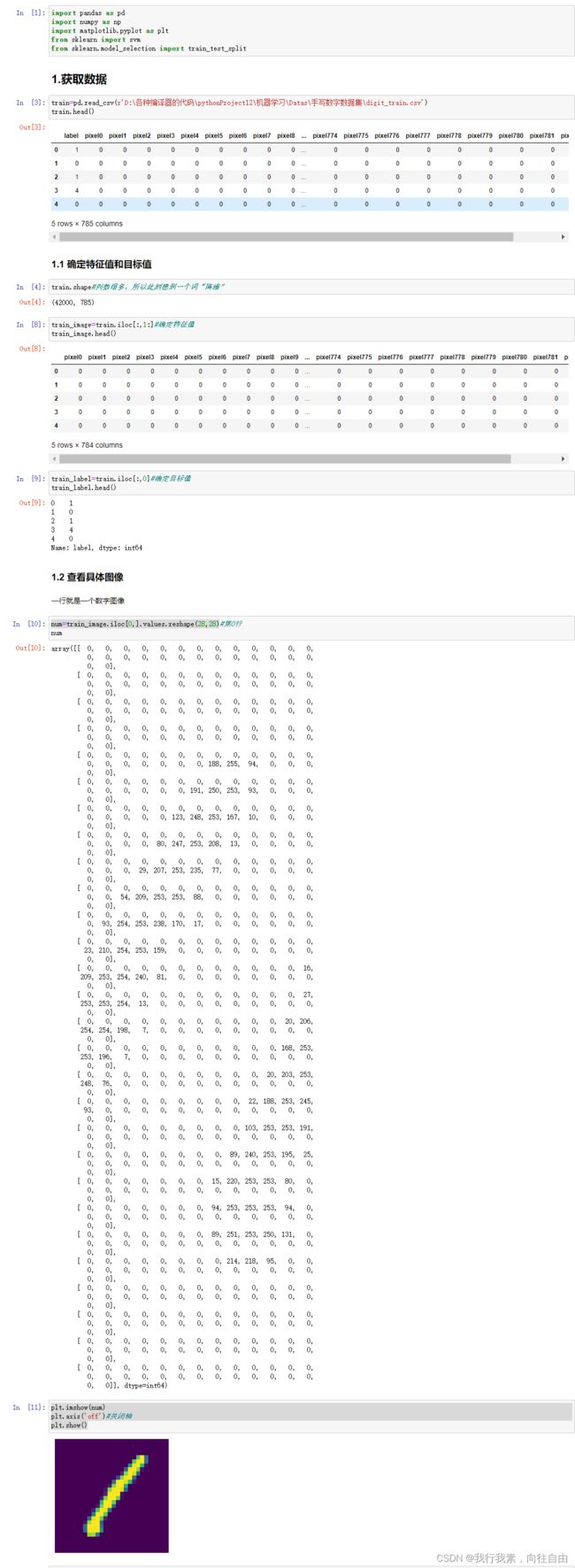
2.8.3 案例实现
2.9 总结
2.9.1 SVM基本综述
2.9.2 SVM优缺点
3.EM算法
3.1 初识EM算法
3.2 EM算法介绍
3.2.1 极大似然估计
3.2.2 EM算法实例描述
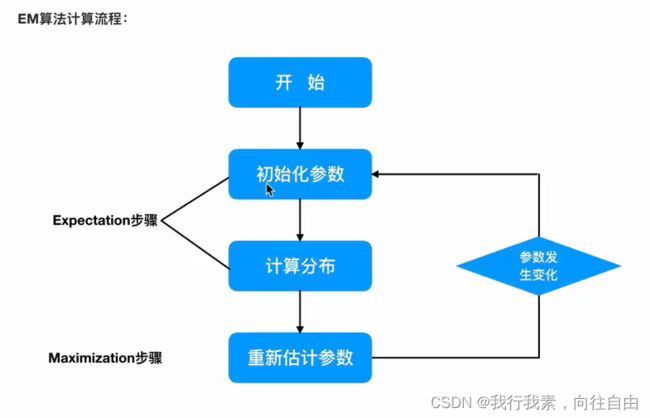
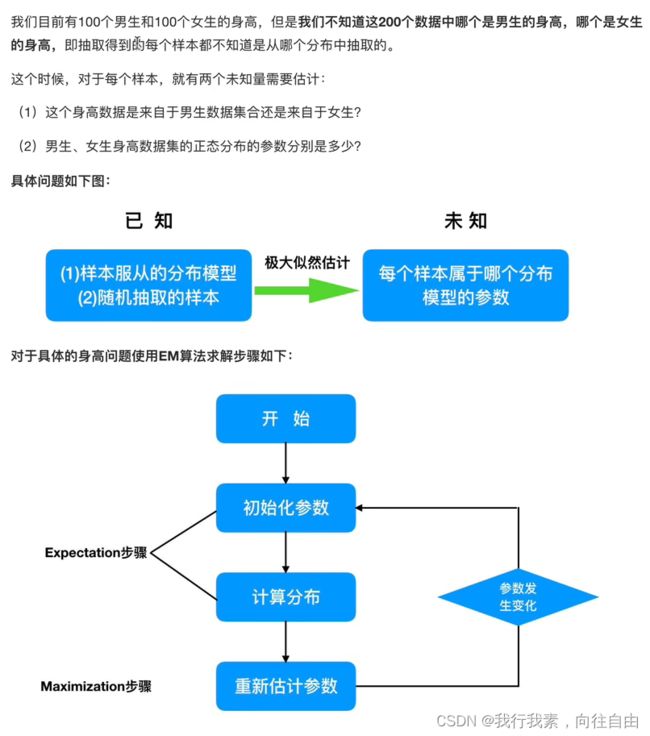
3.2.3 EM算法流程
3.3 EM算法实例
3.3.1 一个超级简单的案例
3.3.2 加入隐变量z后的求解
3.3.3 小结
4.HMM模型
4.1 马尔科夫链
4.1.1 简介
4.1.2 经典举例
4.1.3 小结
4.2 HMM简介
4.2.1 简单案例
4.2.2 案例进阶
4.2.3 小结
4.3 HMM模型基础
4.3.1 什么样的问题需要HMM模型
4.3.2 HMM模型的定义
4.3.3 一个HMM模型实例
4.3.4 HMM观测序列的生成
4.3.5 HMM模型的三个基本问题
4.3.6 小结
4.4 前向后向算法评估观察序列概率
4.4.1 回顾HMM问题一:求观测序列的概率
4.4.2 用前向算法求HMM观测序列的概率
4.4.3 HMM前向算法求解实例
4.4.4 用后向算法求HMM观测序列的概率【了解】
4.4.5 小结
4.5 维特比算法解码隐藏状态序列
4.5.1 HMM最可能隐藏状态序列求解概述
4.5.2 维特比算法概述
4.5.3 维特比算法流程总结
4.5.4 维特比算法求解实例
4.6 鲍姆-韦尔奇算法简介
4.6.1 鲍姆-⻙尔奇算法原理
4.7 HMM模型API介绍
4.7.1 API的安装
4.7.2 hmmlearn的介绍
4.7.3 MultinomialHMM实例
5.集成学习进阶——回归、分类
5.1 xgboost算法原理
5.1.1 最优模型的构建方法
5.1.2 XGBoost的目标函数推导
5.1.3 XGBoost的回归树构建方法
5.1.4 XGBoost与GDBT的区别
5.1.5 小结
5.2 xgboost算法api介绍
5.2.1 xgboost的安装
5.2.2 xgboost参数介绍
5.3 xgboost案例介绍
5.3.1 案例背景
5.3.2 步骤分析
5.3.3 代码实现
5.4 otto案例介绍 – Otto Group Product Classification Challenge【xgboost实现】
5.4.1 背景介绍
5.4.2 思路分析
5.4.3 代码实现
5.5 lightGBM
5.5.1 写在介绍lightGBM之前
5.5.2 什么是lightGBM
5.5.3 lightGBM原理
5.5.4 小结
5.6 lightGBM算法api介绍
5.6.1 lightGBM的安装
5.6.2 lightGBM参数介绍
5.6.3 调参建议
5.7 lightGBM案例介绍
5.8 《绝地求生》玩家排名预测
6.拓展知识
6.1 向量与矩阵的范数
6.1.1 向量的范数
6.1.2 矩阵的范数
6.2 朗格朗日乘子法
6.3 huber损失函数
6.4 极大似然函数取对数的原因
6.4.1 减少计算量
6.4.2 利于结果更好的计算
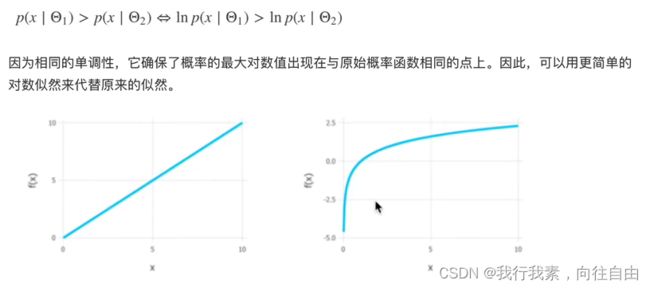
6.4.3 取对数并不影响最后结果的单调性
1.朴素贝叶斯——分类算法
学习目标
- 说明条件概率与联合概率
- 说明贝叶斯公式、以及特征独立的关系
- 记忆贝叶斯公式
- 知道拉普拉斯平滑系数
- 应用贝叶斯公式实现概率的计算
- 会使用朴素贝叶斯对商品评论进行情感分析
1.1 朴素贝叶斯算法简介
1.2 概率基础复习
学习目标
- 了解联合概率、条件概率和相关独立的概念
- 知道贝叶斯公式
- 知道拉普拉斯平滑系数
1.2.1 概率定义
- 概率定义:为⼀件事情发生的可能性
扔出⼀个硬币,结果头像朝上- P(X):取值在[0, 1]
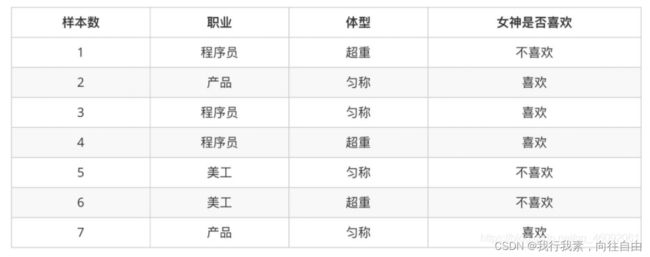
1.2.2 案例:判断女神对你的喜欢情况
在讲这两个概率之前我们通过⼀个例子,来计算⼀些结果:
问题如下:
- 女神喜欢的概率?
- 职业是程序员并且体型匀称的概率?
- 在女神喜欢的条件下,职业是程序员的概率?
- 在女神喜欢的条件下,职业是程序员、体重超重的概率?
计算结果为:
P(喜欢) = 4/7
P(程序员, 匀称) = 1/7(联合概率)
P(程序员|喜欢) = 2/4 = 1/2(条件概率)
P(程序员, 超重|喜欢) = 1/4
思考题:在小明是产品经理并且体重超重的情况下,如何计算小明被女神喜欢的概率?
即P(喜欢|产品, 超重) = ?
此时我们需要用到朴素贝叶斯进行求解,在讲解贝叶斯公式之前,首先复习⼀下联合概率、条件概率和相互独立的概念。
1.2.3 联合概率、条件概率与相互独立
- 联合概率:包含多个条件,且所有条件同时成立的概率
- 记作:P(A,B)
- 条件概率:就是事件A在另外⼀个事件B已经发生条件下的发生概率
- 记作:P(A|B)
- 相互独立:如果P(A, B) = P(A)P(B),则称事件A与事件B相互独立。
1.2.4 贝叶斯公式
(1)公式介绍
(2)案例计算
那么思考题就可以套用贝叶斯公式这样来解决:
P(喜欢|产品, 超重) = P(产品, 超重|喜欢)P(喜欢)/P(产品, 超重)
上式中,
- P(产品, 超重|喜欢)和P(产品, 超重)的结果均为0,导致无法计算结果。这是因为我们的样本量太少了,不具有代表性。
- 本来现实生活中,肯定是存在职业是产品经理并且体重超重的⼈的,P(产品, 超重)不可能为0;
- 而且事件“职业是产品经理”和事件“体重超重”通常被认为是相互独立的事件,但是,根据我们有限的7个样本计算 “P(产品, 超重) = P(产品)P(超重)”不成立。
而朴素贝叶斯可以帮助我们解决这个问题。
- 朴素贝叶斯,简单理解,就是假定了特征与特征之间相互独立的贝叶斯公式。
- 也就是说,朴素贝叶斯,之所以朴素,就在于假定了特征与特征相互独立。
所以,思考题如果按照朴素贝叶斯的思路来解决,就可以是:
P(产品, 超重) = P(产品) * P(超重) = 2/7 * 3/7 = 6/49 P(产品, 超重|喜欢) = P(产品|喜欢) * P(超重|喜欢) = 1/2 * 1/4 = 1/8 P(喜欢|产品, 超重) = P(产品, 超重|喜欢) P(喜欢)/P(产品, 超重) = 1/8 * 4/7 / 6/49 = 7/12
如果计算两个类别概率比较:所以我们只要比较前⾯的大小就可以,得出谁的概率大
(3)文章分类计算
需求:通过前四个训练样本(文章),判断第五篇文章,是否属于China类
计算结果:
P(C|Chinese, Chinese, Chinese, Tokyo, Japan) -->
P(Chinese, Chinese, Chinese, Tokyo, Japan|C) * P(C) / P(Chinese, Chinese, Chinese, Tokyo, Japan)
=
P(Chinese|C)^3 * P(Tokyo|C) * P(Japan|C) * P(C) / [P(Chinese)^3 * P(Tokyo) * P(Japan)]
# 这个⽂章是需要计算是不是China类,是或者不是最后的分⺟值都相同:
# ⾸先计算是China类的概率:
P(Chinese|C) = 5/8
P(Tokyo|C) = 0/8
P(Japan|C) = 0/8
# 接着计算不是China类的概率:
P(Chinese|C) = 1/3
P(Tokyo|C) = 1/3
P(Japan|C) = 1/3
# 这个⽂章是需要计算是不是China类:
⾸先计算是China类的概率: 0.0003
P(Chinese|C) = 5/8 --> 6/14
P(Tokyo|C) = 0/8 --> 1/14
P(Japan|C) = 0/8 --> 1/14
接着计算不是China类的概率: 0.0001
P(Chinese|C) = 1/3 -->(经过拉普拉斯平滑系数处理) 2/9
P(Tokyo|C) = 1/3 --> 2/9
P(Japan|C) = 1/3 --> 2/9
1.2.5 小结
1.3 案例:商品评论情感分析
学习目标
- 应用朴素贝叶斯API实现商品评论情感分析
1.3.1 API介绍
- sklearn.naive_bayes.MultinomialNB(alpha = 1.0)
- 朴素贝叶斯分类
- alpha:拉普拉斯平滑系数
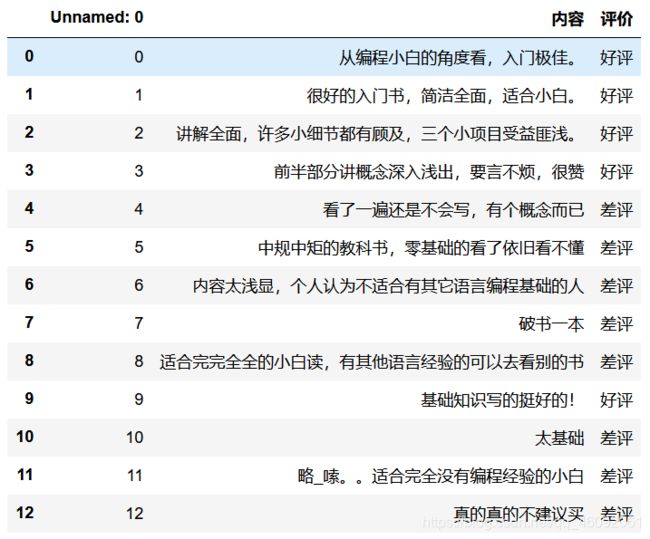
1.3.2 商品评论情感分析
(1)步骤分析
- 1)获取数据
- 2)数据基本处理
- 2.1) 取出内容列,对数据进行分析
- 2.2) 判定评判标准
- 2.3) 选择停⽤词
- 2.4) 把内容处理,转化成标准格式
- 2.5) 统计词的个数
- 2.6)准备训练集和测试集
- 3)模型训练
- 4)模型评估
(2)代码实现
import pandas as pd
import numpy as np
import jieba
import matplotlib.pyplot as plt
from sklearn.feature_extraction.text import CountVectorizer
from sklearn.naive_bayes import MultinomialNB
# 1. 获取数据(记得转换编码)
data = pd.read_csv("./data/commodity_comment/书籍评价.csv", encoding="gbk")
# 2. 数据基本处理
# 2.1 读取停用词文件【停用词来自网上,用于将一些没什么情感的词去除】
stop_words = []
with open('./data/commodity_comment/stopwords.txt', 'r', encoding='utf-8') as f:
lines = f.readlines() # 读取一行
for temp in lines:
line = temp.strip() # 去掉空格
stop_words.append(line) # 追加到停用词列表
# 由于文件来自网络,可能里面有重复词,所以先将其转换为set集合去重
stop_words = list(set(stop_words)) # 事实证明 用len()查看后,并没有重复的
# 2.2 把【内容】列转换成标准格式
comment_list = []
for temp in data["内容"]:
# temp是每一条内容,对它们进行分词处理
segment = jieba.cut(temp) # segment是分好词的对象
segment_str = ' '.join(segment) # 用空格分开每个词
comment_list.append(segment_str)
# 3. 特征工程 - 特征提取 中文文本提取,统计词的个数
# 3.1 加载停用词并实例化对象
count = CountVectorizer(stop_words=stop_words)
# 3.2 进行词数统计(可以得到所有内容中所有词的数量统计)
X = count.fit_transform(comment_list)
print("词:\n", count.get_feature_names()) # 打印所有词
print("统计:\n", X.toarray()) # 用toarray()转换为词频矩阵后,更容易观察,每一行就是一个评论,每一列对应一个词频
# 4. 数据分割。这一步骤以往是在 2.数据基本处理
# 用词频前10行作为训练集,后3行作为测试集
x_train = X.toarray()[:10, :]
y_train = (data["评价"].values)[:10] # 【评价】列是目标值,用前10作为训练集。values是只要值,没要行索引
x_test = X.toarray()[10:, :]
y_test = (data["评价"].values)[10:]
# 5. 模型训练
mnb = MultinomialNB()
mnb.fit(x_train, y_train)
# 6. 模型评估
print("预测值:", mnb.predict(x_test))
print("真实值:", y_test)
print("精确度:", mnb.score(x_test, y_test))
# 由于样本比较少,所以精确度能达到100%
#------------------------------------------------------------------------
# 我们可以对目标值【评价】进行01转换,好评为1,差评为0,并将其作为新列【评价标记】。
# 通常我们经常是用01来表示的,所以上面代码数据集划分处,可以用data['评价标记']代替
data.loc[data["评价"] == "好评", "评价标记"] = 1
data.loc[data["评价"] == "差评", "评价标记"] = 0
#------------------------------------------------------------------------
应用说明:百度AI情感倾向分析
1.4 小结
2.支持向量机SVM——分类和回归
2.1 SVM算法简介
2.1.1 SVM算法导入
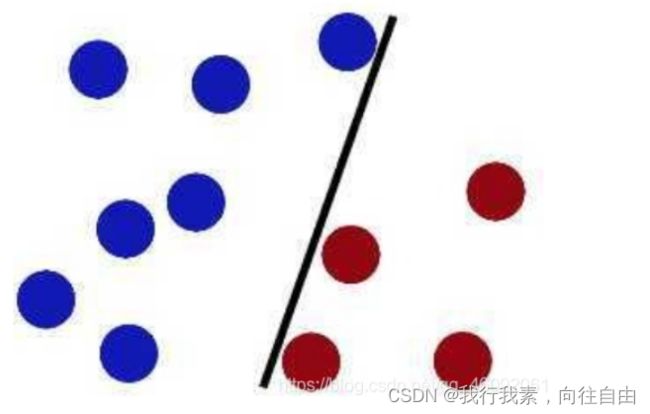
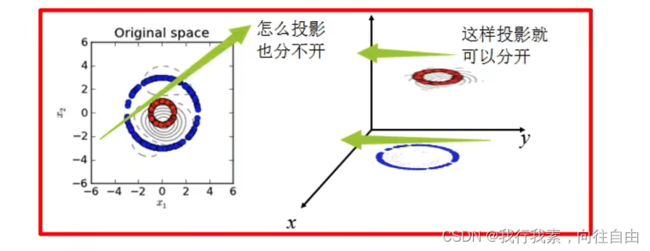
在很久以前的情⼈节,大侠要去救他的爱人,但魔鬼和他玩了⼀个游戏。
魔⻤在桌⼦上似乎有规律放了两种颜⾊的球,说:
“你⽤⼀根棍分开它们?要求:尽量在放更多球之后,仍然适⽤。
于是⼤侠这样放,⼲的不错?
怎么办?
把分解的⼩棍⼉变粗
SVM就是试图把棍放在最佳位置,好让在棍的两边有尽可能⼤的间隙。现在即使魔⻤放了更多的球,棍仍然是⼀个好的分界线。
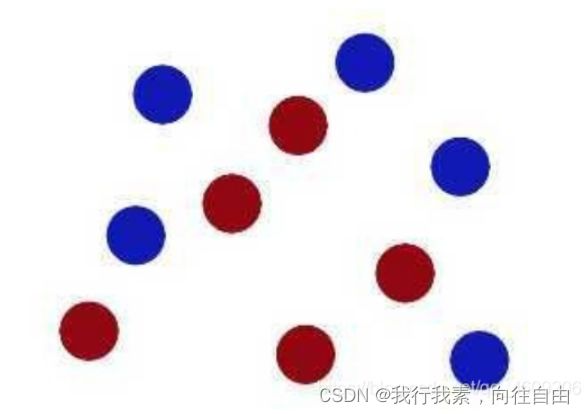
然后,在SVM ⼯具箱中有另⼀个更加重要的技巧( trick)。 魔⻤看到⼤侠已经学会了⼀个trick,于是魔⻤给了⼤侠⼀ 个新的挑战。
现在,⼤侠没有棍可以很好帮他分开两种球了,现在怎么办呢?
当然像所有武侠⽚中⼀样⼤侠桌⼦⼀拍,球⻜到空中。然后,凭借⼤侠的轻功,⼤侠抓起⼀张纸,插到了两种球的中间。
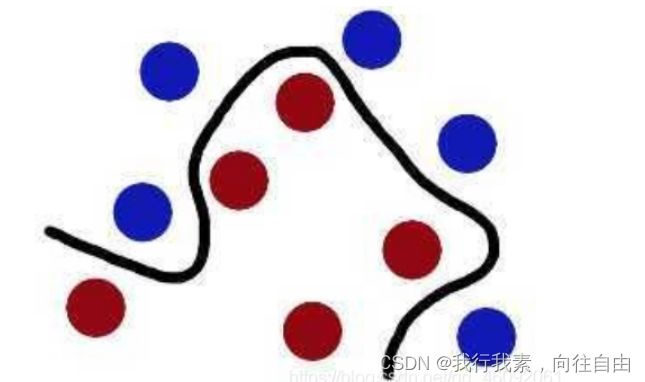
现在,从魔⻤的⻆度看这些球,这些球看起来像是被⼀条曲线分开了。
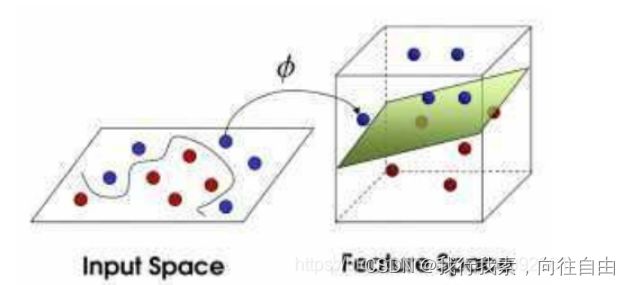
再之后,⽆聊的⼤⼈们,把上⾯的物体起了别名:
球—— 「data」数据
棍⼦—— 「classifier」分类
最⼤间隙——「optimization」最优化
拍桌⼦——「kernelling」核⽅法
纸——「hyperplane」超平⾯
案例来源:Support Vector Machines explained well | Byte Size Biology
⽀持向量机直观感受:https://www.youtube.com/watch?v=3liCbRZPrZA
2.1.2 SVM算法定义
(1)定义
SVM:SVM全称是supported vector machine(⽀持向量机),即寻找到⼀个超平⾯使样本分成两类,并且间隔最⼤。
SVM能够执⾏线性或⾮线性分类、回归,甚⾄是异常值检测任务。它是机器学习领域最受欢迎的模型之⼀。SVM特别适⽤于中⼩型复杂数据集的分类。
(2)超平面最大间隔介绍
- 上左图显示了三种可能的线性分类器的决策边界:
- 虚线所代表的模型表现⾮常糟糕,甚⾄都⽆法正确实现分类。其余两个模型在这个训练集上表现堪称完美,但是它们的决策边界与实例过于接近,导致在⾯对新实例时,表现可能不会太好。
- 右图中的实线代表SVM分类器的决策边界,不仅分离了两个类别,且尽可能远离最近的训练实例。
(3)硬间隔和软间隔
1.硬间隔分类
在上⾯我们使⽤超平⾯进⾏分割数据的过程中,如果我们严格地让所有实例都不在最⼤间隔之间,并且位于正确的⼀ 边,这就是硬间隔分类。
硬间隔分类有两个问题,⾸先,它只在数据是线性可分离的时候才有效;其次,它对异常值⾮常敏感。
当有⼀个额外异常值的鸢尾花数据:左图的数据根本找不出硬间隔,⽽右图最终显示的决策边界与我们之前所看到的⽆ 异常值时的决策边界也⼤不相同,可能⽆法很好地泛化。
2.软间隔分类
要避免这些问题,最好使⽤更灵活的模型。⽬标是尽可能在保持最⼤间隔宽阔和限制间隔违例(即位于最⼤间隔之上, 甚⾄在错误的⼀边的实例)之间找到良好的平衡,这就是软间隔分类。
- 在Scikit-Learn的SVM类中,可以通过超参数C来控制这个平衡:C值越⼩,则间隔越宽,但是间隔违例也会越多。上图显示了在⼀个⾮线性可分离数据集上,两个软间隔SVM分类器各⾃的决策边界和间隔。
- 左边使⽤了⾼C值,分类器的错误样本(间隔违例)较少,但是间隔也较⼩。
- 右边使⽤了低C值,间隔⼤了很多,但是位于间隔上的实例也更多。看起来第⼆个分类器的泛化效果更好,因为⼤多数间隔违例实际上都位于决策边界正确的⼀边,所以即便是在该训练集上,它做出的错误预测也会更少。
2.1.3 小结
2.2 SVM算法API初步使用
from sklearn import svm
x=[[0,0],[1,1]]
y=[0,1]
clf=svm.SVC()
clf.fit(x,y)
print(clf.predict([[2, 2]]))2.3 SVM算法原理
2.3.1 定义输入数据
2.3.2 线性可分支持向量机
2.3.3 SVM的计算过程与算法步骤
(1)推导目标函数
(2)目标函数的求解
到这⼀步,终于把目标函数给建立起来了。
那么下⼀步⾃然是去求目标函数的最优值.
因为⽬标函数带有⼀个约束条件,所以我们可以⽤拉格朗⽇乘⼦法求解。
1.朗格朗⽇乘⼦法
2.对偶问题
3.整体流程确定
2.3.4 举例
2.4 SVM的损失函数
2.5 核方法
2.5.1 什么是核函数
(1)核函数概念
(2)核函数举例
举例1:
举例2:
2.5.2 常见核函数
2.5.3 小结
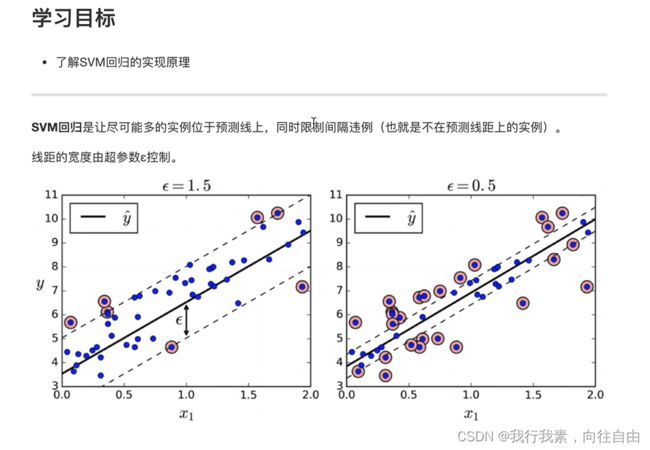
2.6 SVM回归
2.7 SVM算法api再介绍
![]()
2.7.1 SVM算法api综述
2.7.2 SVC【常用】
2.7.3 NuSVC
2.7.4 LinearSVC
2.7.5 小结
2.8 案例:数字识别器
2.8.1 案例背景介绍
2.8.2 数据介绍
2.8.3 案例实现
2.9 总结
2.9.1 SVM基本综述
2.9.2 SVM优缺点
3.EM算法
![]()
3.1 初识EM算法
3.2 EM算法介绍
3.2.1 极大似然估计
(1)问题描述
![]()
(2)用数学知识解决现实问题
(3)最大似然函数估计值的求解步骤
极大似然函数取对数的原因见后文6.4节。
3.2.2 EM算法实例描述
3.2.3 EM算法流程
3.3 EM算法实例
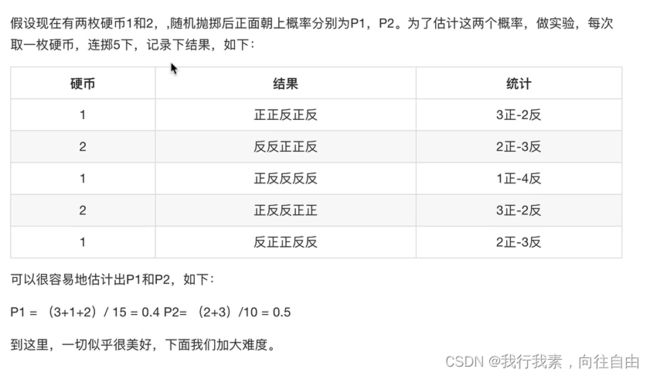
3.3.1 一个超级简单的案例
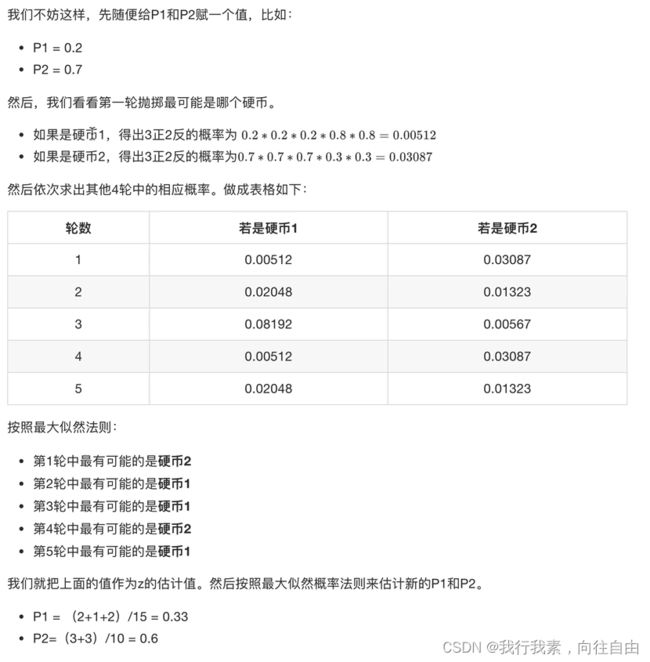
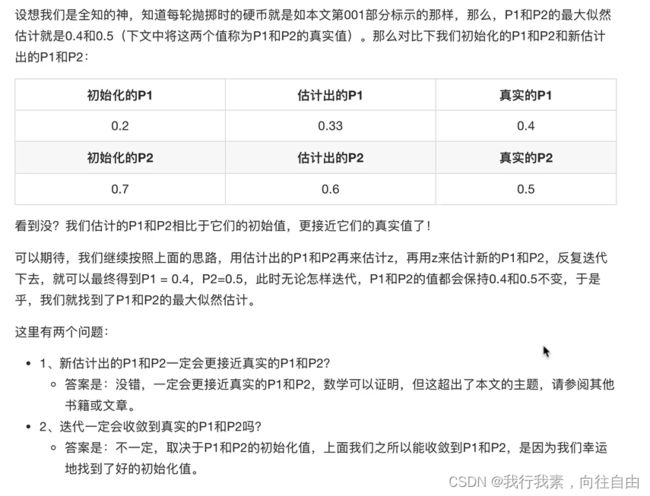
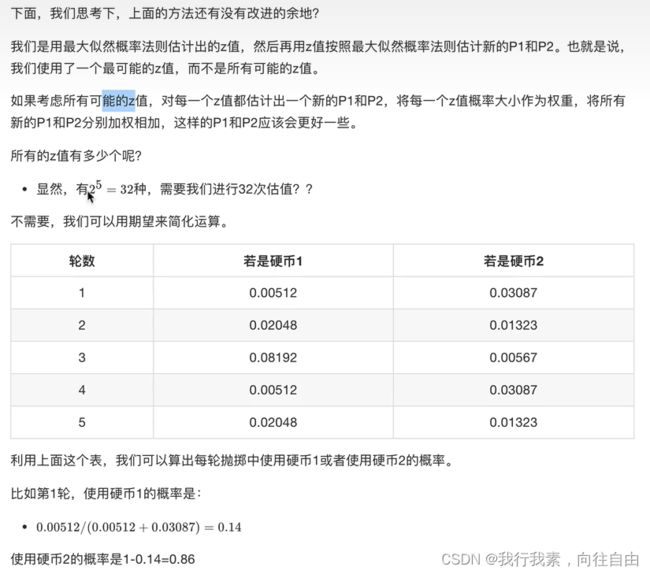
3.3.2 加入隐变量z后的求解
(1)EM初级版
(2)EM进阶版
3.3.3 小结
4.HMM模型
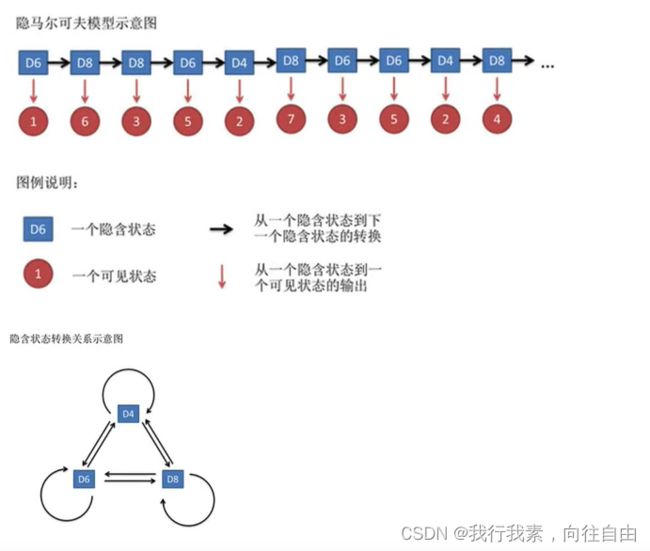
4.1 马尔科夫链
在机器学习算法中,马尔可夫链(Markov chain)是个很重要的概念。马尔可夫链(Markov chain),⼜称离散时间马尔可夫链(discrete-time Markov chain),因俄国数学家安德烈·⻢尔可夫(俄语:Андрей Андреевич Марков)得名。
4.1.1 简介
马尔科夫链即为状态空间中从⼀个状态到另⼀个状态转换的随机过程。无记忆性
4.1.2 经典举例
4.1.3 小结
4.2 HMM简介
隐马尔可夫模型(Hidden Markov Model,HMM)是统计模型,它⽤来描述⼀个含有隐含未知参数的马尔可夫过程。
其难点是从可观察的参数中确定该过程的隐含参数。然后利⽤这些参数来作进⼀步的分析,例如模式识别。
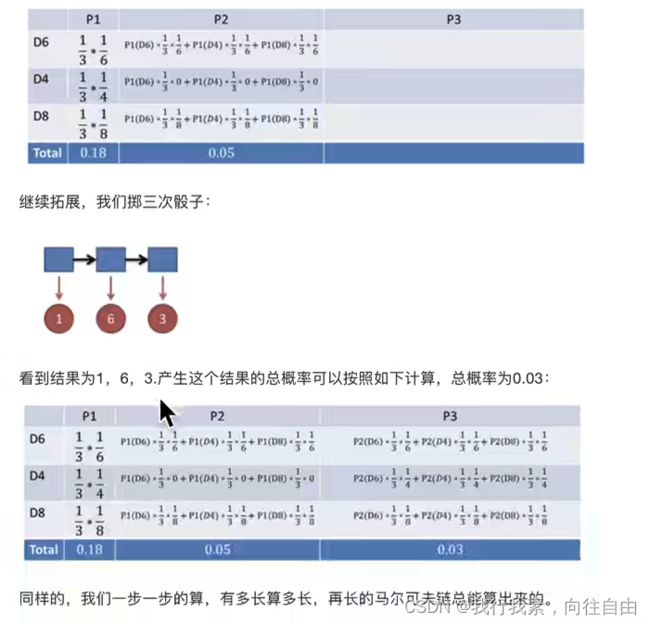
4.2.1 简单案例
4.2.2 案例进阶
(1)问题描述
(2)问题解决
1.一个简单问题【对应问题二】
2.看见不可见的,破解骰子序列【对应问题1】
3.谁动了我的骰子?【对应问题3】
4.2.3 小结
4.3 HMM模型基础
4.3.1 什么样的问题需要HMM模型
4.3.2 HMM模型的定义
![]()
4.3.3 一个HMM模型实例
4.3.4 HMM观测序列的生成
4.3.5 HMM模型的三个基本问题
4.3.6 小结
4.4 前向后向算法评估观察序列概率
4.4.1 回顾HMM问题一:求观测序列的概率
前向后向算法就是来帮助我们在较低的时间复杂度情况下求解这个问题的。
4.4.2 用前向算法求HMM观测序列的概率
前向后向算法是前向算法和后向算法的统称,这两个算法都可以用来求HMM观测序列的概率。我们先来看看前向算法是如何求解这个问题的。
(1)流程梳理
(2)算法总结
4.4.3 HMM前向算法求解实例
![]()
4.4.4 用后向算法求HMM观测序列的概率【了解】
(1)流程梳理
熟悉了⽤前向算法求HMM观测序列的概率,现在我们再来看看怎么⽤后向算法求HMM观测序列的概率。
后向算法和前向算法⾮常类似,都是⽤的动态规划,唯⼀的区别是选择的局部状态不同,后向算法⽤的是“后向概率”。
(2)后向算法流程
4.4.5 小结
4.5 维特比算法解码隐藏状态序列
4.5.1 HMM最可能隐藏状态序列求解概述
4.5.2 维特比算法概述
4.5.3 维特比算法流程总结
4.5.4 维特比算法求解实例
4.6 鲍姆-韦尔奇算法简介
4.6.1 鲍姆-⻙尔奇算法原理
4.7 HMM模型API介绍
4.7.1 API的安装
官⽹链接:hmmlearn — hmmlearn 0.2.7.post20+g37f39b1 documentation
https://hmmlearn.readthedocs.io/en/latest/
pip3 install hmmlearn
4.7.2 hmmlearn的介绍
4.7.3 MultinomialHMM实例
下⾯我们⽤我们在前⾯讲的关于球的那个例⼦使⽤MultinomialHMM跑⼀遍。
import numpy as np
from hmmlearn import hmm
# 设定隐藏状态的集合
states = ["box 1", "box 2", "box3"]
n_states = len(states)
# 设定观察状态的集合
observations = ["red", "white"]
n_observations = len(observations)
# 设定初始状态分布
start_probability = np.array([0.2, 0.4, 0.4])
# 设定状态转移概率分布矩阵
transition_probability = np.array([
[0.5, 0.2, 0.3],
[0.3, 0.5, 0.2],
[0.2, 0.3, 0.5]
])
# 设定观测状态概率矩阵
emission_probability = np.array([
[0.5, 0.5],
[0.4, 0.6],
[0.7, 0.3]
])
# 设定模型参数
model = hmm.MultinomialHMM(n_components=n_states)
model.startprob_=start_probability # 初始状态分布
model.transmat_=transition_probability # 状态转移概率分布矩阵
model.emissionprob_=emission_probability # 观测状态概率矩阵
现在我们来跑⼀跑HMM问题三维特⽐算法的解码过程,使⽤和之前⼀样的观测序列来解码,代码如下:
seen = np.array([[0,1,0]]).T # 设定观测序列
box = model.predict(seen)
print("球的观测顺序为:\n", ", ".join(map(lambda x: observations[x], seen.flatten())))
# 注意:需要使⽤flatten⽅法,把seen从⼆维变成⼀维
print("最可能的隐藏状态序列为:\n", ", ".join(map(lambda x: states[x], box)))
我们再来看看求HMM问题⼀的观测序列的概率的问题,代码如下:
print(model.score(seen)) # 输出结果是:-2.03854530992要注意的是score函数返回的是以⾃然对数为底的对数概率值,我们在HMM问题⼀中⼿动计算的结果是未取对数的原始 概率是0.13022。对⽐⼀下:
import math
math.exp(-2.038545309915233)
# ln0.13022≈−2.0385
# 输出结果是:0.13021800000000003
5.集成学习进阶——回归、分类
5.1 xgboost算法原理
XGBoost(Extreme Gradient Boosting)全名叫极端梯度提升树,XGBoost是集成学习⽅法的王牌,在Kaggle数据挖掘 ⽐赛中,⼤部分获胜者⽤了XGBoost。
XGBoost在绝⼤多数的回归和分类问题上表现的⼗分顶尖,本节将较详细的介绍XGBoost的算法原理。
5.1.1 最优模型的构建方法
应⽤:
- 决策树的⽣成和剪枝分别对应了经验⻛险最⼩化和结构⻛险最⼩化,
- XGBoost的决策树⽣成是结构⻛险最⼩化的结果,后续会详细介绍。
5.1.2 XGBoost的目标函数推导
(1)目标函数的确定
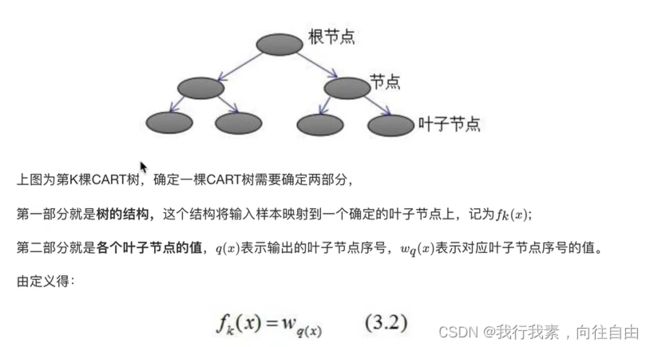
(2)CART树的介绍
(3)树的复杂度定义
1.定义每棵树的复杂度
2.树的复杂度举例
(4)目标函数推导
5.1.3 XGBoost的回归树构建方法
(1)计算分裂节点
(2)停止分裂条件判断
5.1.4 XGBoost与GDBT的区别
5.1.5 小结
5.2 xgboost算法api介绍
5.2.1 xgboost的安装
官⽹链接:
https://xgboost.readthedocs.io/en/latest/pip3 install xgboost
5.2.2 xgboost参数介绍
(1)通用参数
(2)Booster参数
1.Parameters for Tree Booster
2.Parameters for Linear Booster【了解】
(3)学习目标参数
5.3 xgboost案例介绍
5.3.1 案例背景
泰坦尼克号沉没是历史上最臭名昭着的沉船之一。1912年4月15日,在她的处女航中,泰坦尼克号在与冰山相撞后沉没,在2224名乘客和机组人员中造成1502人死亡。这场耸人听闻的悲剧震惊了国际社会,并为船舶制定了更好的安全规定。 造成海难失事的原因之一是乘客和机组人员没有足够的救生艇。尽管幸存下沉有一些运气因素,但有些人比其他人更容易生存,例如妇女,儿童和上流社会。 在这个案例中,我们要求您完成对哪些人可能存活的分析。特别是,我们要求您运用机器学习工具来预测哪些乘客幸免于悲剧。
案例:
https://www.kaggle.com/c/titanic/overview
我们提取到的数据集中的特征包括票的类别,是否存活,乘坐班次,年龄,登陆home.dest,房间,船和性别等。
这是一个常用的数据,给大家个链接,可以去该链接下载数据集:http://biostat.mc.vanderbilt.edu/wiki/pub/Main/DataSets/titanic.txt
上面数据下载可能需要外网访问,本地访问连接超时。
第二种下载数据集方式:
https://datahub.csail.mit.edu/download/jander/historic/file/titanic.csv
经过观察数据得到:
- 1 乘坐班是指乘客班(1,2,3),是社会经济阶层的代表。
- 2 其中age数据存在缺失。
5.3.2 步骤分析
- 1.获取数据
- 2.数据基本处理
- 2.1 确定特征值,目标值
- 2.2 缺失值处理
- 2.3 数据集划分
- 3.特征工程(字典特征抽取)
- 4.机器学习(决策树)
- 5.模型评估
5.3.3 代码实现
- 导入需要的模块
import pandas as pd
import numpy as np
from sklearn.feature_extraction import DictVectorizer
from sklearn.model_selection import train_test_split
from sklearn.tree import DecisionTreeClassifier, export_graphviz
- 1.获取数据
# 1、获取数据
titan=pd.read_csv(r"https://datahub.csail.mit.edu/download/jander/historic/file/titanic.csv")
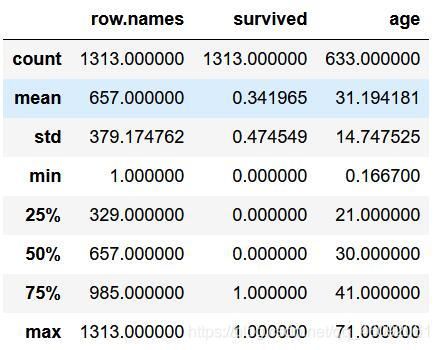
titan.describe()
-
2.数据基本处理
- 2.1 确定特征值,目标值
x = titan[["pclass", "age", "sex"]]
y = titan["survived"]
![]()
- 2.2 缺失值处理
# 缺失值需要处理,将特征当中有类别的这些特征进行字典特征抽取
x['age'].fillna(x['age'].mean(), inplace=True)
- 2.3 数据集划分
x_train, x_test, y_train, y_test = train_test_split(x, y, random_state=22)
- 3.特征工程(字典特征抽取)
特征中出现类别符号,需要进行
one-hot编码处理(DictVectorizer)
x.to_dict(orient="records")需要将数组特征转换成字典数据
# 对于x转换成字典数据x.to_dict(orient="records")
# [{"pclass": "1st", "age": 29.00, "sex": "female"}, {}]
transfer = DictVectorizer(sparse=False)
x_train = transfer.fit_transform(x_train.to_dict(orient="records"))
x_test = transfer.fit_transform(x_test.to_dict(orient="records"))
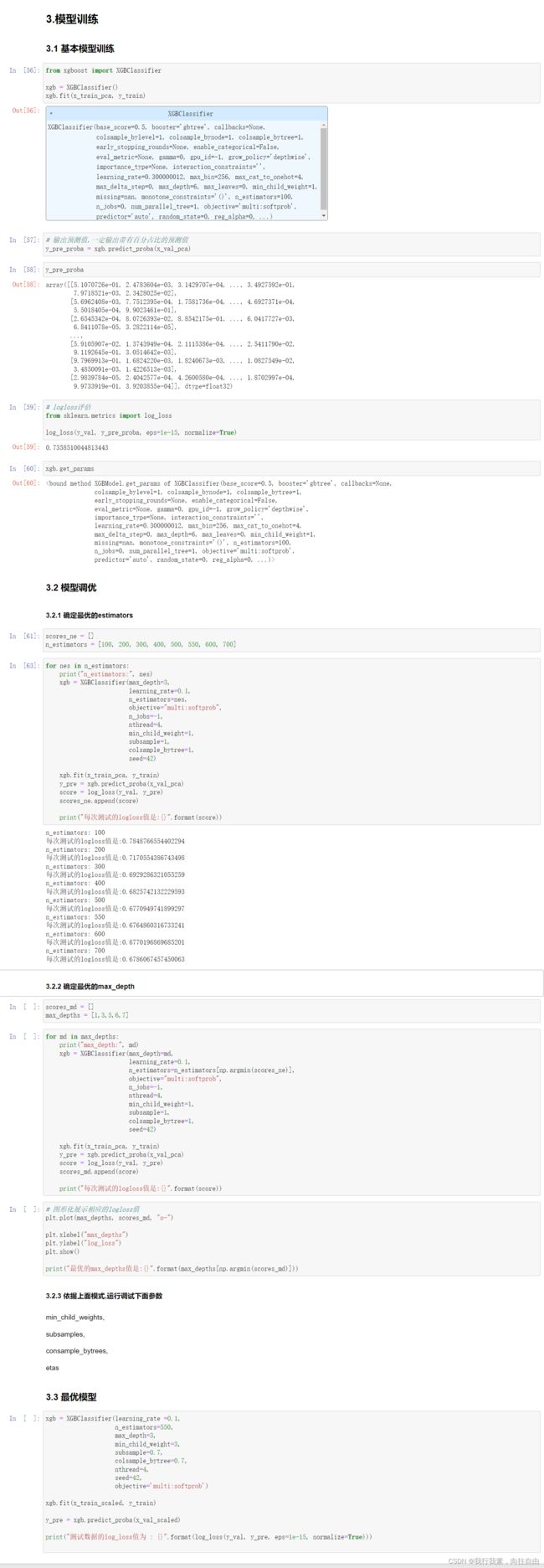
- 4.xgboost模型训练和模型评估
# 模型初步训练
from xgboost import XGBClassifier
xg = XGBClassifier()
xg.fit(x_train, y_train)
xg.score(x_test, y_test)
# 针对max_depth进⾏模型调优
depth_range = range(10)
score = []
for i in depth_range:
xg = XGBClassifier(eta=1, gamma=0, max_depth=i)
xg.fit(x_train, y_train)
s = xg.score(x_test, y_test)
print(s)
score.append(s)
# 结果可视化
import matplotlib.pyplot as plt
plt.plot(depth_range, score)
plt.show()
import numpy as np
import pandas as pd
from sklearn.feature_extraction import DictVectorizer
from sklearn.model_selection import train_test_split
from sklearn.tree import DecisionTreeClassifier,export_graphviz
#1.获取数据
titan = pd.read_csv(r"https://datahub.csail.mit.edu/download/jander/historic/file/titanic.csv")
#2.数据基本处理
#2.1 确定特征值、目标值
x=titan[['pclass','age','sex']]
y=titan['survived']
#2.2 缺失值处理:将特征当中有类别的这些特征进行字典特征抽取
x['age'].fillna(x['age'].mean(),inplace=True)
#2.3 数据集划分
x_train, x_test, y_train, y_test = train_test_split(x, y, random_state=22)
#3.特征工程(字典特征抽取)
# 对于x转换成字典数据x.to_dict(orient="records")
# [{"pclass": "1st", "age": 29.00, "sex": "female"}, {}]
transfer=DictVectorizer(sparse=False)
x_train=transfer.fit_transform(x_train.to_dict(orient='records'))
x_test=transfer.fit_transform(x_test.to_dict(orient='records'))
#4.xgboost模型训练和模型评估
#4.1 模型初步训练
from xgboost import XGBClassifier
xg=XGBClassifier()
xg.fit(x_train,y_train)
xg.score(x_test,y_test)
#4.2 xgboost模型训练和模型评估
depth_range=range(10)
score=[]
for i in depth_range:
xg=XGBClassifier(eta=1,gamma=0,max_depth=i)
xg.fit(x_train,y_train)
s=xg,score(x_test,y_test)
print(s)
score.append(s)
#4.3 结果可视化
import matplotlib.pyplot as plt
plt.plot(depth_range, score)
plt.show()
5.4 otto案例介绍 – Otto Group Product Classification Challenge【xgboost实现】
5.4.1 背景介绍
奥托集团是世界上最⼤的电⼦商务公司之⼀,在20多个国家设有⼦公司。该公司每天都在世界各地销售数百万种产品, 所以对其产品根据性能合理的分类⾮常重要。
不过,在实际⼯作中,⼯作⼈员发现,许多相同的产品得到了不同的分类。本案例要求,你对奥拓集团的产品进⾏正确的分分 类。尽可能的提供分类的准确性。
链接:
https://www.kaggle.com/c/otto-group-product-classification-challenge/overview
5.4.2 思路分析
5.4.3 代码实现
5.5 lightGBM
5.5.1 写在介绍lightGBM之前
(1)lightGBM演进过程
(2)AdaBoost算法
(3)GBDT算法以及优缺点
(4)启发
5.5.2 什么是lightGBM
lightGBM是2017年1⽉,微软在GItHub上开源的⼀个新的梯度提升框架。
Github链接:mirrors / microsoft / LightGBM · GitCode
在开源之后,就被别⼈冠以“速度惊⼈”、“⽀持分布式”、“代码清晰易懂”、“占用内存小”等属性。
LightGBM主打的高效并行训练让其性能超越现有其他boosting工具。在Higgs数据集上的试验表明,LightGBM比 XGBoost快将近10倍,内存占⽤率⼤约为XGBoost的1/6。
higgs数据集介绍:这是⼀个分类问题,⽤于区分产⽣希格斯玻⾊⼦的信号过程和不产⽣希格斯玻⾊⼦的信号过程。
数据链接:UCI Machine Learning Repository: HIGGS Data Set
5.5.3 lightGBM原理
lightGBM 主要基于以下方面优化,提升整体特特性:
- 基于Histogram(直⽅图)的决策树算法
- Lightgbm 的Histogram(直⽅图)做差加速
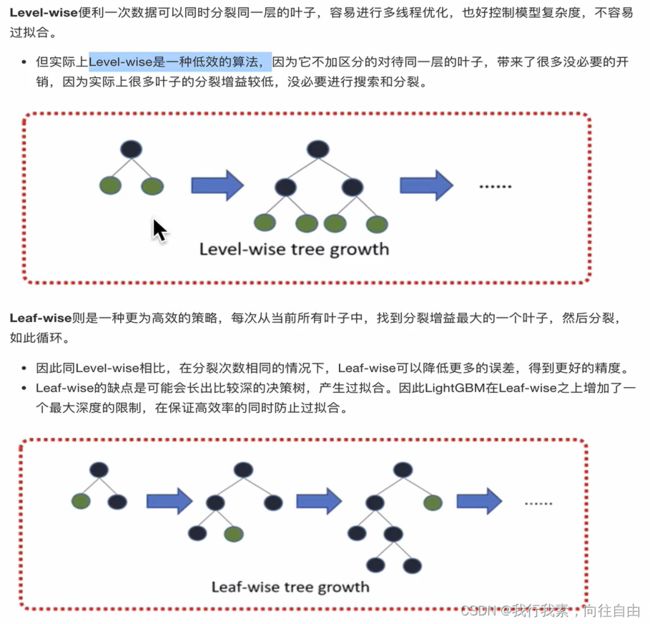
- 带深度限制的Leaf-wise的叶⼦生长策略
- 直接⽀持类别特征
- 直接⽀持高效并行
具体解释见下,分节介绍。
(1)基于Histogram(直⽅图)的决策树算法
直方图算法的基本思想是:
- 先把连续的浮点特征值离散化成k个整数,同时构造⼀个宽度为k的直方图。
- 在遍历数据的时候,根据离散化后的值作为索引在直方图中累积统计量,当遍历⼀次数据后,直⽅图累积了需要的统计量,然后根据直⽅图的离散值,遍历寻找最优的分割点。
Eg:
[0, 0.1) --> 0;
[0.1,0.3) --> 1;
…
(2)Lightgbm 的Histogram(直⽅图)做差加速
(3)带深度限制的Leaf-wise的叶子生长策略
(4)直接支持类别特征
Expo数据集介绍:数据包含1987年10⽉⾄2008年4⽉美国境内所有商业航班的航班到达和离开的详细信息。这是 ⼀个庞⼤的数据集:总共有近1.2亿条记录。主要⽤于预测航班是否准时。
数据链接:2009 - Joint Statistical Computing and Statistical Graphics Section (amstat.org)
(5)直接支持高效并行
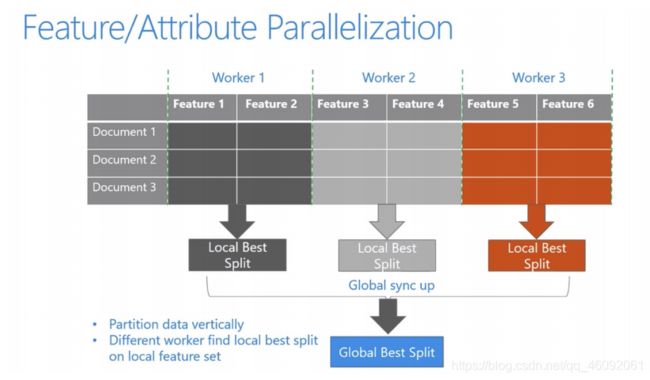
LightGBM还具有支持高效并行的优点。LightGBM原生支持并行学习,目前支持特征并行和数据并行的两种。
- 特征并行的主要思想是在不同机器在不同的特征集合上分别寻找最优的分割点,然后在机器间同步最优的分割点。
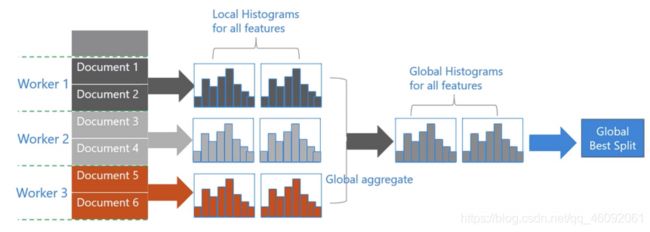
- 数据并行则是让不同的机器先在本地构造直方图,然后进行全局的合并,最后在合并的直⽅图上⾯寻找最优分割点。
LightGBM针对这两种并行方法都做了优化:
5.5.4 小结
5.6 lightGBM算法api介绍
5.6.1 lightGBM的安装
- windows下:
pip install lightgbm- mac下:
链接:LightGBM/Installation-Guide.rst at master · microsoft/LightGBM · GitHub
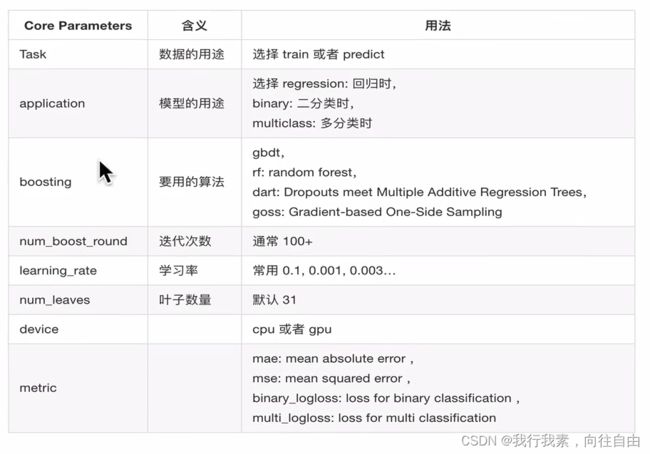
5.6.2 lightGBM参数介绍
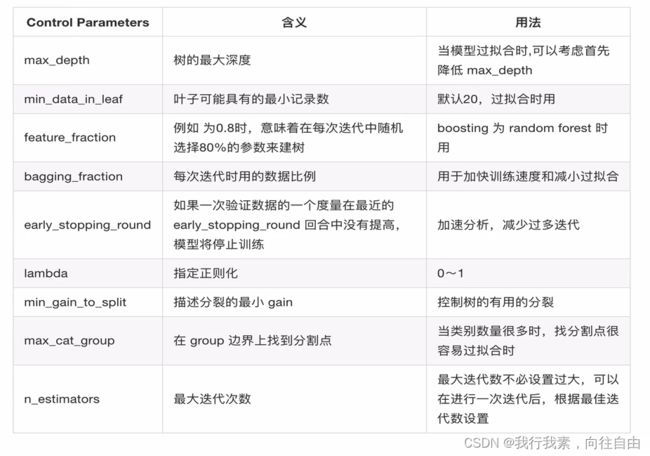
(1)Control Parameters
(3)IO Parameters
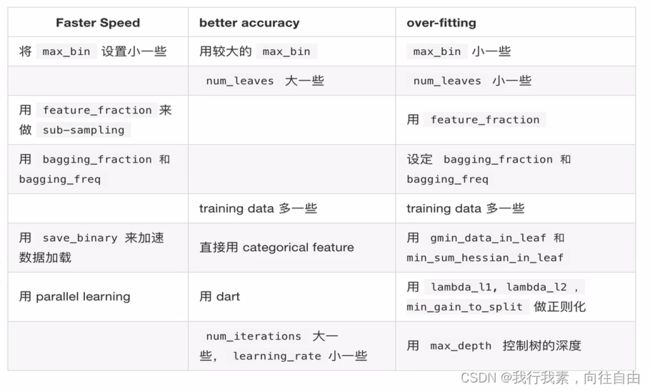
5.6.3 调参建议
下表对应了 Faster Speed ,better accuracy ,over-fitting 三种目的时,可以调的参数
5.7 lightGBM案例介绍
接下来,通过鸢尾花数据集对lightGBM的基本使⽤,做⼀个介绍。
from sklearn.datasets import load_iris
from sklearn.model_selection import train_test_split
from sklearn.model_selection import GridSearchCV
from sklearn.metrics import mean_squared_error
import lightgbm as lgb#加载数据
iris=load_iris()
data=iris.data
target=iris.target
X_train,X_test,y_train,y_test=train_test_split(data,target,test_size=0.2)#模型训练
gbm=lgb.LGBMRegressor(objective='regression',learning_rate=0.05,n_estimators=20)
gbm.fit(X_train,y_train,eval_set=[(X_test,y_test)],eval_metric='l1',early_stopping_rounds=5)
gbm.score(X_test,y_test)#0.8048020597489822#网格搜索,参数优化
estimators=lgb.LGBMRegressor(num_leaves=31)
param_grid = {
'learning_rate': [0.01, 0.1, 1],
'n_estimators': [20, 40, 60, 80]
}
gbm=GridSearchCV(estimators,param_grid,cv=5)
gbm.fit(X_train,y_train)#模型调优训练
gbm=lgb.LGBMRegressor(objective='regression',learning_rate=0.1,n_estimators=20)
gbm.fit(X_train,y_train,eval_set=[(X_test,y_test)],eval_metric='l1', early_stopping_rounds=3)
gbm.score(X_test, y_test)#0.88868853908362035.8 《绝地求生》玩家排名预测
《绝地求生》玩家排名预测_我行我素,向往自由的博客-CSDN博客
6.拓展知识
6.1 向量与矩阵的范数
6.1.1 向量的范数
6.1.2 矩阵的范数
6.2 朗格朗日乘子法
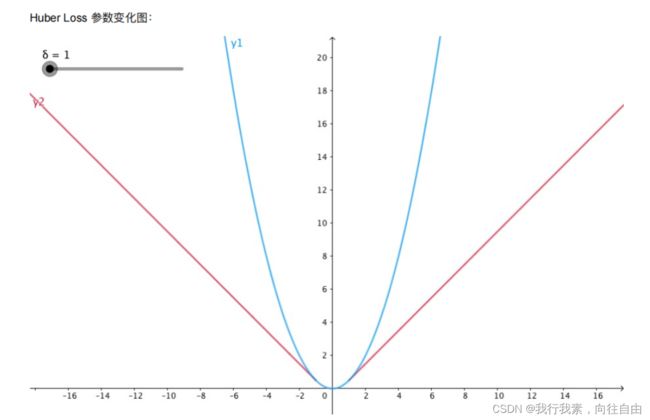
6.3 huber损失函数
6.4 极大似然函数取对数的原因
6.4.1 减少计算量
6.4.2 利于结果更好的计算
但其实可能更重要的一点是,因为概率值都在[0,1]之间,因此,概率的连乘将会变成一个很小的值,可能会引起浮点数下溢,尤其是当数据集很大的时候,联合概率会趋向于0,非常不利于之后的计算。