时间序列模式识别
· 1. Introduction· 2. Exploratory Data Analysis ∘ 2.1 Pattern Changes ∘ 2.2 Correlation Between Features· 3. Anomaly Detection and Pattern Recognition ∘ 3.1 Point Anomaly Detection (System Fault) ∘ 3.2 Collective Anomaly Detection (External Event) ∘ 3.3 Clustering and Pattern Recognition (External Event)· 4. Conclusion·
· 1.简介 · 2.探索性数据分析 ∘2.1 模式更改 ∘2.2 特征之间的相关性 · 3.异常检测和模式识别 ∘3.1 点异常检测(系统故障) ∘3.2 集体异常检测(外部事件) ∘3.3 聚类和模式认可(外部事件) · 4.结论 ·
Note: The detailed project report and the datasets used in this post can be found in my GitHub Page.
注意 :本文中使用的详细项目报告和数据集可以在我的GitHub Page中找到。
1.简介 (1. Introduction)
This project was assigned to me by a client. There is no non-disclosure agreement required and the project does not contain any sensitive information. So, I decide to make this project public as part of my personal data science portfolio while anonymizing the client’s information.
该项目是由客户分配给我的。 不需要保密协议,该项目不包含任何敏感信息。 因此,我决定将该项目公开,作为我的个人数据科学投资组合的一部分,同时匿名化客户的信息。
In the project, there are two data sets, each consists of one week of sensor readings are provided to accomplish the following four tasks:
在该项目中,有两个数据集,每个数据集包含一个星期的传感器读数,以完成以下四个任务:
1. Find anomalies in the data set to automatically flag events
1.在数据集中查找异常以自动标记事件
2. Categorize anomalies as “System fault” or “external event”
2.将异常分类为“系统故障”或“外部事件”
3. Provide any other useful conclusions from the pattern in the data set
3.根据数据集中的模式提供其他有用的结论
4. Visualize inter-dependencies of the features in the dataset
4.可视化数据集中要素的相互依赖性
In this report I am going to briefly walk through the steps I use for data analysis, visualization of feature correlation, machine learning techniques to automatically flag “system faults” and “external events” and my findings from the data.
在本报告中,我将简要介绍我用于数据分析,特征关联可视化,机器学习技术以自动标记“系统故障”和“外部事件”以及我从数据中发现的步骤。
2.探索性数据分析 (2. Exploratory Data Analysis)
My code and results in this section can be found here.
我在本节中的代码和结果可以在这里找到。
The dataset comes with two CSV files, both of which can be accessed from my GitHub Page. I first import and concatenate them into one Pandas dataframe in Python. Some rearrangements are made to remove columns except the 11 features that we are interested in:
该数据集带有两个CSV文件,都可以从我的GitHub Page中访问它们。 我首先将它们导入并用Python连接到一个Pandas数据框中。 除我们感兴趣的11个功能外,还进行了一些重新排列以删除列:
- Ozone 臭氧
- Hydrogen Sulfide 硫化氢
- Total VOCs 总VOC
- Carbon Dioxide 二氧化碳
- PM 1 1号纸
- PM 2.5 下午2.5
- PM 10 下午10点
- Temperature (Internal & External) 温度(内部和外部)
- Humidity (Internal & External). 湿度(内部和外部)。
The timestamps span from May 26 to June 9, 2020 (14 whole days in total) in EDT (GMT-4) time zone. By subtraction, different intervals are found between each reading, ranging from 7 seconds to 3552 seconds. The top 5 frequent time intervals are listed below in Table 1, where most of them are close to 59 and 60 seconds, so it can be concluded that the sensor reads every minute. However, the inconsistency of reading intervals might be worth looking into if it is no deliberate interference involved since it might cause trouble in future time series analysis.
时间戳跨越EDT(GMT-4)时区的2020年5月26日至6月9日(共14天)。 通过减法,可以在每个读数之间找到不同的间隔,范围从7秒到3552秒。 下面的表1中列出了前5个最频繁的时间间隔,其中大多数时间间隔接近59秒和60秒,因此可以得出结论,传感器每分钟都会读取一次。 但是,如果不涉及故意的干扰,则可能需要研究读取间隔的不一致,因为这可能会在以后的时间序列分析中造成麻烦。
For each of the features, the time series data are on different scales, so they are normalized in order for better visualization and machine learning efficiencies. Then they are plotted and visually inspected to discover any interesting patterns.
对于每个功能,时间序列数据的比例不同,因此对其进行了归一化,以实现更好的可视化和机器学习效率。 然后将它们绘制出来并进行视觉检查,以发现任何有趣的图案。
2.1模式变更 (2.1 Pattern Changes)
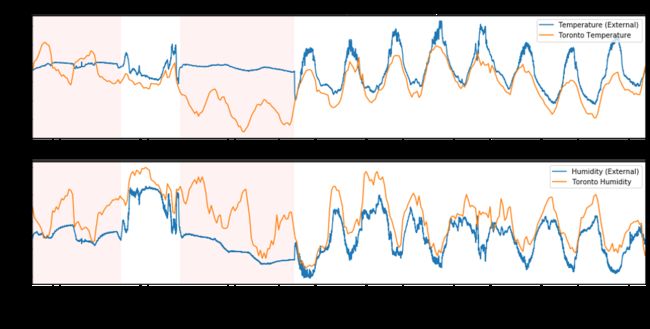
Some of the features seem to share similar pattern changes at specific time points. Three of the most significant ones (Temperature External, Humidity External, and Ozone) are shown below in Figure 1. It can be clearly seen that the areas highlighted with pink tend to have flat signals while the unhighlighted areas are sinusoidal.
一些功能似乎在特定时间点共享相似的模式更改。 图1中显示了三个最重要的区域(外部温度,外部湿度和臭氧)。可以清楚地看到,用粉红色突出显示的区域倾向于发出平坦的信号,而未突出显示的区域则是正弦的。
According to common sense, the outdoor temperature reaches its high point at noon and goes down at night, I start to wonder the possibility that different test environments were involved during this 14-day period. To test the idea, Toronto weather data is queried from Canada Weather Stats [1]. The temperature and relative humidity are overlaid and compared with the external temperature and humidity in this dataset. The plot is shown in Figure 2. It can be seen that the actual temperature and humidity fluctuate in a sinusoidal fashion. Most parts of the temperature and humidity readings correlate well with the weather data, while the areas highlighted in pink remains relatively invariant. I am not provided with any relevant information on the environments that the measurements were taken, but from the plot, it can be reasonably inferred that the device has been relocated between indoor and outdoor environments during the 14-day period. This is also tested later in the automatic anomaly detection in Section 3.3.
根据常识,室外温度会在中午达到最高点,并在晚上下降,我开始怀疑在这14天的时间内是否涉及不同的测试环境。 为了验证这个想法,可以从加拿大天气统计中查询多伦多的天气数据[1]。 覆盖温度和相对湿度,并与该数据集中的外部温度和湿度进行比较。 该图如图2所示。可以看出,实际温度和湿度以正弦形式波动。 温度和湿度读数的大部分与天气数据具有良好的相关性,而用粉红色突出显示的区域则相对不变。 在进行测量的环境中,我没有得到任何相关信息,但是从绘图中可以合理地推断出该设备在14天的时间内已在室内和室外环境之间重新放置。 稍后还将在3.3节中的自动异常检测中对此进行测试。
Figure 2: Temperature (External) and Humidity (External) overlaid with Toronto weather data. The pink highlighted areas remain relatively invariant compared to others. 图2:用多伦多天气数据覆盖的温度(外部)和湿度(外部)。 与其他区域相比,粉红色突出显示的区域保持相对不变。2.2特征之间的关联 (2.2 Correlation Between Features)
Correlation is a technique for investigating the relationship between two quantitative, continuous variables in order to represent their inter-dependencies. Among different correlation techniques, Pearson’s correlation is the most common one, which measures the strength of association between the two variables. Its correlation coefficient scales from -1 to 1, where 1 represents the strongest positive correlation, -1 represents the strongest negative correlation and 0 represents no correlation. The correlation coefficients between each pair of the dataset are calculated and plotted as a heatmap, shown in Table 2. The scatter matrix of selected features is also plotted and attached in the Appendix section.
关联是一种技术,用于研究两个定量的连续变量之间的关系,以表示它们之间的相互依赖性。 在不同的相关技术中,Pearson相关是最常见的一种,它测量两个变量之间的关联强度。 其相关系数从-1到1,其中1表示最强的正相关,-1表示最强的负相关,0表示无相关。 计算每对数据集之间的相关系数,并将其绘制为热图,如表2所示。选定要素的散布矩阵也被绘制并附在附录部分。
The first thing to be noticed is that PM 1, PM 2.5, and PM 10 are highly correlated with each other, which means they always fluctuate in the same fashion. Ozone is negatively correlated with Carbon Dioxide and positively correlates with Temperature (Internal) and Temperature (External). On the other hand, it is surprising not to find any significant correlation between Temperature (Internal) and Temperature (External), possibly due to the superior thermal insulation of the instrument. However, since there is no relevant knowledge provided, no conclusions can be made on the reasonability of this finding. Except for Ozone, Temperature (Internal) is also negatively correlated with Carbon Dioxide, Hydrogen Sulfide, and the three particulate matter measures. On the contrary, Temperature (External) positively correlates with Humidity (Internal) and three particulate matter measures, while negatively correlates with Humidity (External), just as what can be found from the time series plots in Figure 1.
首先要注意的是,PM 1,PM 2.5和PM 10彼此高度相关,这意味着它们始终以相同的方式波动。 臭氧与二氧化碳呈负相关,与温度(内部)和温度(外部)呈正相关。 另一方面,令人惊讶的是,没有发现温度(内部)和温度(外部)之间的任何显着相关性,这可能是由于仪器具有出色的隔热性。 但是,由于没有提供相关的知识,因此无法就此发现的合理性得出任何结论。 除臭氧外,温度(内部)还与二氧化碳,硫化氢和三种颗粒物度量值呈负相关。 相反,温度(外部)与湿度(内部)和三个颗粒物度量呈正相关,而与湿度(外部)呈负相关,正如图1的时间序列图所示。
3.异常检测和模式识别 (3. Anomaly Detection and Pattern Recognition)
In this section, various anomaly detection methods are examined based on the dataset. The data come without labels, so there is no knowledge or classification rule is provided to distinguish between “system faults”, “external events” and others. Any details of the instrument and experiments are not provided either. Therefore, my results in this section might deviate from expectations, but I am trying my best to make assumptions, define problems, and then accomplish them based on my personal experience. The section consists of three parts: Point Anomaly Detection, Collective Anomaly Detection, and Clustering.
在本节中,将基于数据集检查各种异常检测方法。 数据没有标签,因此没有提供知识或分类规则来区分“系统故障”,“外部事件”和其他。 也没有提供仪器和实验的任何细节。 因此,我在本节中的结果可能会偏离预期,但我会尽力做出假设,定义问题,然后根据我的个人经验完成这些假设。 本节包括三个部分:点异常检测,集体异常检测和聚类。
3.1点异常检测(系统故障) (3.1 Point Anomaly Detection (System Fault))
Point anomalies, or global outliers, are those data points that are entirely outside the scope of the usual signals without any support of close neighbors. It is usually caused by human or system error and needs to be removed during data cleaning for better performance in predictive modeling. In this dataset, by assuming the “system faults” are equivalent to such point anomalies, there are several features that are worth examining, such as the examples shown below in Figure 3.
点异常或全局离群值是完全不在常规信号范围内而没有任何近邻支持的数据点。 它通常是由人为或系统错误引起的,需要在数据清理过程中将其删除以在预测建模中获得更好的性能。 在此数据集中,通过假设“系统故障”等效于此类点异常,有几个特性值得研究,例如下面的图3中所示的示例。
Figure 3: Time series signals before (left) and after (right) automatic flagging. The point anomalies (outliers) are marked as red. From top to bottom: Humidity (Internal), Total VOCs, and Carbon Dioxide. 图3:自动标记之前(左)和之后(右)的时间序列信号。 点异常(异常值)标记为红色。 从上至下:湿度(内部),总VOC和二氧化碳。Here, from Humidity (Internal) to Total VOC to Carbon Dioxide, each represents a distinct complexity of point anomaly detection tasks. In the first one, three outliers sit on the level of 0, so a simple boolean filter can do its job of flagging these data points. In the second one, the outliers deviate significantly from the signal that we are interested in, so linear thresholds can be used to separate out the outliers. Both cases are easy to implement because they can be done by purely experience-based methods. When it comes to the third case, it is not possible to use a linear threshold to separate out the outliers since even if they deviate from its neighbors, the values may not be as great as the usual signals at other time points.
在这里,从湿度(内部)到总VOC到二氧化碳,每个都代表了点异常检测任务的独特复杂性。 在第一个中,三个离群值位于0级别上,因此一个简单的布尔过滤器可以完成标记这些数据点的工作。 在第二个中,离群值明显偏离了我们感兴趣的信号,因此可以使用线性阈值来分离离群值。 两种情况都易于实现,因为它们可以通过纯粹基于经验的方法来完成。 在第三种情况下,不可能使用线性阈值来分离离群值,因为即使离群值偏离其邻域,其值也可能不如其他时间点的正常信号大。
For such cases, there are many ways to approach. One of the simple ways is to calculate the rolling mean or median at each time point and test if the actual value is within the prediction interval that is calculated by adding and subtracting a certain fluctuation range from the central line. Since we are dealing with outliers in our case, the rolling median is more robust, so it is used in this dataset.
对于这种情况,有很多方法可以解决。 一种简单的方法是计算每个时间点的滚动平均值或中位数,并测试实际值是否在预测区间内,该预测区间是通过从中心线增加或减去某个波动范围而得出的。 由于在这种情况下我们正在处理离群值,因此滚动中位数更为稳健,因此在此数据集中使用了滚动中位数。
From Figure 4, it is even clearer to demonstrate this approach: Equal-distance prediction intervals are set based on the rolling median. Here, the rolling window is set to 5, which means that for each data point, we take four of its closest neighbors and calculate the median as the center of prediction. Then a prediction interval of ±0.17 is padded around the center. Any points outside are considered as outliers.
从图4中可以更清楚地证明这种方法:等距预测间隔基于滚动中值设置。 在这里,滚动窗口设置为5,这意味着对于每个数据点,我们取其四个最近的邻居并计算中位数作为预测中心。 然后,在中心周围填充±0.17的预测间隔。 外部的任何点均视为异常值。
It is straightforward and efficient to detect the point anomalies using this approach. However, it has deficiencies and may not be reliable enough to deal with more complex data. In this model, there are two parameters: rolling window size and prediction interval size, both of which are defined manually through experimentations with the given data. We are essentially solving the problem encountered when going from case 2 to case 3 as seen in Figure 3 by enabling the self-adjusting capability to the classification boundary between signal and outliers according to time. However, the bandwidth is fixed, so it becomes less useful in cases when the definition of point anomalies changes with time. For example, the definition of a super cheap flight ticket might be totally different between a normal weekday and the holiday season.
使用这种方法来检测点异常非常简单有效。 但是,它有缺陷并且可能不够可靠,无法处理更复杂的数据。 在此模型中,有两个参数:滚动窗口大小和预测间隔大小,这两个参数都是通过对给定数据进行实验来手动定义的。 如图3所示,我们基本上是通过从情况2转到情况3来解决问题,方法是根据时间启用信号和离群值之间的分类边界的自调整功能。 但是,带宽是固定的,因此在点异常的定义随时间变化的情况下,带宽变得不再有用。 例如,在正常工作日和假日季节之间,超廉价机票的定义可能完全不同。
That is when machine learning comes into play, where the model can learn from the data to adjust the parameters by itself when the time changes. It will know when a data point can be classified as point anomaly or not at a specific time point. However, I cannot construct such a supervised machine learning model on this task for this dataset since the premise is to have labeled data, and ours is not. It would be still be suggested to go along this path in the future because with such a model, the most accurate results will be generated no matter how complex the system or the data are.
那就是机器学习开始发挥作用的时候,模型可以从数据中学习,以在时间变化时自行调整参数。 它将知道何时可以在特定时间点将数据点归类为点异常或不将其分类为点异常。 但是,我不能为此数据集在此任务上构造这样的监督机器学习模型,因为前提是要有标记数据,而我们没有。 仍建议在将来沿这条路走,因为使用这种模型,无论系统或数据多么复杂,都将产生最准确的结果。
Even though supervised learning methods would not work in this task, there are unsupervised learning techniques that can be useful such as clustering, also discussed in subsection 3.3. Clustering can group unlabeled data by using similarity measures, such as the distance between data points in the vector space. Then the point anomalies can be distinguished by selecting those far away from cluster centers. However, in order to use clustering for point anomaly detection in this dataset, we have to follow the assumption that external events are defined with the scope of multiple features instead of treating every single time series separately. More details on this are discussed in the following two subsections 3.2 and 3.3.
即使在这种任务下不能使用监督学习方法,也有一些有用的无监督学习技术,例如聚类,也在3.3小节中进行了讨论。 聚类可以使用相似性度量(例如向量空间中数据点之间的距离)对未标记的数据进行分组。 然后可以通过选择远离聚类中心的点来区分点异常。 但是,为了将聚类用于此数据集中的点异常检测,我们必须遵循这样的假设:外部事件是在多个特征的范围内定义的,而不是分别处理每个时间序列。 以下两个小节3.2和3.3讨论了有关此问题的更多详细信息。
3.2集体异常检测(外部事件) (3.2 Collective Anomaly Detection (External Event))
If we define the “system fault” as point anomaly, then there are two directions to go with the “external event”. One of them is to define it as a collective anomaly that appears in every single time-series signals. The idea of collective anomaly is on the contrary to point anomaly. Point anomalies are discontinued values that are greatly deviated from usual signals while collective anomalies are usually continuous, but the values are out of expectations, such as significant increase or decrease at some time points. In this subsection, all 11 features are treated separately as a single time series. Then the task is to find the abrupt changes that happen in each of them.
如果我们将“系统故障”定义为点异常,则“外部事件”有两个方向。 其中之一是将其定义为出现在每个时间序列信号中的集体异常。 集体异常的概念与点异常相反。 点异常是不连续的值,与通常的信号有很大的偏离,而集体异常通常是连续的,但是这些值超出了预期,例如在某些时间点显着增加或减少。 在本小节中,所有11个功能部件均被视为一个时间序列。 然后的任务是找到每个变化都发生的突变。
For such a problem, one typical approach is to tweak the usage of time series forecasting: we can fit a model to a certain time period before and predict the value after. The actual value is then compared to see if it falls into the prediction interval. It is very similar to the rolling median method used in the previous subsection, but only the previous time points are used here instead of using neighbors from both directions.
对于这样的问题,一种典型的方法是调整时间序列预测的用法:我们可以将模型拟合到之前的某个时间段,然后预测之后的值。 然后将实际值进行比较,以查看其是否落在预测间隔内。 它与上一小节中使用的滚动中值方法非常相似,但是此处仅使用前一个时间点,而不是使用双向的邻居。
There are different options for the model as well. Traditional time series forecast models like SARIMA is a good candidate, but the model may not be complex enough to accommodate the “patterns” that I mentioned in Section 2.1 and Section 3.3. Another option is to train a supervised regression model for the time series, which is quite widely used nowadays.
该模型也有不同的选择。 传统的时间序列预测模型(如SARIMA)是不错的选择,但该模型可能不够复杂,无法适应我在2.1节和3.3节中提到的“模式”。 另一种选择是为时间序列训练监督回归模型,该模型在当今已被广泛使用。
The idea is simple: Features are extracted from the time series using the concept of the sliding window, as seen in Table 3 and Figure 5. The sliding window size (blue) is set to be the same as the desired feature number k. Then for each data point (orange) in the time series, the features are data point values from its lag 1 to lag k before. As a result, a time series with N samples is able to be transformed into a table of N-k observations and k features. Next, by implementing the concept of “forward chaining”, each point is predicted by the regression model trained using observations from indices of 0 to k-1. In addition to the main regression model, two more quantile regressors are trained with different significance levels to predict the upper and lower bounds of the prediction interval, with which we are able to tell the actual value is above or below the interval band.
这个想法很简单:使用滑动窗口的概念从时间序列中提取特征,如表3和图5所示。滑动窗口的大小(蓝色)设置为与所需特征编号k相同。 然后,对于时间序列中的每个数据点(橙色),特征都是从滞后1到滞后k的数据点值。 结果,具有N个样本的时间序列可以转换为Nk个观测值和k个特征的表。 接下来,通过实施“正向链接”的概念,通过使用从0到k-1的索引的观察值训练的回归模型来预测每个点。 除了主要的回归模型外,还训练了另外两个具有不同显着性水平的分位数回归器,以预测预测区间的上限和下限,由此我们可以判断出实际值是在区间带之上还是之下。
This method is applied to the given dataset, and an example is shown below as a result in Figure 6. The Ozone time series is hourly sampled for faster training speed and the features are extracted and fed into three Gradient Boosting Regressor models (1 main and 2 quantile regressors) using Scikit-Learn. The significance levels are chosen so that the prediction level represents a 90% confidence interval (shown as green in Figure 6 Top). The actual values are then compared with the prediction interval and flagged with red (unexpected increase) and blue (unexpected decrease) in Figure 6 Bottom.
此方法适用于给定的数据集,结果如图6所示。下面是示例。每小时对臭氧时间序列进行采样,以提高训练速度,并提取特征并将其输入到三个Gradient Boosting Regressor模型(1个主要模型和2个分位数回归)使用Scikit-Learn。 选择显着性水平,以便预测水平代表90%的置信区间(在图6顶部显示为绿色)。 然后,将实际值与预测间隔进行比较,并在图6底部用红色(意外增加)和蓝色(意外减少)标记。
The results may not be super impressive yet, because more work still needs to be done around regression model selections and hyperparameter fine-tunings. However, it is already showing its capability of fagging these abrupt increases and decreases in all these spikes. One great thing about using machine learning models is that the model learns and evolves by itself when feeding with data. From Figure 6 Bottom, it can be seen that the last three hills (after about 240 hours) have fewer flagged points than the previous ones. It is not only because the magnitudes are smaller, but also due to the fact that the model is learning from the previous experience and start to adapt to the “idea” that it is now in “mountains” and periodic fluctuations should be expected. Therefore, it is not hard to conclude that the model performance can get better and better if more data instances are fed.
结果可能不会令人印象深刻,因为围绕回归模型选择和超参数微调仍需要做更多的工作。 但是,它已经显示出阻止所有这些尖峰中这些突然增加和减少的能力。 使用机器学习模型的一大好处是,模型在输入数据时会自行学习和演化。 从图6的底部可以看出,最后三个山丘(约240小时后)的标记点比以前的要少。 这不仅是因为幅度较小,而且还因为该模型是从以前的经验中学到并开始适应“思想”的事实,因此它现在处于“山脉”中,应该预期会出现周期性波动。 因此,不难得出这样的结论:如果馈送了更多的数据实例,则模型性能会越来越好。
Beyond this quantile regression model, deep learning models such as LSTM might be able to achieve better performance. Long Short Term Memory (LSTM) is a specialized artificial Recurrent Neural Network (RNN) that is one of the state-of-the-art choices of sequence modeling due to its special design of feedback connections. However, it takes much longer time and effort to set up and fine-tune the network architecture, which exceeds the time allowance of this project, so it is not included as the presentable content in this report.
除了这种分位数回归模型之外,诸如LSTM之类的深度学习模型也许还能获得更好的性能。 长短期记忆(LSTM)是一种专门的人工循环神经网络(RNN),由于其特殊的反馈连接设计,它是序列建模的最新选择之一。 但是,建立和微调网络体系结构需要花费更多的时间和精力,这超出了该项目的时间限制,因此在本报告中未将其包括在内。
Again, on the other hand, as I mentioned in previous sections, the provided data does not come with labels showing which data points are considered as anomalies. It does cause difficulties in the collective anomaly detection task discussed in this subsection by limiting the model choices and performance. In the future, if some labels are provided, it will become a semi-supervised or supervised learning problem, so that it will become easier to achieve better results.
同样,另一方面,正如我在前面的部分中提到的那样,所提供的数据没有附带标签,这些标签显示哪些数据点被视为异常。 通过限制模型的选择和性能,确实在本小节讨论的集体异常检测任务中造成了困难。 将来,如果提供一些标签,它将成为半监督或有监督的学习问题,以便变得更容易获得更好的结果。
3.3聚类和模式识别(外部事件) (3.3 Clustering and Pattern Recognition (External Event))
As I mentioned in subsection 3.2 above, recognizing the “external events” can be approached in two directions: one is to treat every time series separately and monitor any unexpected changes happened to the sensor signals, and the other one is to assume the events affect multiple features at the same time so that we hope to distinguish the events by looking at the unique characteristics shown in different features. In this case, if we have labeled data, it would be a common classification problem, but even without labels, we are still able to approach by clustering.
正如我在上面的3.2小节中提到的,认识“外部事件”可以从两个方向进行:一个是分别处理每个时间序列并监视传感器信号发生的任何意外变化,另一个是假设事件影响因此,我们希望通过查看不同功能中显示的独特特征来区分事件。 在这种情况下,如果我们为数据加标签,这将是一个常见的分类问题,但是即使没有标签,我们仍然能够通过聚类进行处理。
Clustering is an unsupervised machine learning technique that finds similarities between data according to the characteristics and groups similar data objects into clusters. It can be used as a stand-alone tool to get insights into data distribution and can also be used as a preprocessing step for other algorithms. There are many distinct methods of clustering, and here I am using two of the most commonly used ones: K-Means and DBSCAN.
聚类是一种无监督的机器学习技术,可根据特征查找数据之间的相似性,并将相似的数据对象分组。 它可以用作独立工具来深入了解数据分布,也可以用作其他算法的预处理步骤。 有许多不同的集群方法,这里我使用两种最常用的方法:K-Means和DBSCAN。
K-means is one of the partitioning methods used for clustering. It randomly partitions objects into nonempty subsets and constantly adding new objects and adjust the centroids until a local minimum is met when optimizing the sum of squared distance between each object and centroid. On the other hand, Density-Based Spatial Clustering of Applications with Noise (DBSCAN) is a density-based method where a cluster is defined as the maximal set of density-connected points [3].
K均值是用于聚类的一种分区方法。 它将对象随机划分为非空子集,并不断添加新对象并调整质心,直到优化每个对象与质心之间的平方距离之和达到局部最小值为止。 另一方面,带噪声的基于密度的应用程序空间聚类(DBSCAN)是一种基于密度的方法,其中,将聚类定义为密度连接点的最大集合[3]。
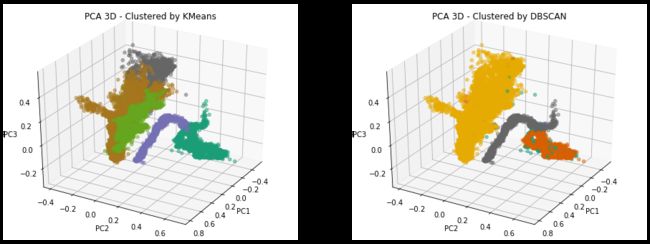
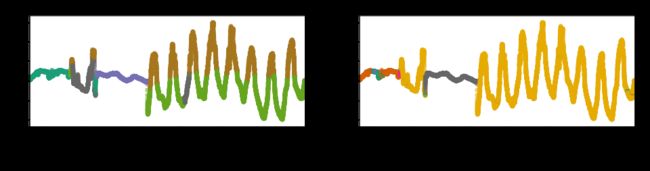
Principal Components Analysis (PCA) is a dimension reduction technique that creates new uncorrelated variables in order to increase interpretability and minimize information loss. In this project, after applying K-means and DBSCAN algorithms on the normalized data, PCA is performed and the clustering results are plotted in both 2D (Figure 7) and 3D (Figure 8) using the first 2 and 3 principal components. In addition, to view the clustering results from another perspective, the labeled time series plots are made, and the Temperature (External) plot is shown in Figure 9 as an example.
主成分分析(PCA)是一种降维技术,可创建新的不相关变量以提高可解释性并最大程度地减少信息丢失。 在这个项目中,在对标准化数据应用K-means和DBSCAN算法之后,执行PCA,并使用前2个和3个主成分在2D(图7)和3D(图8)中绘制聚类结果。 此外,要从另一个角度查看聚类结果,请绘制标记的时间序列图,并以温度(外部)图为例,如图9所示。
From the plots, it can be clearly seen that both methods are able to distinguish between the indoor/outdoor pattern changes that I mentioned in section 2.1. The main difference is that the partition-based K-means method is more sensitive to the magnitude changes caused by day/night alternation. Many variables in the dataset are subject to such obvious sinusoidal changes that happen at the same time, including Temperature (External and Internal), Humidity (External and internal) and Ozone. K-means tend to treat peaks and valleys differently. On the other hand, density-based DBSCAN cares less about the magnitude difference but pays more attention to the density distributions. Therefore, it clusters the whole sinusoidal part as one mass cloud as seen in Figure 7 and Figure 8.
从图中可以清楚地看到,两种方法都能够区分我在2.1节中提到的室内/室外模式变化。 主要区别在于基于分区的K均值方法对昼夜交替引起的幅度变化更敏感。 数据集中的许多变量会同时发生明显的正弦变化,包括温度(外部和内部),湿度(外部和内部)和臭氧。 K均值倾向于以不同的方式对待峰谷。 另一方面,基于密度的DBSCAN不太关心幅度差异,而更多地关注密度分布。 因此,它将整个正弦曲线部分聚集为一个质量云,如图7和图8所示。
It is not possible to comment on which clustering method is better than the other at this stage because they are distinctive enough to function for different interests. If we are more interested in treating the high-low portions of the sinusoidal signals differently, we are going to use K-means; if we only want to distinguish between indoor/outdoor mode, then DBSCAN is better. In addition, since it is an unsupervised learning task, there is no way of quantifying the performance between models except for visualizing and judging by experience. In the future, if some labeled data is provided, the results can be turned into a semi-supervised learning task, and more intuitions can be gained toward model selection.
在此阶段,无法评论哪种聚类方法比另一种更好,因为它们具有足够的独特性,可以针对不同的利益发挥作用。 如果我们对以不同的方式处理正弦信号的高-低部分更感兴趣,我们将使用K-means。 如果我们只想区分室内/室外模式,则DBSCAN更好。 此外,由于这是一项无监督的学习任务,因此除了根据经验进行可视化和判断外,无法量化模型之间的性能。 将来,如果提供一些标记的数据,则可以将结果转换为半监督学习任务,并且可以获得更多的直觉来进行模型选择。
4。结论 (4. Conclusion)
In this post, I briefly walk through the approaches and findings of exploratory data analysis and correlation analysis, as well as the constructions of three distinct modeling pipelines that used for point anomaly detection, collective anomaly detection, and clustering.
在本文中,我简要介绍了探索性数据分析和相关性分析的方法和发现,以及用于点异常检测,集体异常检测和聚类的三个不同的建模管道的构建。
In the exploratory data analysis section, the sensor reading time intervals are found to vary severely. Even if most of them are contained around a minute, the inconsistency problem is still worth looking into due to the fact that it might lower the efficiency and performance of analytical tasks. The measuring environment is found subject to changes from the time series plots and later reassured by aligning with the actual Toronto weather data as well as the clustering results. In addition, the correlation between features is studied and exemplified. A few confusions are raised such as the strange relationship between Temperature (Internal) and Temperature (External), which needs to be studied through experiments or the device itself.
在探索性数据分析部分中,发现传感器读取时间间隔变化很大。 即使其中大多数都在大约一分钟之内,但由于不一致的问题可能会降低分析任务的效率和性能,因此仍然值得研究。 发现测量环境可能会随着时间序列图的变化而变化,随后通过与实际的多伦多天气数据以及聚类结果保持一致来放心。 另外,研究并举例说明了特征之间的相关性。 引起了一些混乱,例如温度(内部)和温度(外部)之间的奇怪关系,需要通过实验或设备本身进行研究。
In the anomaly detection section, since “system fault” and “external event” are not clearly defined, I split the project into three different tasks. Point anomalies are defined as severely deviated and discontinued data points. The rolling median method is used here to successfully automate the process of labeling such point anomalies. Collective anomalies, on the other hand, are defined as the deviated collection of data points, usually seen as abrupt increases or decreases. This task is accomplished by extracting features from time series data and then training of regression models. Clustering is also performed on the dataset using K-mean and DBSCAN, both of which play to their strength and successfully clustered data by leveraging their similar and dissimilar characteristics.
在异常检测部分,由于未明确定义“系统故障”和“外部事件”,因此我将项目分为三个不同的任务。 点异常定义为严重偏离和中断的数据点。 这里使用滚动中值法来成功地自动标记此类点异常的过程。 另一方面,集体异常定义为偏离的数据点集合,通常被视为突然增加或减少。 通过从时间序列数据中提取特征,然后训练回归模型来完成此任务。 还使用K均值和DBSCAN对数据集执行聚类,两者均发挥了自己的优势,并通过利用它们的相似和不同特性成功地对数据进行了聚类。
All of the anomaly detection models introduced in this project are only prototypes without extensive model sections and fine-tunings. There are great potentials for each of them to evolve into better forms if putting more effort and through gaining more knowledge of the data. For point anomalies, there are many more machine-learning-based outlier detection techniques such as isolation forest and local outlier factors to accommodate for more complex data forms. For collective anomaly, state-of-the-art LSTM is worth putting effort into, especially in time series data and sequence modeling. For clustering, there are many other families of methods, such as hierarchical and grid-based clustering. They are capable of achieving similar great performance.
本项目中介绍的所有异常检测模型只是原型,没有广泛的模型部分和微调。 如果付出更多的努力并获得更多的数据知识,他们每个人都有很大的潜力发展成更好的形式。 对于点异常,还有更多基于机器学习的离群值检测技术,例如隔离林和局部离群值因素,可以适应更复杂的数据形式。 对于集体异常,值得投入最新的LSTM,特别是在时间序列数据和序列建模方面。 对于群集,还有许多其他方法系列,例如分层和基于网格的群集。 它们能够实现类似的出色性能。
Of course, these future directions are advised based on the premise of no labeled data. If experienced engineers or scientists are able to give their insights on which types of data are considered as “system fault” or “external event”, more exciting progress will surely be made by transforming the tasks into semi-supervised or supervised learning problems, where more tools will be available to choose.
当然,这些未来的方向是在没有标签数据的前提下提出的。 如果经验丰富的工程师或科学家能够就哪些数据类型被视为“系统故障”或“外部事件”给出自己的见解,那么将任务转变为半监督或监督学习问题肯定会取得更加令人兴奋的进展。有更多工具可供选择。
翻译自: https://towardsdatascience.com/time-series-pattern-recognition-with-air-quality-sensor-data-4b94710bb290
时间序列模式识别