离散小波变换DWT-小波变换和脑电信号特征提取（Matlab代码实现）

           目录

1 概述

2 运行结果

3 参考文献

‍4 Matlab代码

---

1 概述

小波变换是从20世纪80年代起逐渐发展成熟的一项数学应用技术，具有对时间—频率的双重分析和多分辨率分析能力，目前已经广泛应用于图像处理、模式识别等多个领域。小波变换的窗口大小固定但形状可改变，因此能够满足时域—频域局部化分析要求。离散小波变换比连续小波变换的去噪效果更好，更适用于实际应用。

小波变换首先通过分解信号，使信号的能量集中在一些大的小波系数中，而噪声的能量分布于整个小波域内；然后通过阈值降噪，选择合适的阈值将有用信号的系数保留，将噪声信号的系数置零，从而去除噪声；最后再对经过阈值降噪后的系数进行重构，得到去除噪声后的信号。

常用的小波基函数有Meyer小波、Coiflet(coif N）小波、Daubechies(db N）小波等。为得到较好的去噪效果，所选取的小波基函数在对心电信号进行分解时，应尽量保留心电信号中的有用分量，同时使噪声分解对应的小波系数差异尽可能大。Coiflet4小波基与心电信号的波形最为相似，同时与输出信号具有良好的相关性，重构后的信号信噪比大、均方误差小，因此本文选用Coiflet4小波基进行小波分解。

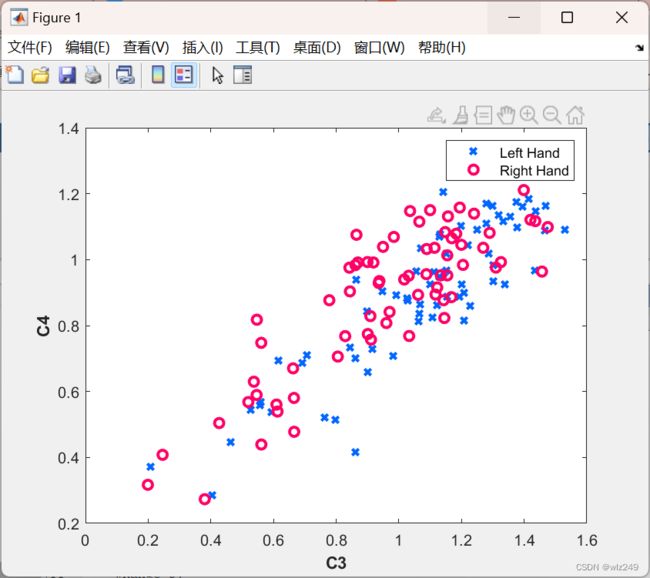
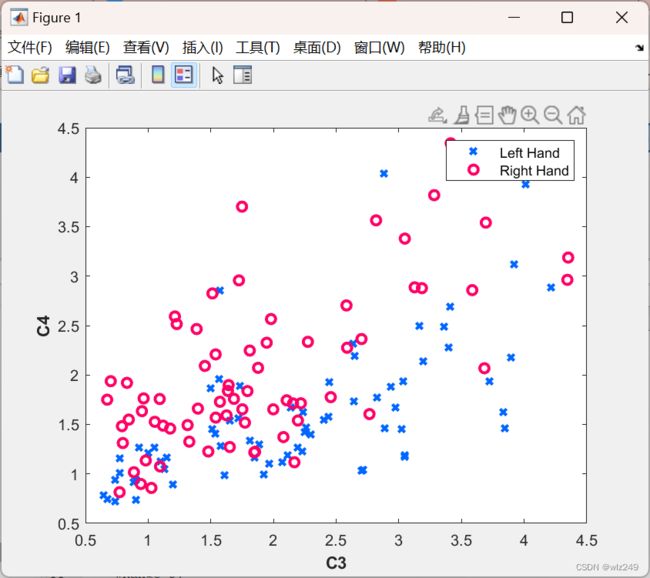
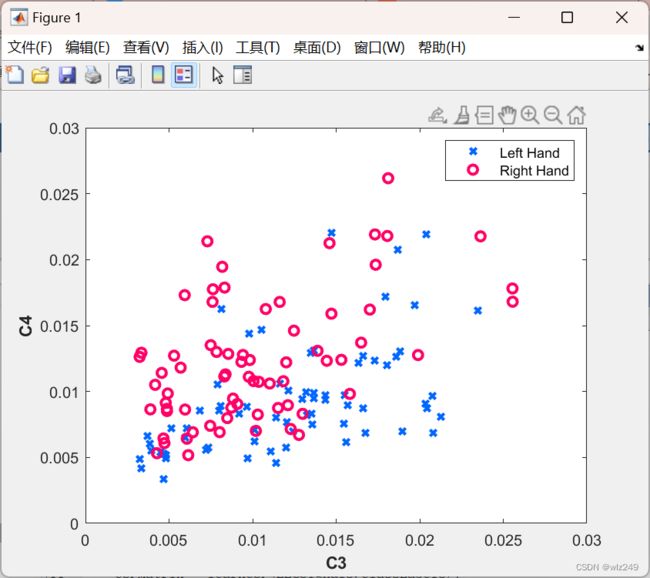
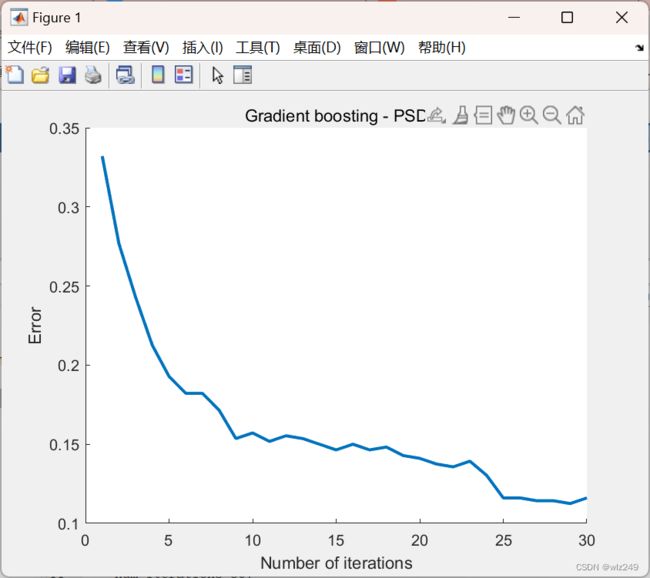
2 运行结果

 

 

 

 

 

 

 

3 参考文献

[1]赵薇. 基于图卷积的运动想象脑电信号分类技术研究[D].河北师范大学,2022.DOI:10.27110/d.cnki.ghsfu.2022.000058.

‍4 Matlab代码

主函数部分代码：

% Extract Discrete Wavelet Transform (DWT) Feature
close all; clear; clc;

load dataset_BCIcomp1.mat
Y=y_train;

% Range is 0 to 9 sec
startS=0;
endS=9;
wStep=1;
wRange=9;

X=extractDWT(x_train,startS,endS,wStep,wRange);
T=extractDWT(x_test,startS,endS,wStep,wRange);
save dataDWT.mat X Y T

color_L = [0 102 255] ./ 255;
color_R = [255, 0, 102] ./ 255;

pos = find(Y==1);
plot(X(pos,1),X(pos,2),'x','Color',color_L,'LineWidth',2);

hold on
pos = find(Y==2);
plot(X(pos,1),X(pos,2),'o','Color',color_R,'LineWidth',2);

legend('Left Hand','Right Hand')
xlabel('C3','fontweight','bold')
ylabel('C4','fontweight','bold')