读书笔记：无人机控制（六）

基于预测控制的多架小型直升机编队飞行控制

本部分将介绍多架小型无人直升机编队飞行控制，作为 UAV 高级控制的一个示例。自主编队飞行控制系统设计为“领导者–跟随”模型。为了在系统约束下获得良好的控制性能，将“模型预测控制”应用于随动直升机的平动位置控制。在实时最优控制计算中，考虑了运动范围和避碰等位置约束。为了实现对干扰的鲁棒性，使用最小阶干扰观测器来估计不可测量的状态变量和干扰。

编队控制

以鸟类和鱼类为灵感的编队控制是多交通工具系统中的热门话题。在无人机的自主飞行控制中，除了稳定性外，还需要高控制性能。具体可参考机器人编队控制。

在本部分中。首先将直升机动力学建模为线性状态空间方程。其次，利用模型预测控制（MPC）设计了每个跟随器的位置控制器。成本函数以具有终端状态成本的线性二次型形式表示。此外，它还被扩充为一种反映避碰机动和通信范围的形式。

Leader–Follower 系统

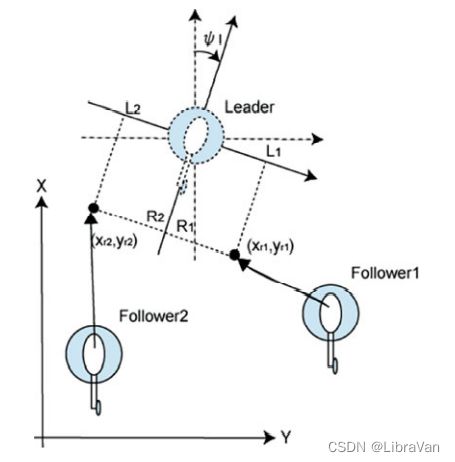
此处由于考虑的是直升机，因而 leader 和 follower 之间的追踪可视为一个二维追踪，即 $$\left[\begin{array}{c}{X}_{rp}\\ Y_{rp}\end{array}\right]=\left[\begin{array}{c}{X}_l+R_p\cos {\psi }_l-L_p\sin {\psi }_l\\ Y_l+R_p\sin {\psi }_l+L_p\cos {\psi }_l\end{array}\right],p=1,2,\cdots ,n.$$

• $X_{rp}/Y_{rp}$ 是 follower 在惯性系中的参考轨迹；
• $X_l/Y_l$ 是 leader 在惯性系中的参考轨迹；
• $R_p/L_p$ 是 follower $p$ 相对于 leader 的位置坐标系的偏移量；
• ${\psi }_l$ 是 leader 的方向角。
  

基于模型预测控制的控制器设计

本部分介绍一种分层制导控制器的设计方法，该控制器可使每个跟随者跟踪到指定的参考目标和编队结构。

速度控制模型

首先介绍一个基于修正速度模型 $$\begin{array}{r}{G}_{vx}=-g\frac{b}{s+b}\frac{1}{s-a},\\ G_{vy}=g\frac{b}{s+b}\frac{1}{s-a},\end{array}$$ 的平移速度和位置模型。

具体而言，现考虑的坐标体系如下图所示。但由于直升机的平动与垂直运动可以独立考虑，在仅考虑平动时，坐标轴取 $X^{\prime }O{Y}^{\prime }$。

平动模型

假设其平动速率上界为 $5$ m/s，记 $x_v^{\prime }=[{\dot{X}}^{\prime }{\ddot{X}}^{\prime }{\dot{Y}}^{\prime }{\ddot{Y}}^{\prime }{]}^{\mathrm{T}}$，$u^{\prime }(t)=[\theta (t)\varphi (t){]}^{\mathrm{T}}$，其平动模型为 $$\begin{array}{rl}{\dot{x}}_v^{\prime }& =A_v{x}_x(t)+B_v{u}^{\prime }(t),\\ y^{\prime }(t)& =C_v{x}_v^{\prime }(t).\end{array}$$ 其中，$$A_v=\left[\begin{array}{cccc}0& 1& 0& 0\\ aT& a-T& 0& 0\\ 0& 0& 0& 1\\ 0& 0& aT& a-T\end{array}\right],B_v=\left[\begin{array}{cc}0& 0\\ -gT& 0\\ 0& 0\\ 0& gT\end{array}\right],C_v=\left[\begin{array}{cccc}1& 0& 0& 0\\ 0& 0& 1& 0\end{array}\right],$$ 且 $T=2.00$，$a=0.20$，$g$ 是重力常数。

• 由于速度的测量是在惯性系下进行的，因而需要坐标变换 $$\left[\begin{array}{c}\dot{X}\\ \dot{Y}\end{array}\right]=\left[\begin{array}{cc}\cos \psi & -\sin \psi \\ \sin \psi & \cos \psi \end{array}\right]\left[\begin{array}{c}{\dot{X}}^{\prime }\\ {\dot{Y}}^{\prime }\end{array}\right],$$ $$\left[\begin{array}{c}{u}_X\\ u_Y\end{array}\right]=\left[\begin{array}{cc}\cos \psi & -\sin \psi \\ \sin \psi & \cos \psi \end{array}\right]\left[\begin{array}{c}\theta \\ \varphi \end{array}\right].$$ 进而得到系统模型为 $$\begin{array}{rl}& {\dot{x}}_{vp\mathrm{a}\mathrm{r}\mathrm{g}\mathrm{u}\mathrm{m}\mathrm{e}\mathrm{n}\mathrm{t}}(t)=A_v{x}_{vp}(t)+B_v{u}_{vp}+G_v{r}_{vp},\\ & A_v=\left[\begin{array}{cc}{A}_v& 0_{4\times 2}\\ -C_v& 0_{2\times 2}\end{array}\right],B_v=\left[\begin{array}{cc}{B}_v& \\ 0_{2\times 2}& \end{array}\right],G_v=\left[\begin{array}{c}{0}_{4\times 2}\\ I_2\end{array}\right],\\ & x_{vp\mathrm{a}\mathrm{r}\mathrm{g}\mathrm{u}\mathrm{m}\mathrm{e}\mathrm{n}\mathrm{t}}={\left[\begin{array}{cc}{x}_{vp}^{\mathrm{T}}(t)& {\epsilon }_{vp}^{\mathrm{T}}(t)\end{array}\right]}^{\mathrm{T}}.\end{array}$$
• 基于上述模型，将性能指标降至最低的反馈控制输入为 $$\begin{array}{rl}{J}_{vp}& ={\int }_0^{\infty }{x}_{vp}^{\mathrm{T}}(\tau )Q_v{x}_{vp\mathrm{a}\mathrm{r}\mathrm{g}\mathrm{u}\mathrm{m}\mathrm{e}\mathrm{n}\mathrm{t}}(\tau )+u_{vp}^{\mathrm{T}}(\tau )R_v{u}_{vp}(\tau )d\tau ,\\ Q_v& \ge 0,R_v>0.\end{array}$$
• 进一步地，速度闭环系统为 $${\dot{x}}_{vp\mathrm{a}\mathrm{r}\mathrm{g}\mathrm{u}\mathrm{m}\mathrm{e}\mathrm{n}\mathrm{t}}=(A_v-B_v{F}_v)x_{vp}(t)+G_v{r}_{vp}(t).$$ 则平移位置模型为 $$\begin{array}{r}{\dot{x}}_p=A{x}_p(t)+B{r}_{vp}(t)\\ y_p(t)=C{x}_p(t).\end{array}$$ 其中，$$A=\left[\begin{array}{cccccccc}0& 0& 1& 0& 0& 0& 0& 0\\ 0& 0& 0& 0& 1& 0& 0& 0\\ 0_{6\times 1}& & A_v& -& B_v& F_v& & \end{array}\right],$$ $$B=\left[\begin{array}{c}{0}_{2\times 2}\\ G_v\end{array}\right],C=\left[\begin{array}{cc}{I}_2& 0_{2\times 6}\end{array}\right],x_p(t)={\left[\begin{array}{ccc}{X}_p(t)& Y_p(t)& x_{vp\mathrm{a}\mathrm{r}\mathrm{g}\mathrm{u}\mathrm{m}\mathrm{e}\mathrm{n}\mathrm{t}}^{\mathrm{T}}\end{array}\right]}^{\mathrm{T}}.$$

模型预测控制器设计

利用 MPC (Model Predictive Controller) 方法推导了制导控制器。在 MPC 设计中，以二次形式描述性能指标，并考虑到系统的约束，如碰撞避免和通信范围。

模型预测控制

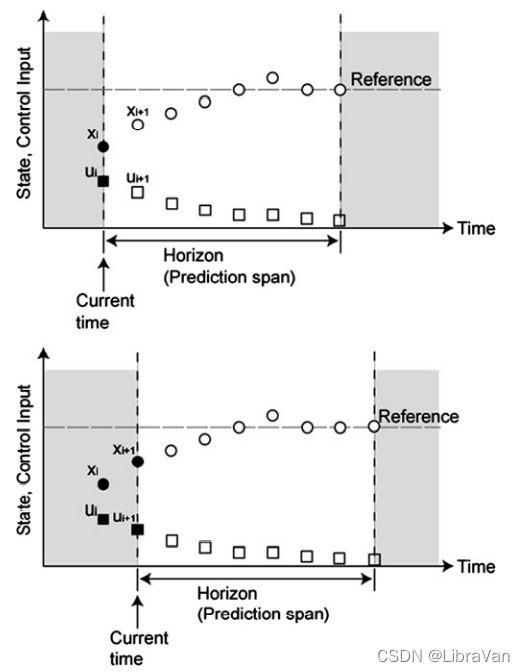
模型预测控制是一种基于模型的控制方法，它在每次考虑系统的轨迹跟踪或约束后，优化从当前时间到未来有限时间的响应。最优控制的范围随着时间的推移而减小，因此，这种方法也被称为后退范围控制。相关可参见模型预测控制介绍。

控制器设计

为了在没有任何跟踪误差的情况下跟踪参考位置设计了伺服系统。扩充状态方程如下 $$\begin{array}{rl}{\dot{x}}_p& =A{x}_p(t)+B{r}_{vp}(t)+G{r}_p(t),\\ A& =\left[\begin{array}{cc}A& 0_{8\times 2}\\ -C& 0_{2\times 2}\end{array}\right],B=\left[\begin{array}{c}B\\ 0_{2\times 2}\end{array}\right],G=\left[\begin{array}{c}{0}_{8\times 2}\\ I_2\end{array}\right],\\ x_p& ={\left[\begin{array}{cc}{x}_p^{\mathrm{T}}& {\epsilon }_p^{\mathrm{T}}\end{array}\right]}^{\mathrm{T}}.\end{array}$$

接下来在多架直升机的飞行中设置约束，即通信约束和碰撞约束。

• 通信约束。当通过改变 $(R_p,L_p)$ 来改变队形时。考虑到每架直升机的通信距离，即 $X_{\min }\le X_p-X_l\le X_{\max }$，$Y_{\min }\le Y_p-Y_l\le Y_{\max }$，设置以下约束条件以限制第 $p$ 个 follower 的位置，$$\begin{array}{rl}{g}_1(x_{\mathrm{g}\mathrm{a}\mathrm{p}})& =X_{\min }-(X_p-X_l)\le 0,\\ g_2(x_{\mathrm{g}\mathrm{a}\mathrm{p}})& =(X_p-X_l)-X_{\max }\le 0,\\ g_3(x_{\mathrm{g}\mathrm{a}\mathrm{p}})& =Y_{\min }-(Y_p-Y_l)\le 0,\\ g_4(x_{\mathrm{g}\mathrm{a}\mathrm{p}})& =(Y_p-Y_l)-Y_{\max }\le 0.\end{array}$$
• 进而设置的惩罚函数为 $$P_j=\{\begin{array}{l}{\left[g_j{x}_p-\frac{{\mu }_k}{2}{h}_k(t)\right]}^2+3{\left(\frac{{\mu }_k{h}_h(t)}{2}\right)}^2,g_j(x_a)>0,\\ \frac{({\mu }_k{h}_k(t){)}^3}{g_j(x_p)+{\mu }_k{h}_k(t)},g_j(x_a)\le 0.\end{array}$$ 此处 ${\mu }_k>{\mu }_{k+1}>0$，${\lim }_{k\to \infty }{\mu }_k=0$，$h_k(t)\ge 0$。当 $g_j<0$，$h_k(t)=0$是最优轨迹。
• 碰撞约束。在第 $p$ 个飞行器处增加人工势函数 $$\begin{array}{rl}{P}_c& =L\ln \left[a_p^2(X_p-X_q{)}^2+b_p^2(Y_p-Y_q{)}^2\right],\\ K& =\{\begin{array}{ll}{K}_o,& \sqrt{(X_p-X_q{)}^2+(Y_p-Y_q{)}^2}<d,\\ 0,& \sqrt{(X_p-X_q{)}^2+(Y_p-Y_q{)}^2}\ge d.\end{array}\end{array}$$
  此处，$K_o$，$a_p$，$b_p$ 均为调整性能的参数。

在此约束基础上，进而得到最优实时控制。