机器学习之XGBoost算法
机器学习之XGBoost算法
1. 什么是XGBoost
XGBoost是陈天奇等人开发的一个开源机器学习项目,高效地实现了GBDT算法并进行了算法和工程上的许多改进,被广泛应用在Kaggle竞赛及其他许多机器学习竞赛中并取得了不错的成绩。
说到XGBoost,不得不提GBDT(Gradient Boosting Decision Tree)。因为XGBoost本质上还是一个GBDT,但是力争把速度和效率发挥到极致,所以叫X (Extreme) GBoosted。包括前面说过,两者都是boosting方法。
关于GBDT,这里不再提,可以查看我下一篇的介绍。
1.1 XGBoost树的定义
先来举个例子,我们要预测一家人对电子游戏的喜好程度,考虑到年轻和年老相比,年轻更可能喜欢电子游戏,以及男性和女性相比,男性更喜欢电子游戏,故先根据年龄大小区分小孩和大人,然后再通过性别区分开是男是女,逐一给各人在电子游戏喜好程度上打分,如下图所示。
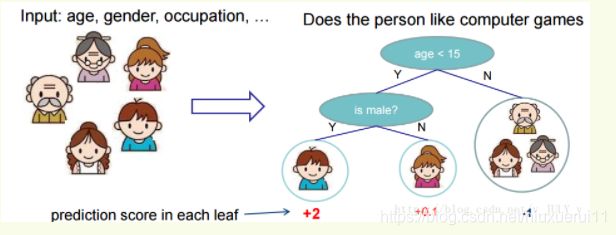
就这样,训练出了2棵树tree1和tree2,类似之前gbdt的原理,两棵树的结论累加起来便是最终的结论,所以小孩的预测分数就是两棵树中小孩所落到的结点的分数相加:2 + 0.9 = 2.9。爷爷的预测分数同理:-1 + (-0.9)= -1.9。具体如下图所示:
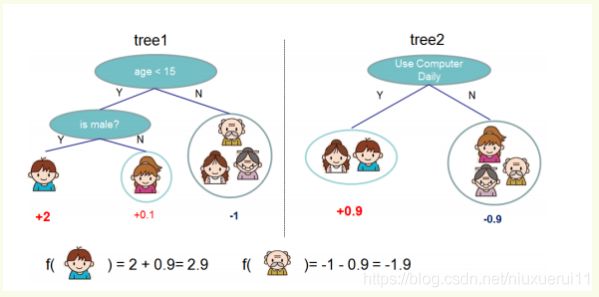
恩,你可能要拍案而起了,惊呼,这不是跟上文介绍的GBDT乃异曲同工么?
事实上,如果不考虑工程实现、解决问题上的一些差异,XGBoost与GBDT比较大的不同就是目标函数的定义。XGBoost的目标函数如下图所示:

其中:
红色箭头所指向的L 即为损失函数(比如平方损失函数:l(yi,yi)=(yi−yi)2)
红色方框所框起来的是正则项(包括L1正则、L2正则) 红色圆圈所圈起来的为常数项
对于f(x),XGBoost利用泰勒展开三项,做一个近似。f(x)表示的是其中一颗回归树。
XGBoost的核心算法思想不难,基本就是:
1、不断地添加树,不断地进行特征分裂来生长一棵树,每次添加一个树,其实是学习一个新函数f(x),去拟合上次预测的残差。
2、当我们训练完成得到k棵树,我们要预测一个样本的分数,其实就是根据这个样本的特征,在每棵树中会落到对应的一个叶子节点,每个叶子节点就对应一个分数
3、最后只需要将每棵树对应的分数加起来就是该样本的预测值。
显然,我们的目标是要使得树群的预测值y′i尽量接近真实值yi,而且有尽量大的泛化能力。类似之前GBDT的套路,XGBoost也是需要将多棵树的得分累加得到最终的预测得分(每一次迭代,都在现有树的基础上,增加一棵树去拟合前面树的预测结果与真实值之间的残差)。

那接下来,我们如何选择每一轮加入什么 f 呢?答案是非常直接的,选取一个 f 来使得我们的目标函数尽量最大地降低。这里 f 可以使用泰勒展开公式近似。

实质是把样本分配到叶子结点会对应一个obj,优化过程就是obj优化。也就是分裂节点到叶子不同的组合,不同的组合对应不同obj,所有的优化围绕这个思想展开。到目前为止我们讨论了目标函数中的第一个部分:训练误差。接下来我们讨论目标函数的第二个部分:正则项,即如何定义树的复杂度。
1.2 正则项:树的复杂度
XGBoost对树的复杂度包含了两个部分:
1、一个是树里面叶子节点的个数T
2、一个是树上叶子节点的得分w的L2模平方(对w进行L2正则化,相当于针对每个叶结点的得分增加L2平滑,目的是为了避免过拟合)
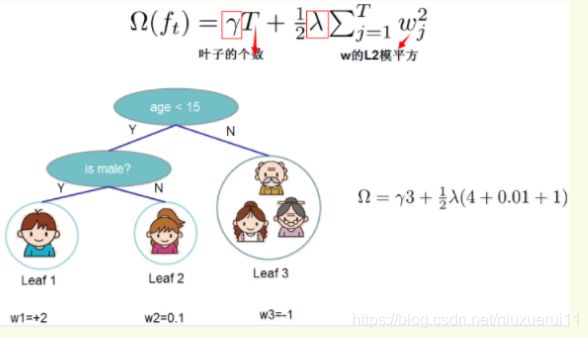
我们再来看一下XGBoost的目标函数(损失函数揭示训练误差 + 正则化定义复杂度):
L(ϕ)=∑il(y′i−yi)+∑kΩ(ft)
正则化公式也就是目标函数的后半部分,对于上式而言,y′i是整个累加模型的输出,正则化项∑kΩ(ft)是则表示树的复杂度的函数,值越小复杂度越低,泛化能力越强。
1.3 树该怎么长
很有意思的一个事是,我们从头到尾了解了xgboost如何优化、如何计算,但树到底长啥样,我们却一直没看到。很显然,一棵树的生成是由一个节点一分为二,然后不断分裂最终形成为整棵树。那么树怎么分裂的就成为了接下来我们要探讨的关键。对于一个叶子节点如何进行分裂,XGBoost作者在其原始论文中给出了一种分裂节点的方法:枚举所有不同树结构的贪心法
不断地枚举不同树的结构,然后利用打分函数来寻找出一个最优结构的树,接着加入到模型中,不断重复这样的操作。这个寻找的过程使用的就是贪心算法。选择一个feature分裂,计算loss function最小值,然后再选一个feature分裂,又得到一个loss function最小值,你枚举完,找一个效果最好的,把树给分裂,就得到了小树苗。
总而言之,XGBoost使用了和CART回归树一样的想法,利用贪婪算法,遍历所有特征的所有特征划分点,不同的是使用的目标函数不一样。具体做法就是分裂后的目标函数值比单子叶子节点的目标函数的增益,同时为了限制树生长过深,还加了个阈值,只有当增益大于该阈值才进行分裂。从而继续分裂,形成一棵树,再形成一棵树,每次在上一次的预测基础上取最优进一步分裂/建树。
1.4 如何停止树的循环生成
凡是这种循环迭代的方式必定有停止条件,什么时候停止呢?简言之,设置树的最大深度、当样本权重和小于设定阈值时停止生长以防止过拟合。具体而言,则
1、当引入的分裂带来的增益小于设定阀值的时候,我们可以忽略掉这个分裂,所以并不是每一次分裂loss
function整体都会增加的,有点预剪枝的意思,阈值参数为(即正则项里叶子节点数T的系数);
2、当树达到最大深度时则停止建立决策树,设置一个超参数max_depth,避免树太深导致学习局部样本,从而过拟合;
3、样本权重和小于设定阈值时则停止建树。什么意思呢,即涉及到一个超参数-最小的样本权重和min_child_weight,和GBM的
min_child_leaf 参数类似,但不完全一样。大意就是一个叶子节点样本太少了,也终止同样是防止过拟合;
2. XGBoost与GBDT有什么不同
除了算法上与传统的GBDT有一些不同外,XGBoost还在工程实现上做了大量的优化。总的来说,两者之间的区别和联系可以总结成以下几个方面。
1、GBDT是机器学习算法,XGBoost是该算法的工程实现。 2、在使用CART作为基分类器时,XGBoost显式地加入了正则项来控制模
型的复杂度,有利于防止过拟合,从而提高模型的泛化能力。 3、GBDT在模型训练时只使用了代价函数的一阶导数信息,XGBoost对代
价函数进行二阶泰勒展开,可以同时使用一阶和二阶导数。 4、传统的GBDT采用CART作为基分类器,XGBoost支持多种类型的基分类
器,比如线性分类器。 5、传统的GBDT在每轮迭代时使用全部的数据,XGBoost则采用了与随机 森林相似的策略,支持对数据进行采样。
6、传统的GBDT没有设计对缺失值进行处理,XGBoost能够自动学习出缺 失值的处理策略。
3. 为什么XGBoost要用泰勒展开,优势在哪里?
XGBoost使用了一阶和二阶偏导, 二阶导数有利于梯度下降的更快更准. 使用泰勒展开取得函数做自变量的二阶导数形式, 可以在不选定损失函数具体形式的情况下, 仅仅依靠输入数据的值就可以进行叶子分裂优化计算, 本质上也就把损失函数的选取和模型算法优化/参数选择分开了. 这种去耦合增加了XGBoost的适用性, 使得它按需选取损失函数, 可以用于分类, 也可以用于回归。
4. 代码实现
import xgboost
# First XGBoost model for Pima Indians dataset
from numpy import loadtxt
from xgboost import XGBClassifier
from sklearn.model_selection import train_test_split
from sklearn.metrics import accuracy_score
# load data
dataset = loadtxt('pima-indians-diabetes.csv', delimiter=",")
# split data into X and y
X = dataset[:,0:8]
Y = dataset[:,8]
# split data into train and test sets
seed = 7
test_size = 0.33
X_train, X_test, y_train, y_test = train_test_split(X, Y, test_size=test_size, random_state=seed)
# fit model no training data
model = XGBClassifier()
model.fit(X_train, y_train)
# make predictions for test data
y_pred = model.predict(X_test)
predictions = [round(value) for value in y_pred]
# evaluate predictions
accuracy = accuracy_score(y_test, predictions)
print("Accuracy: %.2f%%" % (accuracy * 100.0))
Accuracy: 77.95%