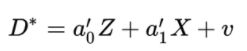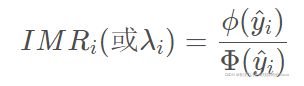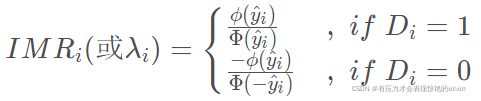Heckman两阶段模型学习笔记

有近两周的时间都在学习Heckman两阶段模型。网上看了一些资料，在CSDN里找到了几篇珍贵的学习笔记，有一篇相当于带我入了门学习笔记 | Heckman两阶段法介绍_Claire_chen_jia的博客-CSDN博客_heckman两阶段，

另一篇内容非常详细，也非常丰富，OSABEr的博客_CSDN博客-DID,双重差分法,计量经济学领域Heckman两步法 | 样本选择模型 & 处理效应模型_KEMOSABEr的博客-CSDN博客_样本选择模型，OSABEr的博客_CSDN博客-DID,双重差分法,计量经济学领域，可见作者之用心。花了好几天才看完，不过是在看了前一篇博文的基础上才基本看懂了。

此外，在某些理解点上，选择性偏差（selection bias）指的是什么？ - 知乎和Heckman模型学习笔记_猜火车98的博客-CSDN博客_heckman模型 也起到了非常的点化作用。

至此对Heckman模型有了基本认识，也做一下简单的学习笔记，针对其中难懂的地方会加入自己的一些解释与举例。这份笔记许多地方也借鉴了这些博文，感谢博主们的分享！

目录

1.Heckman模型的由来

2.选择偏差、样本选择偏差、自选择偏差与遗漏变量误差

3.样本选择模型与处理效应模型

a.Heckman两阶段模型/样本选择模

b.处理效应模型

4.模型的Stata实现

a.样本选择模型代码（针对样本选择偏差）

b.处理效应模型代码（针对自选择偏差）

---

1.Heckman模型的由来

Heckman模型的提出是为了解决样本选择偏差问题sample selection bias。样本选择偏差是选择偏差selection bias的一种，还有一种是自选择偏差self selection bias。这两种选择偏差的区别在于两者导致估计偏误的非随机选择机制不同。

a.样本选择偏差。样本选择偏差的非随机选择机制指对样本的选择不是随机的，由研究者根据研究需求选定，同时，也可以认为是被解释变量y是非随机的。如研究妇女年龄与工资收入的关系，虽然我们可以观测到有工作的妇女的实际工资收入，但是不知道没有工作的妇女的“保留工资”（即愿意工作的最低工资）。于是我们收集数据时就会缺失没有工作的妇女样本。被选定的样本不能代表总体，最终导致估计偏误。对于上述例子，产生的偏误如下图所示：

b.自选择偏差。自选择偏差的非随机选择机制指对解释变量x的选择是非随机的，受到个体（指研究对象，如家庭、企业、国家或地区等）特征的影响，某些影响被解释变量并影响核心解释变量的因素无法穷尽，或者不可观测或则不可影响形式未知，这些因素在某些计量书中也被称为混杂因素，即会同时影响解释变量和被解释变量的因素。如研究上大学对收入的影响，我们将上大学的和没上大学的人进行简单比较，会发现大学生的平均工资比没上过大学的人的平均工资高。事实上，这种简单比较就存在严重的自选择问题，因为在这里比较的两类人在自身特质方面可能存在很大差异，上大学的孩子可能本身就很出色（更聪明、有毅力、能力强...），从而使得他们更有可能考上大学，并且更有可能获得更高的收入。这些因素若未被考虑，会导致核心解释变量与扰动项相关，使得估计量偏误。

若是想严格考察上大学对收入的影响，就要保证上大学与未上大学的样本在智力、能力、家庭背景等各方面条件一致，即自选择时要控制这问题，把两组样本的区别控制在是否上大学这点上。因而在存在自选择问题时，一般使用PSM（倾向得分）和DID（双重差分法）等方法。（这个以后再学）

2.选择偏差、样本选择偏差、自选择偏差与遗漏变量误差

a.样本选择偏差与自选择偏差：如前所述，两者差别在于非随机选择机制不同。前者是样本的选择存在非随机性，导致被解释变量y的非随机（因为一部分样本未被选入研究，则无法获得相应的y）。后者是解释变量x的选择存在非随机性。另外，样本选择偏差中，个体差异在于是否有机会进入到观测样本，那些未进入样本的个体，其y是观测不到的；而在自选择偏误中，个体的差异在于是否得到处理，并且这种差异是个体自选择形成的，而不论是否得到处理，其y都是可观测的。

b.自选择偏差与遗漏变量误差：自选择偏差与遗漏变量偏差很相像。一般认为自选择偏差是导致遗漏变量误差产生的一个常见来源。

c.选择偏差与遗漏变量偏差：关于这个问题的讨论，在选择性偏误（selection bias）与样本选择偏差（sample self-selction）一样吗 - Stata专版 - 经管之家(原人大经济论坛)也找到了一些精彩的回答。有答主认为，区分选择偏差与遗漏变量误差在于看这个变量是否存在。遗漏的前提是变量存在，若是变量存在或可观测却未被考虑到，则属于遗漏变量；若变量本身不存在或不可观测，则不属于遗漏变量，而应该是选择偏差。从这个角度看，遗漏变量问题可以通过加入变量解决，而选择偏差问题不可以。

3.样本选择模型与处理效应模型

针对样本选择偏差问题采用样本选择模型，一般采用的就是Heckman模型（还有起初的Heckit，未了解），针对自选择偏差问题则采用的处理效应模型，处理效应模型是基于Heckman两阶段模型而设计的，两者结构相似，但是本质不同。

a.Heckman两阶段模型/样本选择模

Heckman两阶段包括样本选择阶段与检验结果阶段（有博主称第二阶段为处理效应阶段，但不同于解决自选择偏差的处理效应模型）。样本选择阶段应用选择方程模型，用于分析样本的选择行为（例如，妇女是否选择工作D=1或0），检验结果阶段应用结果方程模型。

仍以妇女受教育水平与工资收入的研究为例，初始回归模型为

                       （1）

模型中，X为控制变量向量，D为内生的指示变量（虚拟变量），表示

再考虑样本选择偏误问题，引入Heckman模型后，首先，利用全部样本通过选择方程模型分析样本选择倾向：

                  （2）

利用probit模型进行回归。 其中，Z是会影响D，但不直接影响Y的变量，被称为排他性约束变量，可以看作是一种工具变量，因此也需要满足相关性和外生性的条件。另外，如果原模型是普通DID模型，则应避免选用D的滞后项作为工具变量Z,否则会导致多重共线性，这里Heckman两步法 | 样本选择模型 & 处理效应模型_KEMOSABEr的博客-CSDN博客_样本选择模型有具体解释。

通常，式（1）和式（2）的随机误差项（扰动项）u和v互不相关，两者服从二元正态分布，但若二者协方差不为0，则会导致式子（1）中D的系数估计有偏。

Heckman的思想是通过式（2）构造逆米尔斯比率（Inverse Mill’s Ratio，IMR或λ）来控制这个偏差。公式如下：

                  （3）

其中，是第i个样本在第一步回归（选择方程）的拟合值，为标准正态概率密度函数pdf，为累计分布函数cdf。

然后，将逆米尔斯比率IMR加入初始回归方程构成结果方程模型，并对选定的样本进行回归：

            （4）

至此，随机误差项与指示变量D不相关，为无偏估计量。另外，可以通过IMR系数的显著性与符号来判断样本选择偏差是否存在及其方向。

简单来说，Heckman模型两步估计步骤如下：

   —第一步，利用全部妇女（工作的和未工作的）中随机抽取的样本，估计妇女工作倾向模型；并利用估计结果，计算每个样本的逆米尔斯IMR值；

   —第二步，利用选定的样本观测值（工作的妇女样本数据）和计算得到的逆米尔斯比的值,将()作为一个待估计参数，估计妇女工资模型,得到的估计。 

   —注意，在抽取样本时间必须保证所有选择性样本包含于全部样本之中。

逆米尔斯比率IMR能够识别估计量的偏误，主要是通过：

（1）IMR是X 和Z 变量的非线性函数

（2）Z变量从处理效应模型方程式 (4) 中已经排除

至此来看，样本选择偏差可以看作是因遗漏了变量IMR而导致的内生性问题。

需要注意的是，将IMR放入第二阶段可能会造成多重共线问题，因此需要在回归结果中报告VIFs（Variance Inflaction Factors）。通常认为VIFs值超过10，即存在多重共线问题。

b.处理效应模型

     处理效应模型是用来缓解自选择偏差问题的，而自选择偏差与遗漏变量误差很相似。因此，自选择偏差也可以看作是遗漏了重要变量形成的内生性问题，这个变量就是逆米尔斯比率IMR。由于，处理效应模型本身是基于Heckman两阶段模型构建的，因此在结构上很相像，第一步都是用指示变量D对控制变量X与一个或多个工具变量Z进行回归，并计算IMR；第二步，将第一步计算的IMR放入原回归方程，重新回归估计核心解释变量的系数。区别在于IMR的计算方式不同。Heckman模型只计算指定样本的IMR，而处理效应模型计算全样本的IMR：

       （5）

还有一定需要注意的是，不同于样本选择模型，处理效应模型回归的是全样本，因此此时指示变量D不应有缺失值。

另外，样本选择模型和处理效应模型都要注意到一点是：第一步回归都只能用probit，而不能用logit模型。这是因为Heckman模型假定选择方程的随机误差项服从正态分布。PSM（倾向得分模型）则对于probit和logit模型均可以用。然而，选择方程使用probit模型进行估计有一个问题就是probit（包括Stata的xtprobit）不能估计固定效应模型，因此即便在回归方程中引入时间虚拟变量和个体虚拟变量，控制的也只是“时间效应”和“个体效应”，不能加入“固定”二字。

4.模型的Stata实现

 两个模型均可以使用极大似然估计MLE和常规两步法实现。常见的用于说明样本选择模型（Heckman模型，针对样本选择偏差）的案例妇女受教育水平对工资的影响；用于说明处理效应模型（针对自选择偏差）是工会主义对工资的影响研究（工人决定是否加入工会的行为是内生的，不可观测的因素如智力、人脉等会影响工人加入工会的决定，但这种不可观测因素也可以影响未来的工资）。 在前述参考的博文Heckman两步法 | 样本选择模型 & 处理效应模型_KEMOSABEr的博客-CSDN博客_样本选择模型（详细）和学习笔记 | Heckman两阶段法介绍_Claire_chen_jia的博客-CSDN博客_heckman两阶段中都有通过公开数据与Stata代码，并利用结果复盘。

这些公开数据与代码部分来自data01/Heckman_How_to_Use.do · 连享会/data - Gitee.com。

（题外话：打开Gitee发现这个一个强大的论坛，里面有许多数据与模型代码是公开可得的。点赞！）

a.样本选择模型代码（针对样本选择偏差）

*--------------样本选择模型-------------
use "C:\Users\AN\Downloads\womenwk.dta", clear //根据数据存储路径导入数据

*ols
reg wage educ age
est store OLS

*heckman maximum likelihood
heckman wage educ age, select(married children educ age) //默认最大似然估计
est store HeckMLE

*heckman two-step  all-in-one 不可以进行cluster（聚类）调整
heckman wage educ age, select(married children educ age) twostep
est store Heck2s

*heckman two-step  step-by-step 可以进行cluster（聚类）调整
probit work married children educ age //利用全样本数据进行选择倾向回归
est store First
predict y_hat, xb //这个命令跟predict Yhat得出的结果一致，只不过带上xb是用来区分resid；
             //带上xb，表示得出的y值，而带上resid得出的是残差值，以此来说明，也更容易记清与比较
gen pdf = normalden(y_hat)  //概率密度函数
gen cdf = normal(y_hat)     //累积分布函数
gen imr = pdf/cdf           //利用全样本数据计算逆米尔斯比率
reg  wage educ age imr if work == 1  //选定工作的女性样本进行结果效应回归
est store Second
vif  //方差膨胀因子

*对比结果
local m "OLS HeckMLE Heck2s First Second"  //local将引号内字符串存储在局部宏m中
esttab `m', mtitle(`m') nogap compress pr2 ar2

b.处理效应模型代码（针对自选择偏差）

*--------------处理效应模型-------------
use union3.dta, clear  //这里要根据数据存储路径导入数据

*ols
reg wage age grade smsa black tenure union
est store OLS

*etregress maximum likelihood
etregress wage age grade smsa black tenure,  ///etregress命令与heckman命令很相似
	  treat(union = south black tenure) twostep 
est store etrMLE

*etregress two-step all-in-one  不可以进行cluster调整
etregress wage age grade smsa black tenure,  ///
		  treat(union = south black tenure) twostep 
est store etr2s	

*etregress two-step  step-by-step 可以进行cluster调整
probit union south black tenure
est store First
predict y_hat, xb
gen pdf = normalden(y_hat)
gen cdf = normal(y_hat)
gen imr1 = pdf/cdf            //union = 1算法
gen imr2 = (-pdf) / (1 - cdf) //union = 0算法，加入工会的与未加入的计算IMR方式不一样
gen imr = imr1 
replace imr = imr2 if union == 0
reg wage age grade smsa black tenure union imr  //对所有样本进行结果回归，而非只是选定的样本
est store Second
vif  

*对比结果
local m "OLS etrMLE etr2s First Second"
esttab `m', mtitle(`m') nogap compress pr2 ar2

处理效应模型在Stata第14版之后的官方命令是etregress，与heckman类似，etregress同样可以进行处理效应模型的两步法估计和极大似然估计。

上述代码比较简单，但是可以学习其他博主的分析，Heckman两步法 | 样本选择模型 & 处理效应模型_KEMOSABEr的博客-CSDN博客_样本选择模型对不同模型的比较分析非常详细，还介绍了MLE估计+异方差稳健标准误进行模型回归。

另外，在查找资料的过程中，搜到了一个处理内生性问题的新命令eregress，有看到这篇博文的朋友，感兴趣可以了解一下Stata学习：内生性处理新命令eregress - Stata专版 - 经管之家(原人大经济论坛)。