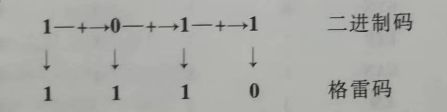FPGA与数字IC求职知识准备 - 数字电路知识总结
前言
本文整理了数字电路课程中的相关基本的知识点和较为重要的知识点,用于求职的数电部分的知识准备,差缺补漏。
二进制数的算术运算
无符号二进制数的算术运算
加法:同十进制加法,逢二进一,无符号二进制数的加法运算是基础。
减法:同十进制减法,不够减借位。
乘法:乘法运算是由左移被乘数与加法运算组成的。
除法:乘法运算是由右移除数与减法运算组成的。
带符号二进制数的算术运算
为了简化带二进制数进行减法运算,数字电路中负数通常是用补码进行表示,因此,引入了二进制数的补码的概念。
带符号二进制数的补码、反码计算方法如下:
- 补码与反码的最高位为符号位,正数为0,负数为1。
- 当二进制数为正数时,补码、反码与原码相同。
- 当二进制数为负数时,原码的数值位(不包含符号位),逐位取反即得到反码;然后将反码加一得到带符号二进制负数的补码。
数据溢出问题
数据在进行加减法时可能会造成数据的溢出,两个符号相同的数相加会造成溢出,两个符号相反的数相加不会造成溢出,解决方法是进行位拓展。
数制问题
二-十进制编码
二-十进制编码就是用4位二进制数来表示1位十进制数中的0-9的十个数码,即二进制编码的十进制码(BCD码)。
常见的BCD码分为有权码和无权码。
有权码:8421码,2421码,5421码等。
无权码:余三码,余三循环码(将格雷码首尾三种状态去掉的编码)。
十进制与N进制转换
N进制数转换为十进制数:按其位权展开,然后相加,得到相应的十进制数。
十进制数转化为N进制数:整数部分,除R取余法,除到商为0为止。小数部分,乘R取整法,乘到积为0为止。
格雷码与二进制转换
格雷码也是一种常见的无权码。
二进制与格雷码转换:
- 格雷码的最高位(最左边)与二进制码的最高位相同。
- 从左到右,逐一将二进制码相邻两位相加(舍去进位),作为格雷码的下一位。
下图例子将二进制码1011转换为格雷码1110。
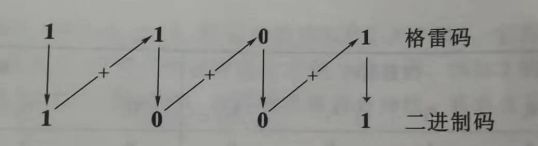
格雷码与二进制转换:
- 二进制的最高位(最左边)与二进制码的最高位相同。
- 将产生的每一位二进制码,与下一位相邻的格雷码相加(舍去进位),作为二进制码的下一位。
下图例子将格雷码1101转换为二进制码1001。
十六进制与八进制转换
二进制数与十六进制数互相转换:以小数点为基准,整数部分四位一组,不足四位的高位补零,小数部分四位一组,不足四位的低位补零。反之亦成立。
二进制数与八进制数互相转换:以小数点为基准,整数部分三位一组,不足三位的高位补零,小数部分三位一组,不足三位的低位补零。反之亦成立。
逻辑函数
描述逻辑输入变量和逻辑输出变量之间的因果关系称为逻辑函数。
表示方法
几种常见的逻辑函数表示方式:
- 真值表
- 逻辑函数表达式
- 逻辑图
- 波形图
- 卡诺图
- HDL
真值表与逻辑图转换
通常从给定的真值表不能直接得到逻辑图。首先根据真值表写出逻辑表达式,依照逻辑表达式画出逻辑图,转换步骤如下:
- 根据真值表写出逻辑表达式。
- 用公式法或卡诺图法化简得到简化的逻辑表达式。
- 根据逻辑表达式画出逻辑图。
逻辑图到真值表的转换
从逻辑图不能直接得到真值表,转换步骤如下:
- 从逻辑图的输人端到输出端,逐级写出每个逻辑符号输出端的表达式,直到写出最后输出变量的逻辑表达式。
- 化简变换,求简化的逻辑表达式。
- 将输人变量可能的取值逐个代入表达式进行计算,并将结果列表,即得真值表。
逻辑代数
逻辑代数有一系列的定理、定律、规则,用数学表达式进行处理,完成对逻辑电路的化简、变化、分析与总结。
简单的代数定律不在赘述,同数学代数中的交换律、结合律、分配律、吸收律。
反演律,又叫摩根定律,可实现与非式转换非或式,或非式转换非与式的互换。
与非式转换非或式:
A ⋅ B ‾ = A ˉ + B ˉ \overline {A·B}= \bar A +\bar B A⋅B=Aˉ+Bˉ
或非式转换非与式:
A + B ‾ = A ˉ ⋅ B ˉ \overline {A+B}= \bar A ·\bar B A+B=Aˉ⋅Bˉ
其他常见恒等式:
A + A ˉ ⋅ B = A + B A ⋅ B + A ˉ ⋅ C + B ⋅ C = A ⋅ B + A ˉ ⋅ C A\ + \bar A ·B = A + B\\ A · B\ + \bar A · C + B·C = A · B\ + \bar A · C A +Aˉ⋅B=A+BA⋅B +Aˉ⋅C+B⋅C=A⋅B +Aˉ⋅C
逻辑函数表达式基本形式
与或式:值若干与项进行或的逻辑运算构成的表达式,简称与或式,或者称为积之和式(SOP)。
或与式:值若干或项进行与的逻辑运算构成的表达式,简称或与式,或者称为积之和式(POS)。
最小项与最小项表达式
最小项:对于n个变量的逻辑函数,若有一个乘积项包含了全部的n个变量,每个变量都以他的原变量或者非变量的形式出现在乘积项中,且仅出现一次,则该乘积项为最小项。例如变量A、B,最小项有AB,AB非,A非B,A非B非,而A,B这些项不是最小项。
最小项性质:
- 输入任意一个最小项,只有一组取值使得结果为1,其余各组取值均为0。
- 任意两个不同最小项积为0。
- 所有最小项的和为1。
最小项表达式:由若干最小项进行或操作构成的逻辑表达式,也称为标准与或式。任意一个逻辑函数都能变换成唯一的最小项表达式。
最大项与最大项表达式
最大项:对于n个变量的逻辑函数,若有一个或项包含了全部的n个变量,每个变量都以他的原变量或者非变量的形式出现在或项中,且仅出现一次,则该或项为最大项。
最大项性质:
- 输入任意一个最大项,只有一组取值使得结果为0,其余各组取值均为1。
- 任意两个不同最大项和为1。
- 所有最小项的积为0。
卡诺图化简
卡诺图化简步骤:
- 将逻辑函数写成最小项表达式。
- 将最小项表达式填入卡诺图中。
- 找出为1的相邻最小项,画包围圈,写出每个包围圈的乘积项。
- 将所有包围圈对应的乘积项相加。
画包围圈的原则:
- 包围圈内的方格数必须是2的n次方个。
- 相邻方格包括上下底相邻,左右边相邻,四角两两相邻。
- 同一个方格可被多个不同的包围圈重复包围,但新增的包围圈中一定要有新的方格。
- 包围圈的方格数要尽量多,包围圈数目要尽可能少。
逻辑门电路抗干扰措施
利用逻辑门电路(CMOS或者TTL)设计电路时需要注意干扰的处理,需要注意以下方面。
- 多余输入端的处理措施:一般不让多余的输入端悬空,以防引入干扰信号。或门或者或非门的多余的输入端可以接地;与门或者与非门的多余输入端通过上拉电阻接电源,对于CMOS电路可直接接电源。
- 电路适当放置去耦合滤波电容:可滤除干扰信号。
- 接地处理:通常在电路设计中会将电源地和信号地分开,将信号地汇集一点,然后将二者用最短的导线连在一起。
组合逻辑电路
定义、特点、分析方法
组合逻辑电路定义:对于一个逻辑电路,其输出状态在任何时刻只取决于同一时刻的输入状态,而与电路原来的状态无关,这种电路被定义为组合逻辑电路。
组合逻辑电路特点:
- 输入、输出之间没有反馈延时通路。
- 电路中不含有记忆功能的元件。
组合逻辑电路的分析方法
- 根据逻辑电路,写出各级的逻辑表达式,整理得到输出信号和输入信号的逻辑表达式。
- 将逻辑表达式化简、变换,得到最简单的表达式。
- 根据化简后的逻辑表达式写出真值表。
- 根据真值表和化简后的表达式分析逻辑电路,确定其功能。
竞争-冒险现象
由于实际电路中的信号传输都存在延时,在电平变化时,可能存在和瞬态下的逻辑功能不一致,产生错误输出,这种现象就是竞争-冒险。
竞争:一个逻辑门两个输入端的信号同时向相反方向变化,而变化的时间有差异的现象,称为竞争。
冒险:由竞争而可能产生输出干扰脉冲的现象称为冒险。
竞争-冒险现象解决办法
- 发现并消去互补相乘项
- 增加乘积项以避免互补项相加
- 输出端并联电容器
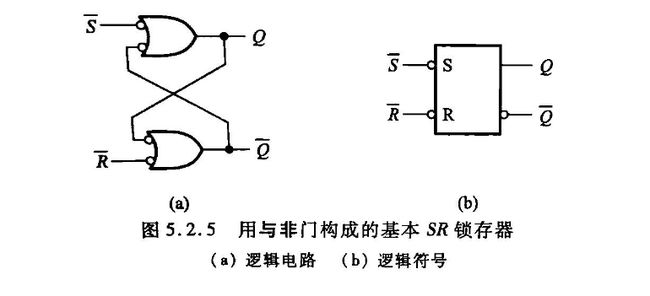
锁存器
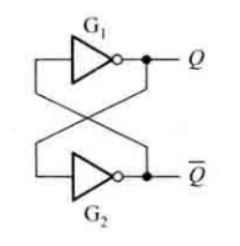
双稳态存储电路(双稳态电路):具有0、1两种逻辑状态,一旦进入其中一种状态,就能长期保持不变的单元电路叫做双稳态存储电路,简称双稳态电路。下图是使用非门构成的最基本的双稳态电路。
基本SR锁存器
**锁存器(Latch)**是一种脉冲电平敏感的双稳态电路,具备0和1两个稳定状态,一旦状态被确定,就可自行保持,直到外部特定输入脉冲电平作用在电路的一定位置时,才有可能改变状态。
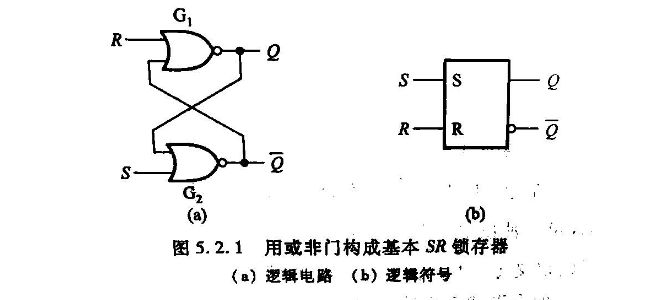
将上述的最简单的双稳态电路中的非门换成或非门或者与非门,构成下图所示的电路是基本SR锁存器。
或非门构成的SR锁存器
或非门构成的SR锁存器功能表
| S | R | Q | !Q | 功能 |
|---|---|---|---|---|
| 0 | 0 | 不变 | 不变 | 保持 |
| 0 | 1 | 0 | 1 | 置0 |
| 1 | 0 | 1 | 0 | 置1 |
| 1 | 1 | 0 | 0 | 非定义状态 |
与非门构成的SR锁存器
与非门构成的SR锁存器功能表
| !S | !R | Q | !Q | 功能 |
|---|---|---|---|---|
| 1 | 1 | 不变 | 不变 | 保持 |
| 1 | 0 | 0 | 1 | 置0 |
| 0 | 1 | 1 | 0 | 置1 |
| 0 | 0 | 0 | 0 | 非定义状态 |
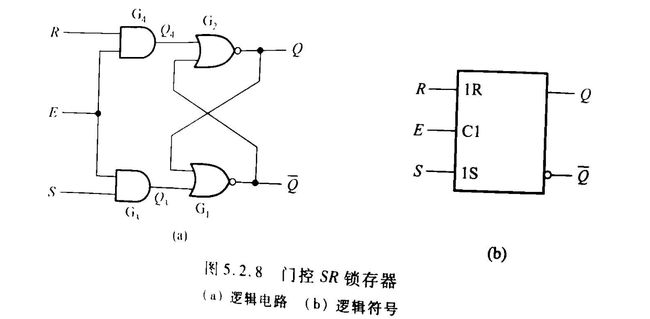
门控SR锁存器
D锁存器
与SR锁存器不同,D锁存器在工作中不存在非定义状态。
D锁存器的功能表
| E | D | Q | !Q | 功能 |
|---|---|---|---|---|
| 0 | X | 不变 | 不变 | 保持 |
| 1 | 0 | 0 | 1 | 置0 |
| 1 | 1 | 1 | 0 | 置1 |
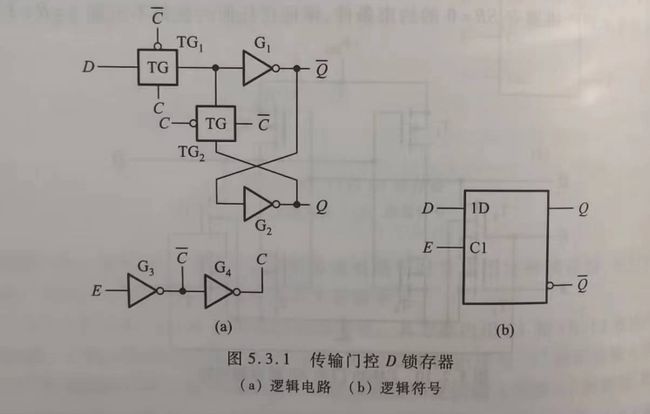
传输门控D锁存器
传输门控D锁存器是最基本的双稳态电路的基础上增加两个传输门。
逻辑门控D锁存器
触发器
对时钟脉冲边沿敏感的状态更新称为触发。具备触发工作特性的存储单元称为触发器。
D触发器
D触发器的特征表如下,
| D | Q^(n) | Q^(n+1) |
|---|---|---|
| 0 | 0 | 0 |
| 0 | 1 | 0 |
| 1 | 0 | 1 |
| 1 | 1 | 1 |
特性方程:
Q n + 1 = D Q^{n+1}=D Qn+1=D
JK触发器
JK触发器的特征表如下,
| J | K | Q^(n) | Q^(n+1) |
|---|---|---|---|
| 0 | 0 | 0 | 0 |
| 0 | 0 | 1 | 1 |
| 0 | 1 | 0 | 0 |
| 0 | 1 | 1 | 0 |
| 1 | 0 | 0 | 1 |
| 1 | 0 | 1 | 1 |
| 1 | 1 | 0 | 1 |
| 1 | 1 | 1 | 0 |
特性方程:
Q n + 1 = J Q n ‾ + K ‾ Q n Q^{n+1}=J\overline{Q^{n}}+\overline{K}{Q^{n}} Qn+1=JQn+KQn
JK触发器特点:
- JK均置位为0时,状态保持。
- JK均置位为1时,状态翻转。
- J置位为1,K置位为0,次态置位为1。
- J置位为0,K置位为1,次态置位为0。
T触发器
T触发器的特征表如下,
| T | Q^(n) | Q^(n+1) |
|---|---|---|
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 0 |
特性方程:
Q n + 1 = T ⊕ Q n Q^{n+1}=T⊕{Q^{n}} Qn+1=T⊕Qn
JK触发器特点:当控制信号T=1时,每来一个脉冲,状态翻转一次,当T=0时,输出状态保持不变。
T’触发器
当T触发器的T固定接入高电平时,即T=1,特征方程变为。
Q n + 1 = Q n ‾ Q^{n+1}=\overline{Q^{n}} Qn+1=Qn
SR触发器
SR触发器的特征表如下,
| S | R | Q^(n) | Q^(n+1) |
|---|---|---|---|
| 0 | 0 | 0 | 0 |
| 0 | 0 | 1 | 1 |
| 0 | 1 | 0 | 0 |
| 0 | 1 | 1 | 0 |
| 1 | 0 | 0 | 1 |
| 1 | 0 | 1 | 1 |
| 1 | 1 | 0 | 不确定 |
| 1 | 1 | 1 | 不确定 |
类似,SR锁存器的功能。
时序逻辑电路
时序逻辑电路
由组合电路和存储电路组成,时序电路的状态和时间因素相关,即时序电路的任一时刻的状态变量不仅是输入信号的函数,而且还是电路以前状态变量的函数,并且当前输入变量和状态决定电路的下一状态。时序电路的输出信号由输入信号和电路状态共同决定。
异步时序电路
电路没有统一的时钟,有些触发器的时钟输入端与时钟脉冲源相连,这些触发器的状态变化与时钟脉冲同步,而有些触发器的状态变化不与时钟脉冲同步。存储电路的状态转换因为存在时间差异而可能造成短时间输出状态的不确定,而且这种不确定的状态有时是不容易判断的。
同步时序电路
存储电路中所有触发器的时钟输入端都接同一个时钟脉冲源,因而所有触发器的状态的变化都与所加的时钟脉冲信号同步。
状态机
状态机就是能够根据控制信号按照预先设定的状态进行状态转移,是协调相关信号动作、完成特定动作的控制中心。状态机简写为 FSM (Finite State Machine)。
Moore型状态机时序电路:输出只和当前状态有关而与输入无关。
Mealy型状态机时序电路:输出不仅和当前状态有关而且和输入有关。
时序逻辑电路功能的表达
逻辑方程组、转换表、状态表、状态图、时序图。
同步时钟的时钟偏移的原因
- 各触发器时钟传输路径上的长度不同;
- 各触发器时钟传输路径上的经过的缓冲器的数量不同;
- 各触发器时钟传输路径上的负载不平衡。