mean value coordinates(均值重心坐标)定义及证明
欢迎关注更多精彩
关注我,学习常用算法与数据结构,一题多解,降维打击。
在图形学中对于物体的描述往往是离散,但是在具体展示过程中我们又希望是连续。线性插值是解决离散与连续的常用手段。
- 三角形中的插值点击前往
- 凸四边形中的插值点击前往
本文是针对多边形的插值
均值坐标定义
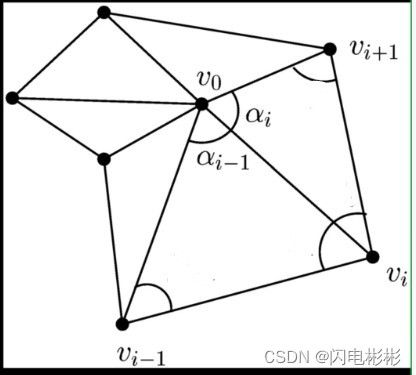
v 0 是多边形 v 1 v 2 v 3 . . . v n 内的一点 v_0是多边形v_1v_2v_3...v_n内的一点 v0是多边形v1v2v3...vn内的一点
就会存在均值坐标 ϕ i ( v 0 ) = ω i ∑ j = 1 n ω j 就会存在均值坐标\phi_i(v_0)=\frac {\omega_i}{\sum_{j=1}^n\omega_j} 就会存在均值坐标ϕi(v0)=∑j=1nωjωi
其中 ω i = t a n ( α i − 1 2 ) + t a n ( α i 2 ) ∣ ∣ v i − v 0 ∣ ∣ 其中\omega_i=\frac {tan \left(\frac {\alpha_{i-1}}{2} \right)+tan \left(\frac {\alpha_{i}}{2} \right)}{||v_i-v_0||} 其中ωi=∣∣vi−v0∣∣tan(2αi−1)+tan(2αi)
使得
v 0 = ∑ i = 1 n ϕ i ( v 0 ) ⋅ v i … … ( 1 ) v_0=\displaystyle \sum_{i=1}^n\phi_i(v_0)\cdot v_i ……(1) v0=i=1∑nϕi(v0)⋅vi……(1)
证明mvc为广义重心坐标
要求证明式子(1)成立。
根据定义可知
∑ i = 1 n ϕ i ( v 0 ) = 1 \displaystyle \sum_{i=1}^n\phi_i(v_0) = 1 i=1∑nϕi(v0)=1
那么通过移项可以得到
∑ i = 1 n ϕ i ( v 0 ) ⋅ ( v i − v 0 ) = 0 … … ( 2 ) \displaystyle \sum_{i=1}^n\phi_i(v_0)\cdot (v_i-v_0)=0……(2) i=1∑nϕi(v0)⋅(vi−v0)=0……(2)
问题转化成证明式子(2)

引入极坐标定义
向量 v i − v 0 与水平夹角为 θ i 向量v_i-v_0与水平夹角为\theta_i 向量vi−v0与水平夹角为θi
则 α i = θ i + 1 − θ i 则\alpha_i = \theta_{i+1}-\theta_i 则αi=θi+1−θi
v i = v 0 + ∣ ∣ v i − v 0 ∣ ∣ ( c o s θ i , s i n θ i ) v_i=v_0+||v_i-v_0||(cos\theta_i,sin\theta_i) vi=v0+∣∣vi−v0∣∣(cosθi,sinθi)
= = > v i − v 0 ∣ ∣ v i − v 0 ∣ ∣ = ( c o s θ i , s i n θ i ) … … ( 3 ) ==>\frac {v_i-v_0}{||v_i-v_0||} = (cos\theta_i,sin\theta_i) ……(3) ==>∣∣vi−v0∣∣vi−v0=(cosθi,sinθi)……(3)
将(2)式展开
∑ i = 1 n t a n ( α i − 1 2 ) + t a n ( α i 2 ) ∣ ∣ v i − v 0 ∣ ∣ ∑ j = 1 n ω j ⋅ ( v i − v 0 ) = 0 \displaystyle \sum_{i=1}^n\frac {\frac {tan \left(\frac {\alpha_{i-1}}{2} \right)+tan \left(\frac {\alpha_{i}}{2} \right)}{||v_i-v_0||}}{\sum_{j=1}^n\omega_j}\cdot (v_i-v_0)=0 i=1∑n∑j=1nωj∣∣vi−v0∣∣tan(2αi−1)+tan(2αi)⋅(vi−v0)=0
两边都乘以 ∑ j = 1 n ω j 两边都乘以{\sum_{j=1}^n\omega_j} 两边都乘以∑j=1nωj
∑ i = 1 n [ t a n ( α i − 1 2 ) + t a n ( α i 2 ) ] ⋅ v i − v 0 ∣ ∣ v i − v 0 ∣ ∣ = 0 \displaystyle \sum_{i=1}^n \left[ tan \left(\frac {\alpha_{i-1}}{2} \right)+tan \left(\frac {\alpha_{i}}{2} \right) \right]\cdot\frac {v_i-v_0}{||v_i-v_0||}=0 i=1∑n[tan(2αi−1)+tan(2αi)]⋅∣∣vi−v0∣∣vi−v0=0
将(3)式代入得到
∑ i = 1 n [ t a n ( α i − 1 2 ) + t a n ( α i 2 ) ] ⋅ ( c o s θ i , s i n θ i ) = 0 \displaystyle \sum_{i=1}^n \left[ tan \left(\frac {\alpha_{i-1}}{2} \right)+tan \left(\frac {\alpha_{i}}{2} \right) \right]\cdot(cos\theta_i,sin\theta_i) =0 i=1∑n[tan(2αi−1)+tan(2αi)]⋅(cosθi,sinθi)=0
求和项拆开
∑ i = 1 n t a n ( α i − 1 2 ) ⋅ ( c o s θ i , s i n θ i ) + ∑ i = 1 n t a n ( α i 2 ) ⋅ ( c o s θ i , s i n θ i ) = 0 \displaystyle \sum_{i=1}^n tan \left(\frac {\alpha_{i-1}}{2} \right ) \cdot(cos\theta_i,sin\theta_i)+\displaystyle \sum_{i=1}^n tan \left(\frac {\alpha_{i}}{2} \right) \cdot(cos\theta_i,sin\theta_i)=0 i=1∑ntan(2αi−1)⋅(cosθi,sinθi)+i=1∑ntan(2αi)⋅(cosθi,sinθi)=0
变换i-1下标到i得到
∑ i = 1 n t a n ( α i 2 ) ⋅ ( c o s θ i + 1 , s i n θ i + 1 ) + ∑ i = 1 n t a n ( α i 2 ) ⋅ ( c o s θ i , s i n θ i ) = 0 \displaystyle \sum_{i=1}^n tan \left(\frac {\alpha_{i}}{2} \right ) \cdot(cos\theta_{i+1},sin\theta_{i+1})+\displaystyle \sum_{i=1}^n tan \left(\frac {\alpha_{i}}{2} \right) \cdot(cos\theta_i,sin\theta_i)=0 i=1∑ntan(2αi)⋅(cosθi+1,sinθi+1)+i=1∑ntan(2αi)⋅(cosθi,sinθi)=0
再合并,替换 α i 再合并,替换\alpha_i 再合并,替换αi
∑ i = 1 n t a n ( θ i + 1 − θ i 2 ) ⋅ ( c o s θ i + 1 + c o s θ i , s i n θ i + 1 + s i n θ i ) = 0 … … ( 4 ) \displaystyle \sum_{i=1}^n tan \left(\frac {\theta_{i+1}-\theta_i}{2} \right ) \cdot(cos\theta_{i+1}+cos\theta_{i},sin\theta_{i+1}+sin\theta_{i})=0……(4) i=1∑ntan(2θi+1−θi)⋅(cosθi+1+cosθi,sinθi+1+sinθi)=0……(4)
现在需要证明式子(4)成立。
基本思路是能够把两个三角函数加和转化成一个三角函数并且伴有半角的出现。
通过翻阅资料找到以下几个公式。
tanα=sinα/cosα
sinα+sinβ=2sin[(α+β)/2]cos[(α-β)/2]
sinα-sinβ=2cos[(α+β)/2]sin[(α-β)/2]
cosα+cosβ=2cos[(α+β)/2]cos[(α-β)/2]
cosα-cosβ=-2sin[(α+β)/2]sin[(α-β)/2]
继续化简
∑ i = 1 n s i n ( θ i + 1 − θ i 2 ) c o s ( θ i + 1 − θ i 2 ) ⋅ [ 2 c o s ( θ i + 1 + θ i 2 ) c o s ( θ i + 1 − θ i 2 ) , 2 s i n ( θ i + 1 + θ i 2 ) c o s ( θ i + 1 − θ i 2 ) ] \displaystyle \sum_{i=1}^n \frac {sin\left(\frac {\theta_{i+1}-\theta_i}{2} \right )}{cos\left(\frac {\theta_{i+1}-\theta_i}{2} \right )} \cdot\left[2cos\left(\frac {\theta_{i+1}+\theta_i}2\right)cos\left(\frac {\theta_{i+1}-\theta_i}2\right),2sin\left(\frac {\theta_{i+1}+\theta_i}2\right)cos\left(\frac {\theta_{i+1}-\theta_i}2\right)\right] i=1∑ncos(2θi+1−θi)sin(2θi+1−θi)⋅[2cos(2θi+1+θi)cos(2θi+1−θi),2sin(2θi+1+θi)cos(2θi+1−θi)]
= ∑ i = 1 n [ 2 c o s ( θ i + 1 + θ i 2 ) s i n ( θ i + 1 − θ i 2 ) , 2 s i n ( θ i + 1 + θ i 2 ) s i n ( θ i + 1 − θ i 2 ) ] =\displaystyle \sum_{i=1}^n \left[2cos\left(\frac {\theta_{i+1}+\theta_i}2\right)sin\left(\frac {\theta_{i+1}-\theta_i}2\right),2sin\left(\frac {\theta_{i+1}+\theta_i}2\right)sin\left(\frac {\theta_{i+1}-\theta_i}2\right)\right] =i=1∑n[2cos(2θi+1+θi)sin(2θi+1−θi),2sin(2θi+1+θi)sin(2θi+1−θi)]
= ∑ i = 1 n ( s i n θ i + 1 − s i n θ i , − c o s θ i + 1 + c o s θ i ) = 0 =\displaystyle \sum_{i=1}^n (sin\theta_{i+1}-sin\theta_{i}, -cos\theta_{i+1}+cos\theta_{i})=0 =i=1∑n(sinθi+1−sinθi,−cosθi+1+cosθi)=0
经过化简后,正好首尾相接抵消。
故原式得证。
证毕。
本人码农,希望通过自己的分享,让大家更容易学懂计算机知识。
![]()