吴恩达深度学习第一课第四周作业（2）

当您完成本笔记本时，您将完成第4周的最后一个编程作业，以及课程1的最后一个编程作业！

要构建cat/not-a-cat分类器，您将使用前面分配的函数来构建深度网络。希望您能看到比以前的logistic回归实现在准确性方面有所提高。

完成此任务后，您将能够：
构建并训练了一个深层L层神经网络，并将其应用于监督学习
我们开始吧！

1-包

首先导入此任务期间需要的所有程序包。

-numpy是使用Python进行科学计算的基本包。
-matplotlib是一个用Python绘制图形的库。
-h5py是一个与存储在H5文件中的数据集交互的通用包。
-这里使用PIL和scipy测试您的模型，并在最后使用您自己的图片。
-dnn_app_utils提供了本笔记本“构建深层神经网络：一步一步”作业中实现的功能。
-seed（1）用于保持所有随机函数调用的一致性。它有助于你的工作等级-所以请不要改变它！

import time
import numpy as np
import h5py
import matplotlib.pyplot as plt
import scipy
from PIL import Image
from scipy import ndimage
from dnn_app_utils_v3 import *
from public_tests import *

%matplotlib inline
plt.rcParams['figure.figsize'] = (5.0, 4.0) # set default size of plots
plt.rcParams['image.interpolation'] = 'nearest'
plt.rcParams['image.cmap'] = 'gray'

%load_ext autoreload
%autoreload 2

np.random.seed(1)

2-加载和处理数据集

您将使用与“作为神经网络的逻辑回归”（作业2）中相同的“Cat与非Cat”数据集。你当时建立的模型在分类cat和非cat图像时有70%的测试准确率。希望你的新模型能表现得更好！
问题陈述：您将获得一个数据集（“data.h5”），其中包含：

-标记为cat（1）或non-cat（0）的“m_train”图像的训练集
-标记为cat和non-cat的“m_test”图像的测试集
-每个图像的形状（num_px，num_px，3），其中3表示3个通道（RGB）。

让我们更熟悉数据集。通过运行下面的单元格加载数据。

train_x_orig, train_y, test_x_orig, test_y, classes = load_data()

下面的代码将显示数据集中的图像。您可以随意更改索引并多次重新运行单元格以检查其他图像。

# 图片示例
index = 10
plt.imshow(train_x_orig[index])
print ("y = " + str(train_y[0,index]) + ". It's a " + classes[train_y[0,index]].decode("utf-8") +  " picture.")

运行结果：

y = 0. It's a non-cat picture.

# 浏览数据集 
m_train = train_x_orig.shape[0]
num_px = train_x_orig.shape[1]
m_test = test_x_orig.shape[0]

print ("训练集个数： " + str(m_train))
print ("测试集个数: " + str(m_test))
print ("每个图像的大小为： (" + str(num_px) + ", " + str(num_px) + ", 3)")
print ("train_x_orig 的形状: " + str(train_x_orig.shape)
print ("train_y 的形状: " + str(train_y.shape))
print ("test_x_orig 的形状: " + str(test_x_orig.shape))
print ("test_y shape: " + str(test_y.shape))

运行结果：

Number of training examples: 209
Number of testing examples: 50
Each image is of size: (64, 64, 3)
train_x_orig shape: (209, 64, 64, 3)
train_y shape: (1, 209)
test_x_orig shape: (50, 64, 64, 3)
test_y shape: (1, 50)

像往常一样，在将图像传送到网络之前，您需要对其进行重塑和标准化。代码在下面的单元格中给出。

图1

# 重塑培训和测试示例
train_x_flatten = train_x_orig.reshape(train_x_orig.shape[0], -1).T   # "-1" 是指将重塑成展平状态
test_x_flatten = test_x_orig.reshape(test_x_orig.shape[0], -1).T

# 标准化数据以使特征值介于0和1之间。
train_x = train_x_flatten/255.
test_x = test_x_flatten/255.

print ("train_x's shape: " + str(train_x.shape))
print ("test_x's shape: " + str(test_x.shape))

运行结果：

train_x's shape: (12288, 209)
test_x's shape: (12288, 50)

注：12288等于64×64×3，这是一个重塑图像矢量的大小。

3-模型架构

3.1 -2层神经网络

现在您已经熟悉了数据集，是时候建立一个深层次的神经网络来区分cat图像和non-cat图像了！
您将构建两个不同的模型：

-二层神经网络
-一种L层深度神经网络

然后，您将比较这些模型的性能，并为这些模型尝试一些不同的值 .
让我们看看这两种体系结构：
图2：双层神经网络。
模型可以概括为：输入->线性->RELU->线性->SIGMOID->输出。
图2的详细架构：

-输入是（64,64,3）图像，该图像被展平为大小为（12288,1）的向量。
-对应向量：[0,1,...,12287]  然后乘以权重矩阵[1] 大小([1],12288) .
-然后，添加一个偏差项并获取其relu以获得以下向量：[[1]0,[1]1,...,[1][1]−1] .
-重复同样的过程。
-将得到的向量乘以[2] 加上截距（偏差）。
-最后，取结果的sigmoid。如果大于0.5，则将其归类为cat。

3.2 -L层深层神经网络

用上述表示法来表示一个L层的深层神经网络是相当困难的。但是，这里有一个简化的网络表示：

图3的详细架构：

-输入是（64,64,3）图像，该图像被展平为大小为（12288,1）的向量。
-对应向量：[0,1,...,12287]  然后乘以权重矩阵[1] 然后加上截距[1] . 结果称为线性单位。
-接下来，取线性单位的relu。这一过程可以为每个人重复几次([],[])  取决于模型架构。
-最后，取最后一个线性单位的sigmoid。如果大于0.5，则将其归类为猫。

3.3 -一般方法

像往常一样，您将遵循深度学习方法来构建模型：

1.初始化参数/定义超参数
2.循环num_iterations次：
	a.正向传播 
	b.计算成本函数
	c.反向传播
	d.更新参数（使用参数和backprop的梯度）
3.使用经过训练的参数来预测标签

现在开始实施这两个模型！

4 -二层神经网络

练习1-两层模型

使用在上一个作业中实现的辅助函数来构建具有以下结构的2层神经网络：LINEAR->RELU->LINEAR->SIGMOID。功能及其输入为：

def initialize_parameters(n_x, n_h, n_y):
    ...
    return parameters 
def linear_activation_forward(A_prev, W, b, activation):
    ...
    return A, cache
def compute_cost(AL, Y):
    ...
    return cost
def linear_activation_backward(dA, cache, activation):
    ...
    return dA_prev, dW, db
def update_parameters(parameters, grads, learning_rate):
    ...
    return parameters

###定义模型的常量####
n_x = 12288     # num_px * num_px * 3
n_h = 7
n_y = 1
layers_dims = (n_x, n_h, n_y)
learning_rate = 0.0075

# GRADED FUNCTION: two_layer_model

def two_layer_model(X, Y, layers_dims, learning_rate = 0.0075, num_iterations = 3000, print_cost=False):
    """
    实现了两层神经网络：线性->RELU->线性->SIGMOID。
	参数：
	X——输入数据，形状（n×X，示例数）
	Y——真“标签”向量（如果是cat，则包含1；如果是非cat，则包含0），形状（1，示例数）
	层尺寸层的尺寸
	num_iterations—优化循环的迭代次数
	学习率——梯度下降更新规则的学习率
	print_cost——如果设置为True，这将每100次迭代打印一次成本
	返回：
	参数——包含W1、W2、b1和b2的字典
    """
    
    np.random.seed(1)
    grads = {}
    costs = []                              # 跟踪成本
    m = X.shape[1]                           # 示例数
    (n_x, n_h, n_y) = layers_dims
    
    # 通过调用以前实现的函数之一初始化参数字典
    #(≈ 1 line of code)
    # parameters = ...
    # 你的代码从这里开始
    parameters = initialize_parameters(n_x, n_h, n_y)
    # 你的代码到此结束
    
    # 从字典参数中获取W1、b1、W2和b2。
    W1 = parameters["W1"]
    b1 = parameters["b1"]
    W2 = parameters["W2"]
    b2 = parameters["b2"]
    
    # 循环（梯度下降）
    for i in range(0, num_iterations):

        # 正向传播：线性->RELU->线性->SIGMOID。输入：“X，W1，b1，W2，b2”。输出：“A1，cache1，A2，cache2”。
        #(≈ 两行代码)
        # A1, cache1 = ...
        # A2, cache2 = ...
        # 你的代码从这里开始
        A1,cache1 = linear_activation_forward(X, W1, b1, "relu")
        A2,cache2 = linear_activation_forward(A1, W2, b2, "sigmoid")        
        # 你的代码到此结束
        
        # 计算成本
        #(≈ 一行代码)
        # cost = ...
        # 你的代码从这里开始
        cost = compute_cost(A2, Y)
        
        # 你的代码到这结束
        
        # 初始化反向传播
        dA2 = - (np.divide(Y, A2) - np.divide(1 - Y, 1 - A2))
        
        # 反向传播。输入：“dA2，cache2，cache1”。输出：“dA1，dW2，db2；也包括dA0（未使用）、dW1、db1”。
        #(≈ 两行代码)
        # dA1, dW2, db2 = ...
        # dA0, dW1, db1 = ...
        # YOUR CODE STARTS HERE
        dA1, dW2, db2 = linear_activation_backward(dA2, cache2, "sigmoid")
        dA0, dW1, db1 = linear_activation_backward(dA1, cache1, "relu")
        # YOUR CODE ENDS HERE
        
        # 将grads['dWl']设置为dW1，grads['db1']设置为db1，grads['dW2']设置为dW2，grads['db2']设置为db2
        grads['dW1'] = dW1
        grads['db1'] = db1
        grads['dW2'] = dW2
        grads['db2'] = db2
        
        # 更新参数。
        #(大约1行代码)
        # parameters = ...
        # 你的代码从这里开始
        parameters = update_parameters(parameters, grads, learning_rate)
        
        # 你的代码到此结束

        # 从参数中检索W1、b1、W2、b2
        W1 = parameters["W1"]
        b1 = parameters["b1"]
        W2 = parameters["W2"]
        b2 = parameters["b2"]
        
        # 每100次迭代打印一次成本
        if print_cost and i % 100 == 0 or i == num_iterations - 1:
            print("Cost after iteration {}: {}".format(i, np.squeeze(cost)))
        if i % 100 == 0 or i == num_iterations:
            costs.append(cost)

    return parameters, costs

def plot_costs(costs, learning_rate=0.0075):
    plt.plot(np.squeeze(costs))
    plt.ylabel('cost')
    plt.xlabel('iterations (per hundreds)')
    plt.title("Learning rate =" + str(learning_rate))
    plt.show()

测试运行：

parameters, costs = two_layer_model(train_x, train_y, layers_dims = (n_x, n_h, n_y), num_iterations = 2, print_cost=False)

print("Cost after first iteration: " + str(costs[0]))

two_layer_model_test(two_layer_model)

测试结果：

Cost after iteration 1: 0.6926114346158595
Cost after first iteration: 0.693049735659989
Cost after iteration 1: 0.6915746967050506
Cost after iteration 1: 0.6915746967050506
Cost after iteration 1: 0.6915746967050506
所有测试都通过了。

4.1-培训模型

如果代码通过了上一个单元格，请运行下面的单元格来训练参数。

-每次迭代的成本都应该降低。
-运行2500次迭代可能需要5分钟。

parameters, costs = two_layer_model(train_x, train_y, layers_dims = (n_x, n_h, n_y), num_iterations = 2500, print_cost=True)
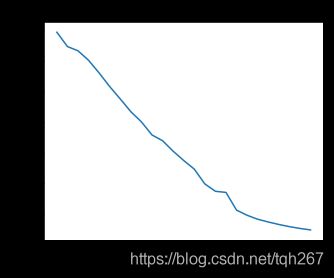
plot_costs(costs, learning_rate)

运行结果：

Cost after iteration 0: 0.693049735659989
Cost after iteration 100: 0.6464320953428849
Cost after iteration 200: 0.6325140647912677
Cost after iteration 300: 0.6015024920354665
Cost after iteration 400: 0.5601966311605747
Cost after iteration 500: 0.5158304772764729
Cost after iteration 600: 0.4754901313943325
Cost after iteration 700: 0.43391631512257495
Cost after iteration 800: 0.4007977536203886
Cost after iteration 900: 0.3580705011323798
Cost after iteration 1000: 0.3394281538366413
Cost after iteration 1100: 0.30527536361962654
Cost after iteration 1200: 0.2749137728213015
Cost after iteration 1300: 0.2468176821061484
Cost after iteration 1400: 0.19850735037466102
Cost after iteration 1500: 0.17448318112556638
Cost after iteration 1600: 0.1708076297809692
Cost after iteration 1700: 0.11306524562164715
Cost after iteration 1800: 0.09629426845937156
Cost after iteration 1900: 0.0834261795972687
Cost after iteration 2000: 0.07439078704319085
Cost after iteration 2100: 0.06630748132267933
Cost after iteration 2200: 0.05919329501038172
Cost after iteration 2300: 0.053361403485605606
Cost after iteration 2400: 0.04855478562877019
Cost after iteration 2499: 0.04421498215868956

很好！你成功地训练了模特。好在你建立了一个矢量化的实现！否则训练这个可能要花10倍的时间。
现在，可以使用经过训练的参数对数据集中的图像进行分类。要查看训练集和测试集上的预测，请运行下面的单元格。
训练集上：

predictions_train = predict(train_x, train_y, parameters)

运行结果：

Accuracy: 0.9999999999999998

测试集上：

predictions_test = predict(test_x, test_y, parameters)

运行结果：

Accuracy: 0.72

祝贺你！看来，你的两层神经网络有更好的表现（72%）比逻辑回归实施（70%，作业第二周）。让我们看看你是否能做得更好 -图层模型。
注意：您可能会注意到，以较少的迭代次数（比如1500次）运行模型可以提高测试集的准确性。这被称为“提前停车”，您将在下一节课中了解更多。提前停车是防止过度装配的一种方法。

五层神经网络

练习2-L_layer_model

使用先前实现的帮助器函数来构建 -具有以下结构的分层神经网络：[LINEAR->RELU]× (L-1）->线性->SIGMOID。功能及其输入为：

def initialize_parameters_deep(layers_dims):
    ...
    return parameters 
def L_model_forward(X, parameters):
    ...
    return AL, caches
def compute_cost(AL, Y):
    ...
    return cost
def L_model_backward(AL, Y, caches):
    ...
    return grads
def update_parameters(parameters, grads, learning_rate):
    ...
    return parameters

### 常数 ###
layers_dims = [12288, 20, 7, 5, 1] #  4-layer model

# 梯度函数: L_layer_model

def L_layer_model(X, Y, layers_dims, learning_rate = 0.0075, num_iterations = 3000, print_cost=False):
    """
    实现L层神经网络：[线性->RELU]*（L-1）->线性->SIGMOID。
	参数：
	X—数据，形状的numpy数组（num_px*num_px*3，示例数）
	Y——真“标签”向量（如果是cat，则包含0，如果是非cat，则包含1），形状（1，示例数）
	layers\u dims—包含输入大小和每个层大小的列表，长度（层数+1）。
	学习率——梯度下降更新规则的学习率
	num_iterations—优化循环的迭代次数
	print\u cost—如果为真，则每100步打印一次成本
	退货：
	参数——模型学习的参数。然后可以用来预测。
    """

    np.random.seed(1)
    costs = []                         # 跟踪成本
    
    # 参数初始化。
    #(≈ 1行代码)
    # parameters = ...
    # 你的代码从这里开始
    parameters = initialize_parameters_deep(layers_dims)
    
    # 你的代码到此结束
    
    # 回路（梯度下降）
    for i in range(0, num_iterations):

        # 正向传播：[线性->RELU]*（L-1）->线性->SIGMOID。
        #(≈ 1行代码)
        # AL, caches = ...
        # 你的代码从这里开始
        AL, caches = L_model_forward(X, parameters)
        
        # 你的代码到此结束
        
        #计算成本。
        #(≈ 1行代码)
        # cost = ...
        # 你的代码从这里开始
        cost = compute_cost(AL, Y)
        
        # 你的代码到此结束
    
        # 反向传播。
        #(≈ 1行代码)
        # grads = ...    
        # 你的代码从这里开始
        grads = L_model_backward(AL, Y, caches)
        
        # 你的代码到此结束
 
        # 更新参数。
        #(≈ 1行代码)
        # parameters = ...
        # 你的代码从这里开始
        parameters = update_parameters(parameters, grads, learning_rate)
        
        # 你的代码到此结束
                
        # 每100次迭代打印一次成本
        if print_cost and i % 100 == 0 or i == num_iterations - 1:
            print("Cost after iteration {}: {}".format(i, np.squeeze(cost)))
        if i % 100 == 0 or i == num_iterations:
            costs.append(cost)
    
    return parameters, costs

测试运行：

parameters, costs = L_layer_model(train_x, train_y, layers_dims, num_iterations = 1, print_cost = False)

print("Cost after first iteration: " + str(costs[0]))

L_layer_model_test(L_layer_model)

运行结果：

Cost after iteration 0: 0.7717493284237686
Cost after first iteration: 0.7717493284237686
Cost after iteration 1: 0.7070709008912569
Cost after iteration 1: 0.7070709008912569
Cost after iteration 1: 0.7070709008912569
 All tests passed.

5.1-训练模型

如果您的代码通过了前一个单元，请运行下面的单元，将您的模型训练为4层神经网络。

-每次迭代的成本都应该降低。
-运行2500次迭代可能需要5分钟。

训练模型：

parameters, costs = L_layer_model(train_x, train_y, layers_dims, num_iterations = 2500, print_cost = True)

训练结果：

Cost after iteration 0: 0.7717493284237686
Cost after iteration 100: 0.6720534400822914
Cost after iteration 200: 0.6482632048575212
Cost after iteration 300: 0.6115068816101356
Cost after iteration 400: 0.5670473268366111
Cost after iteration 500: 0.5401376634547801
Cost after iteration 600: 0.5279299569455267
Cost after iteration 700: 0.4654773771766851
Cost after iteration 800: 0.369125852495928
Cost after iteration 900: 0.39174697434805344
Cost after iteration 1000: 0.31518698886006163
Cost after iteration 1100: 0.2726998441789385
Cost after iteration 1200: 0.23741853400268137
Cost after iteration 1300: 0.19960120532208644
Cost after iteration 1400: 0.18926300388463307
Cost after iteration 1500: 0.16118854665827753
Cost after iteration 1600: 0.14821389662363316
Cost after iteration 1700: 0.13777487812972944
Cost after iteration 1800: 0.1297401754919012
Cost after iteration 1900: 0.12122535068005211
Cost after iteration 2000: 0.11382060668633713
Cost after iteration 2100: 0.10783928526254133
Cost after iteration 2200: 0.10285466069352679
Cost after iteration 2300: 0.10089745445261786
Cost after iteration 2400: 0.09287821526472398
Cost after iteration 2499: 0.08843994344170202

训练集预测：

pred_train = predict(train_x, train_y, parameters)

效果：

Accuracy: 0.9856459330143539

测试集预测：

pred_test = predict(test_x, test_y, parameters)

预测结果：

Accuracy: 0.8

恭喜！在同一个测试集上，4层神经网络的性能（80%）似乎比2层神经网络（72%）更好。
这对于这项任务来说是相当好的表现。干得好！
在“改进深层神经网络”的下一个课程中，您将能够通过系统地搜索更好的超参数来获得更高的精度：例如，学习速率、层大小或数值迭代。

6-结果分析

首先，看一些L层模型标注错误的图片。这将显示一些错误标记的图像。

print_mislabeled_images(classes, test_x, test_y, pred_test)

有几种类型的图像模型往往表现不佳，包括：

猫的身体在一个不寻常的位置
猫出现在相似颜色的背景下
不寻常的猫的颜色和种类
摄像机角度
图片的亮度
比例变化（cat在图像中非常大或非常小）

恭喜你完成这项任务！
你刚刚建立并训练了一个深层的L层神经网络，并应用它来区分猫和非猫，这是深度学习中非常严肃和重要的任务
到目前为止，您已经完成了深度学习专业课程1的所有作业。太棒了！如果你想测试一下你自己和一只猫有多像，下面有一个可选的不分级练习，你可以测试一下你自己的形象。
干得好，希望下节课能见到你！

7-使用自己的图像进行测试（可选/未分级练习）

从这一点来说，如果您选择这样做，您可以使用自己的图像来测试模型的输出。为此，请执行以下步骤：

1.点击本笔记本上方栏中的“File”，然后点击“Open”进入Coursera Hub。
2.将您的图像添加到这个Jupyter笔记本的目录中，在“images”文件夹中
3.在以下代码中更改图像的名称
4.运行代码并检查算法是否正确（1=cat，0=non-cat）！

## 此处开始代码 ##
my_image = "my_image.jpg" # c将此更改为图像文件的名称
my_label_y = [1] # 图像的真实类（1->cat，0->non cat）
## 此处结束代码 ##

fname = "images/" + my_image
image = np.array(Image.open(fname).resize((num_px, num_px)))
plt.imshow(image)
image = image / 255.
image = image.reshape((1, num_px * num_px * 3)).T

my_predicted_image = predict(image, my_label_y, parameters)


print ("y = " + str(np.squeeze(my_predicted_image)) + ", your L-layer model predicts a \"" + classes[int(np.squeeze(my_predicted_image)),].decode("utf-8") +  "\" picture.")

运行结果：

y = 1.0, your L-layer model predicts a "cat" picture.