北大硕士LeetCode算法专题课-基础算法之排序

 接连上篇：北大硕士LeetCode算法专题课---算法复杂度介绍_骨灰级收藏家的博客-CSDN博客

冒泡排序

冒泡排序（Bubble Sort）是一种很原始的排序方法，就是通过不断地交换“大数”的位置达到排序的目的。 因为不断出现“大数”类似于水泡不断出现，因此被形象地称为冒泡算法。

冒泡算法的基本原理：比较相邻两个数字的大小。将两数中比较大的那个数交换到靠后的位置。

不断地交换下去就可以将最大的那个数放到队列的尾部。然后重头再次交换，直到将数列排成有序数列

以数列[5, 9, 3, 1, 2, 8, 4, 7, 6]为例，最初的数列顺序如上图所示

第一轮排序：按照冒泡排序的原理，比较相邻两个数字的大小。

从数列末端开始，第1次比较7和6的大小。7>6，交换7和6的位置。把较大的那个数7交换到靠后的位置。

第2次排序比较4和6的大小。6比4大，不需要交换位置

第3次排序比较8和4的大小。4比8小，交换4和8的位置位置 第4次排序比较2和4的大小。4比2大，不需要交换位置

第5次排序比较2和1的大小。2比1大，不需要交换位置

第6次排序比较1和3的大小。1比3小，交换1和3的位置 第7次排序比较1和9的大小。1比9小，交换1和9的位置 第8次排序比较1和5的大小。1比5小，交换1和5的位置

第一轮排序结束, 成功的将序列中最小的数1交换到了队列最前面。

第二轮排序：过程与前一轮类似，依然从末尾开始进行相邻两个元素的比较

当前面的元素比后面的元素大，交换两个元素的位置，第二轮排序只需要进行7次比较 经过第二轮排序后，数列中最小的两个元素已经交换到数列的最前面。

第三轮排序：依旧是回到数列的末尾，重新比较相邻的两个元素。

经过六次比较后，第三轮排序完成， 1,2,3三个最小的元素移动到了数列的头部

 

第四轮排序：经过五次比较，第四轮排序完成后，1,2,3,4四个最小的元素移动到了数列的头部。

完整的排序过程需要经过八轮比较(9个元素)，后四轮的排序过程与前面类似，经过八轮排序后，排序过程完成。 一个n个数的数列需要排序n-1轮。这样可以确保得到一个有序的数列。因此冒泡排序的时间复杂度是O(n2)。

冒泡排序代码

在写冒泡排序的代码前，先编写一段程序，创建无序数列，用于测试排序算法。 创建无序数列的程序randomList.py，代码如下： 

冒泡排序的程序bubbleSort.py的代码如下：

 

测试冒泡排序方法，代码如下：

 选择排序

与冒泡排序相比，选择排序算法（Selection Sort）的原理更加简单粗暴，就是在数列中不断地找最小（大）的那个数。

选择排序算法的基本原理：从数列中选择最大（最小）的那个数，将这个数放到合适的位置，然后在删除这个数的子数列

中选择最大（最小）的那个数，将这个数放到合适的位置……直到子数列为空。

 

以数列[6, 1, 7, 8, 9, 3, 5, 4, 2]为例，最初的数列顺序如上图所示

第一轮排序：以数列中第1个数为基数，遍历数列中其他的数字，找到最小的那个数，然后交换这两个数(6和1)的位置。

第二轮排序：以数列中第2个数为基数，遍历数列中其他的数字，找到最小的那个数(2)，然后交换这两个数(6和2)的位置。

第三轮排序：按照上面的规律，不断地找剩余数列中最小的数字，交换位置，直到将原始数列排成有序数列。

选择排序数列完毕。共9个数，排序8轮，时间复杂度是O(n2)。

选择排序的程序selectionSort.py的代码如下：

 测试选择排序方法，代码如下：

选择排序原理:

①不断将数列中的最小值交换到数列头部实现排序

② 选择排序的时间复杂度是O(n2)

插入排序

插入排序（Insertion Sort）很容易理解，插入排序方法与打扑克抓牌的排序很相似。在打扑克时，每抓一张新牌，

都会与手上已有的牌进行比较，将新牌插入到比自己小的牌后面。在取完所有的牌后，手上已有的牌就是个有序的序列。

插入排序原理：首先将数列分成两部分。数列的第一个数为left部分，其他的数为right部分。然后将right部分中的数逐一取出，

插入left部分中合适的位置。当right部分为空时，left部分就成为了一个有序数列

以数列[5, 3, 4, 7, 2, 8, 6, 9, 1]为例，最初的数列顺序如上图所示

第一轮排序：先将数列分成左、右两部分，左半部是第一个数字，右半部是数列剩余的部分。

第二轮排序：从右半部取出第一个元素3，与左半部的数字5比较，3比5小，放到5左边。

 第三轮排序：从右半部取出第一个元素4，与左半部的数字3、5比较，插入到合适的位置上。

第N轮排序：从右半部不断取出元素，与左半部的数字比较插入到左半部合适的位置上，直到所有数字完成排序。

 插入排序的程序insertionsort.py的代码如下：

插入排序的时间复杂度是O(n2)。

测试插入排序方法，代码如下：

 插入排序原理:

① 将数列分成两部分，数列的第一个数为left部分，其他的数为right部分

② 将right部分中的数逐一取出，插入left部分中合适 的位置

归并排序

归并排序（Merge Sort）是一种典型的递归法排序。它把复杂的排序过程分解成一个简单的合并子序列的过程。

归并排序原理：先将数列分成左右两份（最好是等分），然后将左、右子数列排序完毕后再合并到一起就成了一个有序数列

左、右两个子数列变成有序数列的过程是一个递归过程：再把子数列分成左、右两份，把子子数列排序完毕后合并成子数列…

 

 以数列[6, 4, 3, 7, 5, 1, 2]为例，最初的数列顺序如上图所示

第一次分组：先将数列分成左、右两部分，此时左边4个元素右边3个元素，也不是有序数列，不能合并。

第二次分组：继续分解子数列，分组后子子序列中还有长度为2的数列，无法确定长度为2的数列是否有序，还需继续分组

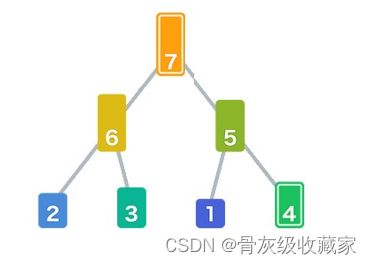
第一次合并：经过三次分组，所有的子子子数列都为长度为1的数列。开始合并，将两个有序子数列合并成一个新的有序序列。

第二次合并：将4个子子数列合并成两个子数列，合并后两个子数列均为有序数列。

第三次合并：将剩余的数列合并到一个数列中。归并排序完毕。经过3次合并，最终得到了一个有序数列。 归并排序的时间复杂度是O(nLogn)

 

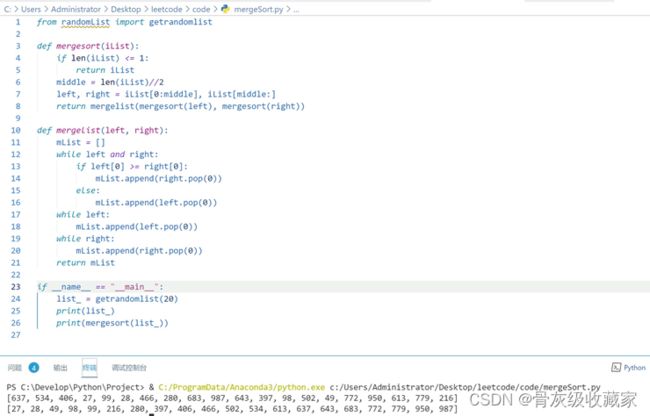
测试插入排序方法，代码如下：

 归并排序原理:

① 将数列不断分成两组直到不能再分，在合并时排序

② 归并排序的时间复杂度是O(nlogn)

快速排序

快速排序（Insertion Sort）也是一种递归排序算法。

快速排序原理：先以列表中的任意一个数为基准（一般选头或尾），将列表分为左、右两个子列表：

左子列表的数要比基准数小，右子列表的数要比基准数大。然后继续把左子列表和右子列表按同样的方法继续分解、

比较，直到分无可分。最后将左子列表（比基准数小）+基准数+右子列表（比基准数大）连接起来得到一个有序数列。

以数列[3, 5, 8, 1, 2, 9, 4, 7, 6]为例，最初的数列顺序如上图所示

第一次分组：以最后一个元素6为基准将数列分成两组。分别从左右两端遍历数列，比6小的分在左边，比6大的分在右边。 先从左向右遍历， 当遇到比6大的元素时将该元素放到右边。同理从右向左遍历时，遇到比6小的元素放到左边。

当全部元素被遍历之后，将左边数列，元素6，右边数列按顺序拼接成新的数组，此时元素6的位置固定。

递归处理左边子数列：以最后一个元素2为基准，比2小的分在左边子数列中，比2大的分在右边子数列中 经过一轮分组后，元素2的位置已经固定，接下来继续递归的调用上述过程……

 

递归处理右边子数列：以最后一个元素9为基准，比9小的分在左边子数列中，比9大的分在右边子数列中 经过一轮分组后，只会分成一组【8，7】，再次递归处理【8，7】，至此排序完毕

 

快速排序的程序quicksort.py的代码如下：

 

测试快速排序方法，代码如下：

 快速排序原理:

①不断将数列中的最小值交换到数列头部实现排序

② 快速排序的时间复杂度是O(n2)

计数排序

计数排序（Counting Sort）是一种稳定的线性时间排序算法。该算法于1954年由 Harold H. Seward 提出。

计数排序使用一个额外的数组C ，其中第i个元素是待排序数组A中值等于i的元素的个数。 然后根据数组C 来将A中的元素排到正确的位置

算法的步骤如下：

① 找出待排序的数组中最大和最小的元素, 创建从min, 到max的连续数组, 并赋初始值为0

② 统计数组中每个值为i的元素出现的次数，存入数组C 的第i项

 

 ③ 对所有的计数累加（从C 中的第一个元素开始，每一项和前一项相加）

 

④ 反向填充目标数组：将每个元素i放在新数组的第C[i]项，每放一个元素就将C[i]减去1以第一个元素4 为例, 4-1 = 3 在下面的计数数组中找到下标3对应的数据为6, 在新数组的6-1=5 的位置上填充4

 

 计数排序代码

时间复杂度: O(n+k)

计数排序原理:

① 找出待排序的数组中最大和最小的元素

② 统计数组中每个值为i的元素出现次数，存入数组C  的第i项

③ 对所有的计数累加（从C中的第一个元素开始，每 一项和前一项相加）

④反向填充目标数组：将每个元素ii放在新数组的第C[i]项，每放一个元素就将C[i]减去1

堆排序 

堆排序（Heap Sort）是利用堆数据结构进行排序的算法

堆排序原理：首先利用待排序数列构建最大堆（根节点保存最大值，父节点数据>子节点数据）,  接下来取出堆结构中的根节点元素，即为最大值，保存到新列表的末尾。

更新剩下的数据， 组成新的最大堆，并取出根节点元素（最大值），如此不断重复直到堆中的所有数据都被取出，排序完成

以数列[5, 2, 7, 3, 6, 1, 4]为例，最初的数列顺序如上图所示

构建最大堆：最大堆属于二叉堆的一种，父结点的元素总是大于或等于任何一个子节点的元素；在最大堆中任意子堆都满足 父结点的元素总是大于或等于任何一个子节点的元素这一性质。

数列中所有的元素已经存储到最大堆中。

从最大堆中取出根节点元素：根节点元素是堆中的最大值，每取出一个元素便重新调整堆的结构，保证根节点的元素为剩 下元素中的最大值。这样依次将所有元素取出，即完成排序。

 

堆排序的程序heapsort.py的代码如下：

 

 堆排序原理:

①构建最大二叉堆，不断从堆顶取出元素，完成排序

② 堆排序的时间复杂度是O(nlogn)