ML - SVM 支持向量机
文章目录
-
- 什么是 SVM
-
- 不适定问题
- Hard & Soft Margin SVM
- Hard Margin SVM 的数学思想及求解
- Soft Margin 和 SVM 的正则化
- 核函数
-
- 多项式核函数
- 高斯核函数
- SVM 解决回归问题
什么是 SVM
SVM : Support Vector Machine
既可以解决分类问题,也可以解决回归问题
不适定问题
逻辑回归是找到了决策便捷;
问题:对于一些数据,决策边界并不唯一。这个问题也叫 不适定问题。
逻辑回归解决上述问题的方法:定义了一个概率函数(sigmoid),根据概率函数建模 形成了损失函数;最小化损失函数,从而求出一条决策边界。
这的损失函数是由 训练数据集 决定的。
上述方法可能存在泛化问题:这个决策边界,对于没有看到的数据,算不算好的决策边界呢?
SVM 期望 找到的决策边界 泛化能力尽可能的好,没有寄望在数据的预处理阶段 或 对模型的正则化方式,而是将对泛化能力的考量 放在算法内部。让决策边界 离 分类样本 都尽可能的远。
这个理论也有他的数学理论。SVM 也用于统计学。
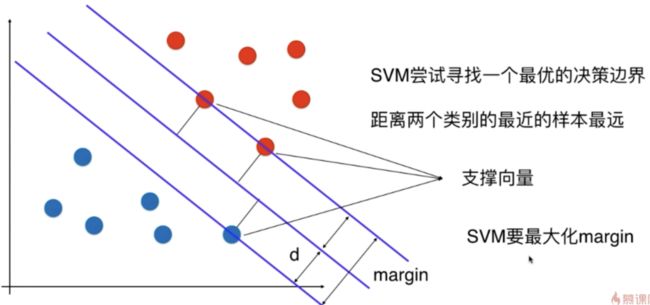
尽可能的远
这两个直线 和 决策边界平行,定义了一个区域;在这个区域内都没有任何数据点。
SVM 最终得到的 决策边界 就相当于这个区域 中间的那根线。
这些最近的点,称为 支撑向量。
SVM 是要最大化 margin;
Hard & Soft Margin SVM
以上算法是对于线性可分的问题,就是存在一根直线,或者一个超平面 可以将这些点划分;这样算法也称为 Hard Margin SVM,非常严格。
真实情况下的数据是 线性不可分的,通过对 SVM 改进得到 Soft Margin SVM。
Hard Margin SVM 的数学思想及求解
点到直线的距离
(x, y) 到 Ax + By + C = 0 的距离: A x + B y + C A 2 + B 2 \frac{ Ax + By + C } { \sqrt{ A^2 + B^2 } } A2+B2Ax+By+C
为什么不使用 y = kx + b
Ax + By + C = 0 是解析几何形式的方程;必须要求这个直线不能和 X轴垂直(不能和Y轴平行),y = kx + b 这种形式的直线方程有局限性,无法表达 k 是正无穷。
距离公式拓展到 n 维空间,直线表达为 $ \theta^T x_b = 0 $ --> $ w^T + b = 0 $
w:weight 权值
b:截距
任意一点到这条直线的距离: ∣ w T + b ∣ ∣ ∣ w ∣ ∣ \frac{ | w^T + b | }{ ||w|| } ∣∣w∣∣∣wT+b∣
∣ ∣ w ∣ ∣ = w 1 2 + w 2 2 + . . . + w n 2 ||w|| = \sqrt{ w_1^2 + w_2^2 + ... + w_n^2 } ∣∣w∣∣=w12+w22+...+wn2
最优化目标函数: m i n 1 2 ∣ ∣ w ∣ ∣ 2 min \frac{1}{2} ||w||^2 min21∣∣w∣∣2
限定条件:数据满足 s . t . y ( i ) ( w T x ( i ) + b ) > = 1 s.t. y^{(i)} (w^T x^{(i)} + b ) >= 1 s.t.y(i)(wTx(i)+b)>=1
之前的最优化问题都是无条件的,也称为 全局最优化问题;这里是 有条件的最优化问题,求解方法更复杂,要使用到 拉普拉斯求解。
Soft Margin 和 SVM 的正则化
以上介绍的是线性 SVM
核函数
对于复杂的变形,使用核函数计算量会变小,还回节省存储空间。
核函数不是 SVM 专用,只是在 SVM 中较多使用。
多项式核函数
多项式核函数 K ( x , y ) = ( x ⋅ y + c ) 2 K(x, y) = ( x \cdot y + c )^2 K(x,y)=(x⋅y+c)2
线性核函数 K ( x , y ) = x ⋅ y K(x, y) = x \cdot y K(x,y)=x⋅y
高斯核函数
也称为 RBF 核:Radial Basis Function Kernel,径向基函数
是 SVM 中使用最多的算法;
K(x, y) 表示 x 和 y 的点乘;
K ( x , y ) = e − γ ∣ ∣ x − y ∣ ∣ 2 K(x, y) = e^{-\gamma || x - y ||^2 } K(x,y)=e−γ∣∣x−y∣∣2
对于高斯核函数,只有一个超参数: γ \gamma γ
高斯核函数的本质,是将每一个样本点 映射到一个 无穷维的特征空间。
对于每一个数据点 都是 landmark, mn 的数据映射成了 mm 的数据。
适用于 数据纬度高,数据量少。比如 自然语言处理。
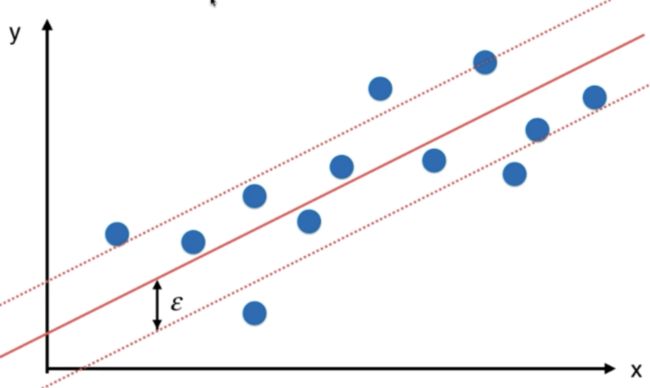
SVM 解决回归问题
怎样定义拟合,是不同回归算法的关键。
线性回归中,希望 MSE 最小。
SVM 中指定margin值,期望 margin 范围中包含的数据越多越好。(和分类相反)
引入超参数 ϵ \epsilon ϵ