带权并查集 详解

简介

带权并查集与普通并查集的区别在于，其每条边/每个点都有权值。因此，我们需要额外用一个数组来维护每个点 $x$ 到其当前祖先 $f{a}_x$ 的权值和，并在路径压缩的时候维护。

直接说可能较难理解，于是下面是一道例题。

P1169

Description

传送门

Solution

考虑对于每个点 $x$，维护其到其祖先 $f{a}_x$ 的距离 $de{p}_x$，并对于每个并查集的根维护连通块大小 $siz$。

对于一个 M 操作，令涉及到的战舰分别为 $x,y$，我们找到 $x$ 的祖先 $fx$ 以及 $y$ 的祖先 $fy$。然后，我们更新 $f{a}_{fx}:=fy$ 以及 $de{p}_{fx}:=si{z}_{fy},si{z}_{fy}:=si{z}_{fy}+si{z}_{fx}$。

对于一个 C 操作，我们先判断 $fx$ 是否与 $fy$ 相等。若不相等，则输出 $-1$；否则答案是 $|de{p}_{fx}-de{p}_{fy}|-1$。

这样本题是否就被解决了呢？如果你足够细心，你会发现: 在一次 M 操作过后，$fx$ 的 $dep$ 以及 $fa$ 产生了变化，而这会导致整棵以 $fx$ 为根的子树的 $dep,fa$ 产生变化，然而我们并没有更新 $\cdots \cdots$

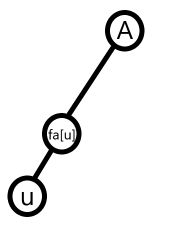
其实并没有关系。当我们查询某个节点 $u$ 的信息的时候，我们并不直接查询 $de{p}_u$，而是先对 $u$ 进行路径压缩，并在路径压缩的过程中更新信息，最后再查询 $de{p}_u$。具体来说，在路径压缩的过程中，我们先求出 $u$ 的祖先 $A$，然后执行 $de{p}_u:=de{p}_u+de{p}_{f{a}_u}$（注意这里是 $f{a}_u$ 而不是 $A$），并在回溯的时候令 $f{a}_u=A$。

int Find(int u){
	if (u==fa[u])  return u;
	
	int A=Find(fa[u]);
	dep[u]+=dep[fa[u]];
	return (fa[u]=A);
}

其中 $de{p}_u:=de{p}_u+de{p}_{f{a}_u}$ 的实际意义如下：

原来 $de{p}_u$ 维护的是从 $u$ 到 $f{a}_u$ 的距离，而现在需要将其改为从 $u$ 到 $A$ 的距离。显然，从 $u$ 到 $A$ 的距离，就是从 $u$ 到 $f{a}_u$ 的距离加上从 $f{a}_u$ 到 $A$ 的距离。因此，$de{p}_u$ 的新值应该是 $de{p}_u+de{p}_{f{a}_u}$。注意，此时 $de{p}_{f{a}_u}$ 已经被更新过。

Code

const int maxl=30005;
int t,n,x,y;char opt;
int fa[maxl],dep[maxl],siz[maxl];

int Find(int x){
	if (x==fa[x])  return x;
	
	int new_fa=Find(fa[x]);
	dep[x]+=dep[fa[x]];
	return fa[x]=new_fa;
}

signed main(){
	t=read(),n=30000;
	for (int i=1;i<=n;i++)  fa[i]=i,siz[i]=1;
	
	while (t--){
		cin>>opt;x=read(),y=read();
		if (opt=='M'){
			int fx=Find(x),fy=Find(y);
			fa[fx]=fy;
			dep[fx]+=siz[fy];
			siz[fy]+=siz[fx];
		}
		else{
			int fx=Find(x),fy=Find(y);
			if (fx!=fy)  puts("-1");
			else printf("%d\n",abs(dep[x]-dep[y])-1);
		}
	}
	return 0;
}

带权并查集的其他应用

其实，带权并查集就是一个非常套路的东西。只要摸清楚了其本质就不难了。

下面是找来的几个题，可以写一写提升自己对带权并查集的熟练度。

LNR #1 D1T2
P3733